

Up: Mass determination of
In this section we introduce the orbital motion of the components and its
observational consequences.
During the 37 months of the mission, each program star has been observed at about 30
epochs, over different scanning directions. If the orbital period is
large in comparison to the mission length, the displacement of the photocentre and of
the centre of mass is just an uniform proper motion. However the hippacentre would
sway in the vicinity of the photocentre with the changing scanning direction and
a careful examination of the residuals could inform that the source is not a
single star. Nevertheless, for most of those stars, the result would show up as an
increase of the unit weight variance derived from the fit of the observations to
the astrometric model.

Figure 4: Paths of the components of a double star around the centre of mass G,
during an orbital period of nearly 3 years. a, e and B are resp.
the semi-major axis, the eccentricity, and the mass fraction. About 30 observations were simulated,
each one yielding to an hippacentre H, represented by the vertices of the dotted
broken line. In this case, the position of H lies between the
photocentric ellipse and the line of the
outer hippacentre 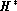 , which would occur if the projection of
the double star's separation on the grid were always at its maximum. In the periastron
vicinity, H and F are no longer distinct
, which would occur if the projection of
the double star's separation on the grid were always at its maximum. In the periastron
vicinity, H and F are no longer distinct
The existence of a significant orbital motion over the duration of the mission has at
least two consequences:

- The projection of the double star on
the grid depends on both the scanning angle of the circle and the parameters
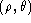 of the binary at the time when the observations took place. Thus, the
distribution of these projections is not only due to the satellite's scanning law
(which depends strongly on the ecliptic latitude of the object).
of the binary at the time when the observations took place. Thus, the
distribution of these projections is not only due to the satellite's scanning law
(which depends strongly on the ecliptic latitude of the object).

- The separation
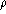 of the pair is a function of time; the
amplitude of variation depends on the eccentricity of the true orbit and on its
orientation with respect to the tangential plane of the celestial sphere. As a
result, even if the semi-major axis is sufficiently large, the
distinction between the hippacentre
(H) and the photocentre
(F) may not be possible all along the orbit. However from the second Kepler's law,
most of the orbital period is spent in the apoastron region rather than in the
periastron, a circumstance which is much favourable to the detection.
of the pair is a function of time; the
amplitude of variation depends on the eccentricity of the true orbit and on its
orientation with respect to the tangential plane of the celestial sphere. As a
result, even if the semi-major axis is sufficiently large, the
distinction between the hippacentre
(H) and the photocentre
(F) may not be possible all along the orbit. However from the second Kepler's law,
most of the orbital period is spent in the apoastron region rather than in the
periastron, a circumstance which is much favourable to the detection.
In order to see the distribution of a typical set of observations of an
orbital binary, we have simulated the phenomenon for various orbital parameters and
with a real sequence of observations over the 37 months of the mission. The results
are plotted in Figs. 4 (click here)-5 (click here) for three values of the semi-major axis, assuming an
orbital plane perpendicular to the line of sight. The absolute
paths of the components and of the photocentre are represented. The vertices of the
broken lines indicate where the hippacentres lay during these observations.
The additional curve labeled 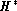 corresponds to the
path that the hippacentre would have followed had the scanning direction of the
satellite been always parallel to the line defined by the two components. This
virtual point is noted
corresponds to the
path that the hippacentre would have followed had the scanning direction of the
satellite been always parallel to the line defined by the two components. This
virtual point is noted 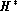 and called outer hippacentre. One must stress
that the line of
and called outer hippacentre. One must stress
that the line of 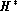 is not an ellipse, and in any case never similar to the
orbital paths of the components or of the photocentre. In the case of the binary star
appearing in Fig. 4 (click here), the hippacentre is restricted to move between
is not an ellipse, and in any case never similar to the
orbital paths of the components or of the photocentre. In the case of the binary star
appearing in Fig. 4 (click here), the hippacentre is restricted to move between
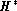 and the photocentre's and to lie between the primary and the photocentre. For
separations larger than half the gridstep, this property is no longer true, as shown
in Fig. 5 (click here)b. These cases illustrate two of the many other simulations with
different values of the semi-major axis
a, the eccentricity e, the magnitude difference
and the photocentre's and to lie between the primary and the photocentre. For
separations larger than half the gridstep, this property is no longer true, as shown
in Fig. 5 (click here)b. These cases illustrate two of the many other simulations with
different values of the semi-major axis
a, the eccentricity e, the magnitude difference 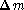 and the mass fraction
B, carried out in order to get a better understanding of the behaviour of the
hippacentre. The path of the secondary is not represented for the sake of clarity.
and the mass fraction
B, carried out in order to get a better understanding of the behaviour of the
hippacentre. The path of the secondary is not represented for the sake of clarity.
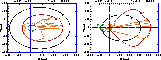
Figure 5: a and b) Two different configurations of short-period binaries. The origin
is the centre of mass. We can see in both cases the non-elliptical shape
of the path of the outer hippacentre 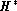 . This path cannot be obtained from the
photocentre by a simple dilatation
. This path cannot be obtained from the
photocentre by a simple dilatation


Up: Mass determination of
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr

