The basic Hipparcos
signal records during the transit of a star on the grid is modelled as the sum of
two harmonics (Murray et al. 1989) as,
where I is the total intensity, B the unmodulated background,
M and N respectively the modulation coefficients of the first and second harmonic
and
and 
the corresponding phases.
For a single star the additional relationship 
holds, and the value
of the phase is directly linked to the direction of the star, that is to say to the
photocentre of the light source.
As a result of the linearity of the Hipparcos detector, when two or more star images are simultaneously on the sensitive part of the detector their contributions add linearly and the resulting signal has exactly the same form as Eq. (1), but without the simple link between the two phases.
The positional information contained in the phase 
(indeed, we consider in the actual
implementation the combination of 
and 
into a single weighted phase, but as far as the
principles are concerned, this is not essential) must be related to the relative
position and relative luminosity of the components. If 
are the
intensities of the bright and faint component we introduce the fraction 
and the phase difference between the secondary and primary as
(also noted 
in Mignard et al. 1995).
A simple algebraic computation gives (Mignard et al. 1989, 1995),
where the Angle function is defined as follows:
where r is the modulus 
.
The intensity fraction 
is related to the magnitude difference by:
What matters now is the difference between the observed phase 
of the
hippacentre and that of the primary or that of the photocentre. For the sake of
simplicity consider the two stars with separation 
crossing the grid in such a
way that the line between the two components is perpendicular to the slits of the grid.
In this case one has 
where s is the gridstep of
Hipparcos of size 1
208. For 
one has 
, 
and 
, which yields with
Eq. (2),
which is nothing but the phase of the photocentre, since 
. Thus in the limit of
small separations, the hippacentre and the photocentre are alike. It is obvious
from Eq. 2, that this situation does not hold true for any separation. For larger
separations we have to the third order in 
,
which may be larger than 10 mas for 
. The difference is noticeable
to Hipparcos.
Therefore, while an observation of an unresolved binary with the classical means is tied to the photocentre, the physical point (referred to as the hippacentre) attached to an Hipparcos observation of a close binary star is a point lying on the direction defined by the two components, generally between the primary and the photocentre (in some cases, the hippacentre may lie outside the segment joining the components, in the vicinity of the primary). Unlike the photocentre, the distance between the primary and the hippacentre is not a simple linear function of the separation. This will proved crucial in interpreting the path of the hippacentre on the sky induced by the orbital motion.
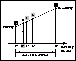
Figure 1: Principle of the projection on the
scanning circle of the points characterizing a double star. The
hippacentre H' is defined on the grid but can be linked to a point H
on the sky. Its position with respect to the components is however variable
from an observation to the other
. More important, its relative position with respect to P, S and F, as shown in Fig. 2 (click here),
changes from one observation to another as a result of the scanning direction and the
non-linearity of Eq. (2), which is not true for the photocentre.
Let
be the vector 
oriented from the primary to the secondary. The positions of the centre of mass
and of the photocentre are respectively given by,
where 
is the total mass of the system.
With
and B being respectively the intensity and mass fractions 
and
we have for the position of the photocentre with respect
to the centre of mass and its
grid counterpart:
which shows that the projected distance depends on 
and B only through the
difference (
). The corresponding equations for the hippacentre
H read:
For small separations 
, (Eq. 4) and there is no
difference between an Hipparcos observation and the classical observation of the
photocentre of an unresolved system. For larger separations the actual position of
H depends separately on the mass ratio and the intensity ratio and on the
scanning direction, which was perfectly known in all the Hipparcos observations.
Equation (5) is related to the astrographic observations of the absolute motion of the
primary of a wide pair over a long period of time. From the motion of the primary
with respect to the stellar environment, one can fit by the method of least square,
the two angular coordinates of the centre of mass, the two components of the proper
motion, the parallax and 
.
Equation (6)
is the basic relationship used in the analysis of the absolute motion of
the photocenter of an unresolved astrometric binary. It shows that the
photocentric orbit has the same shape as the relative orbit with a scale
defined by 
. When 
, one recovers the extreme
case of a binary with an unseen companion, first investigated by Bessel in
the mid 19th century. In this case the photocentre and the primary coincide.
Finally, Eq. (7) relates the hippacentre to the centre of mass in more or less the same way as Eq. (6) links the photocentre to the center of mass. A fit of absolute observations carried out over a duration comparable to the orbital period will lead to the simulataneous determination of the astrometry of the centre of mass and the physical parameters concealed in the scale coefficient.
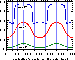
Figure 2: Behaviour of the ratio 
as a function of the angle between the scanning
direction and that defined by the two components, for three different values of the magnitude
difference. The binary is supposed to be fix on the sky and its separation is 
. It
shows that, unlike the photocentre, the position of the hippacentre with respect to the components may
be highly variable from an observation to the other
Equation (7) shows that the distance between the hippacentre and the centre of
mass generally includes information on the physical parameters 
and B
separately of one another. This very interesting feature is no longer true in
three particular configurations:
. For a
binary star with a given global magnitude
, there is a threshold in separation below which we cannot distinguish the
hippacentre from the photocentre.
Taking a detection criterion of 
, where 
is the standard error
of the estimation of the position of the hippacentre on the grid, the limits are
plotted in Fig. 3 (click here), as a function of the magnitude difference 
. The curves
are representative of the standard error for stars of magnitude 
and
the distinction is not feasible below a particular line. From Fig. 3 (click here) one can set a
broad limit of about 
arcsec. These values will be made more
precise in Sect. 5 on the basis of an extensive simulation taking account of the
different steps of the processing.
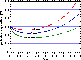
Figure 3: Limit in separations projected on the grid, beyond which the
hippacentre becomes recognizable from the photocentre, as a function of the
magnitude difference and of the measurement error. The three values of 
chosen here correspond to an Hipparcos magnitude of nearly 2, 10 and 12 mag for
the system
. In this case, we have
. The ratio 
is then equal to 
, which
means that once again, the distance between the hippacentre and the photocentre is
hardly discernible. However, with the use of the phase 
of the second harmonic, it can be shown
that for projected separations larger than 0.25 gridstep (or equivalently about 0
3 on the sky),
the hippacentre and photocentre become clearly distinct.
. The photocentre and the hippacentre are both
very close to the primary and thus close to one another. In
the extreme case when the companion is invisible by Hipparcos (binary with an
unseen companion), the three points mix together.
In practical situations, the first limitation remains the most important, as long a it precludes any separate determination of the mass and intensity ratio.
If the semi-major axis is
large enough to yield separations on the sky larger than the limit appearing in
Fig. 3 (click here), when 
, the set of observations should contain some
favourable configurations of projection on the grid, allowing the hippacentre to be
sometimes distinct from the photocentre.
In the third case, when the companion is unseen, the information on the
value of 
is so strong (
) that the mass fraction B may easily
be derived (the phase 
is then equal to zero in any case of projection).