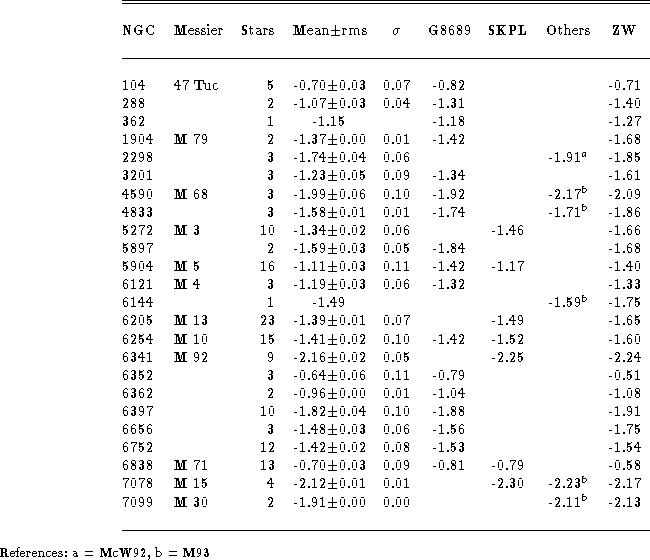
Table 8: Mean metallicities for globular clusters compared to literature data
Mean values of the metallicities derived for the 21 clusters analyzed are listed in Table 8 (click here).

Table 8: Mean metallicities for globular clusters compared to literature
data
The internal uncertainty in [Fe/H] abundances (![]() , where N is
the number of stars studied in each cluster) is very small: on average,
0.06 dex, which can be interpreted also as the mean precision of the cluster
ranking on our new metallicity scale. For comparison, in the same Table, we
also give the original [Fe/H] ratios obtained in previous analyses. In the
last column the metal abundances from the compilation of Zinn &
West (1984) are listed, superseded and integrated for a few clusters by
the new measurements
of Armandroff & Zinn (1988); this scale will be indicated as a whole,
hereinafter, as ZW.
, where N is
the number of stars studied in each cluster) is very small: on average,
0.06 dex, which can be interpreted also as the mean precision of the cluster
ranking on our new metallicity scale. For comparison, in the same Table, we
also give the original [Fe/H] ratios obtained in previous analyses. In the
last column the metal abundances from the compilation of Zinn &
West (1984) are listed, superseded and integrated for a few clusters by
the new measurements
of Armandroff & Zinn (1988); this scale will be indicated as a whole,
hereinafter, as ZW.
The 24 clusters of Table 8 (click here) can now be regarded as standard
reference clusters to calibrate individual metal abundance indicators with
metallicities directly derived from high-dispersion spectroscopic analysis. We
feel confident that our list covers fairly well the whole range in metallicity
of globular clusters, going from typical metal-rich clusters, as 47 Tuc, M
71 and NGC 6352, to the classical metal-poor templates (M 92, M 15, M 68). The
sample of intermediate metallicity clusters is also very well represented among
our calibrators.
One
of our main purposes is to revise and refine the calibration of the ZW ranking
system, which covers almost all known globular
clusters. The main advantage of the ZW scale is that their system is applicable
even to the most distant objects, being based on the integrated parameter
![]() and/or on low-dispersion spectroscopy of the infrared Ca II triplet.
On the other side, any integrated index is not, by definition, a function of a
single element in a globular cluster. In particular, the major contribution to
line blanketing in the spectral range covered by the
and/or on low-dispersion spectroscopy of the infrared Ca II triplet.
On the other side, any integrated index is not, by definition, a function of a
single element in a globular cluster. In particular, the major contribution to
line blanketing in the spectral range covered by the ![]() index is due to
the H and K lines of Ca II, with other significant fractions due to the
index is due to
the H and K lines of Ca II, with other significant fractions due to the
![]() 3883 CN band and some Fe blends. Hence, reliability of ZW
metallicities ultimately rests on the coupling between Ca, C, N, and Fe
abundances. It is outside the purposes of this paper to
proceed further on this point;
we only wish to recall here that the strength of CN-bands is known to vary from star
to star (the so-called CN-signature), having a bimodal distribution in most
(but not all!) clusters (see Kraft 1994 for a recent review).
3883 CN band and some Fe blends. Hence, reliability of ZW
metallicities ultimately rests on the coupling between Ca, C, N, and Fe
abundances. It is outside the purposes of this paper to
proceed further on this point;
we only wish to recall here that the strength of CN-bands is known to vary from star
to star (the so-called CN-signature), having a bimodal distribution in most
(but not all!) clusters (see Kraft 1994 for a recent review).
Moreover (see e.g., Clementini et al. 1995, Sect. 5.1.1) the [Ca/Fe]
ratio does not scale with Fe on the whole range of metallicities, being lower
in metal-rich than in metal-poor Population II stars. Furthermore, a serious
caveat has been advanced on the claimed independence of the ![]() \
index from the horizontal branch morphology (see e.g., Smith 1984).
To overcome this kind of problems, the most straightforward way to correct
the ZW scale consists in working directly on the final
metallicities, since the original compilation of Zinn & West (1984) was
obtained averaging a number of [Fe/H] values derived from different indicators
(e.g.,
\
index from the horizontal branch morphology (see e.g., Smith 1984).
To overcome this kind of problems, the most straightforward way to correct
the ZW scale consists in working directly on the final
metallicities, since the original compilation of Zinn & West (1984) was
obtained averaging a number of [Fe/H] values derived from different indicators
(e.g., ![]() ,
, ![]() ,
, ![]() ) and calibrated against
) and calibrated against
![]() .
.
In Fig. 5 (click here) we then compare our high-dispersion [Fe/H] values with
the ZW values for the 24 calibrating clusters. The error bars (1 ![]() ) are
from Zinn & West (1984: Table 5) and from our Table 8 (click here).
As it is evident from this figure, the ZW scale is far from linear, deviating
both in the low and in the high metallicity regimes, when compared with [Fe/H]
from our direct analysis. In the
metal-rich region ([Fe/H]>-1) ZW's metallicities are on average 0.08 dex too
high for the 3 clusters 47 Tuc, M 71 and NGC 6352, with the last two objects
being responsible for most of the discrepancy (0.12 and 0.13 dex,
respectively). For
) are
from Zinn & West (1984: Table 5) and from our Table 8 (click here).
As it is evident from this figure, the ZW scale is far from linear, deviating
both in the low and in the high metallicity regimes, when compared with [Fe/H]
from our direct analysis. In the
metal-rich region ([Fe/H]>-1) ZW's metallicities are on average 0.08 dex too
high for the 3 clusters 47 Tuc, M 71 and NGC 6352, with the last two objects
being responsible for most of the discrepancy (0.12 and 0.13 dex,
respectively). For ![]() [Fe/H]
[Fe/H]![]() the [Fe/H] values of ZW are
definitively too low by a mean value of 0.23 dex (
the [Fe/H] values of ZW are
definitively too low by a mean value of 0.23 dex (![]() =0.09 dex, 16
clusters). Finally, in the very low-metallicity tail, ZW's values are on
average 0.11 dex higher than ours (
=0.09 dex, 16
clusters). Finally, in the very low-metallicity tail, ZW's values are on
average 0.11 dex higher than ours (![]() =0.06 dex, 6 clusters).
=0.06 dex, 6 clusters).
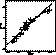
Figure 5: Mean metallicities for the 24 clusters from the present work
compared with metallicities on the Zinn & West scale (1984)
The non-linear behaviour has
been confirmed by a t-test on the significance of the quadratic term in the
relation between ZW and ours [Fe/H]'s.
To bring ZW's [Fe/H] ratios on a metallicity scale fully based only on high
dispersion spectroscopy (HDS) we then derived a correction given by a quadratic
relation. This procedure automatically takes into account also the different
zero point between the two scales, since the ZW scale was ultimately based on
the Cohen (1983) scale, which, as other past analysis, adopts the
traditional old solar Fe abundance log
![]() =7.67. The resulting function we derive for
this correction is:
=7.67. The resulting function we derive for
this correction is:
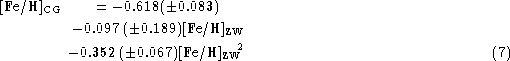
with the correlation coefficient r=0.982 and ![]() =0.08 for 24 clusters.
This relationship is highly significant, from a statistical point of view, and
can be applied to ZW metallicities in the range -2.24<[Fe/H]
=0.08 for 24 clusters.
This relationship is highly significant, from a statistical point of view, and
can be applied to ZW metallicities in the range -2.24<[Fe/H]![]() ,
defined by the lowest and highest values of [Fe/H]
,
defined by the lowest and highest values of [Fe/H]![]() among the
clusters used for the calibration. The quadratic regression line is shown as a
heavy line in Fig. 5 (click here); overimposed in the same figure is also the
result of a linear fit, which takes into account the errors. As one can see,
even considering 3
among the
clusters used for the calibration. The quadratic regression line is shown as a
heavy line in Fig. 5 (click here); overimposed in the same figure is also the
result of a linear fit, which takes into account the errors. As one can see,
even considering 3![]() error bars, it it very difficult to represent the
data on a linear scale, in particular at the lower metallicity edge.
error bars, it it very difficult to represent the
data on a linear scale, in particular at the lower metallicity edge.
Once the correction is applied the non-linearity of the ZW scale obviously disappears. However, a certain amount of scatter is still present in the intermediate-metallicity regime; we believe that it could be attributed to a residual effect, not well removed by our calibration, of the second parameter. This last is in fact likely to affect ZW's metallicities more severely in this regime, in which the integrated colours of clusters of different HB morphological type can be sensibly misinterpreted in terms of [Fe/H].
The next logical step would be now to calibrate other empirical metallicity
indicators, i.e. repeat the original work of Zinn & West (1984) but
using now our direct [Fe/H] values from HDS as a calibrating sequence.
The most interesting and accessible parameters are the photometric ones (e.g.,
![]() ,
, ![]() , etc.): they are widely used since it is easy
enough to measure them from the recent and accurate CCD-based colour-magnitude
diagrams (CMD). However, it would be preferable
to have a dataset of homogeneity and accuracy comparable
with the precision of our metallicities, instead of relying on compilation
from different sources.
Since such an effort is presently in progress on a
set of CMDs analyzed in a self-consistent way, we postpone to a forthcoming
paper this kind of calibration.
However, an immediate and meaningful comparison can be made with
the metallicity scale for globular clusters derived from RR Lyraes, since
we can compare results obtained for two different stellar populations, RGB
stars and HB stars, independently checking the validity of both scales.
, etc.): they are widely used since it is easy
enough to measure them from the recent and accurate CCD-based colour-magnitude
diagrams (CMD). However, it would be preferable
to have a dataset of homogeneity and accuracy comparable
with the precision of our metallicities, instead of relying on compilation
from different sources.
Since such an effort is presently in progress on a
set of CMDs analyzed in a self-consistent way, we postpone to a forthcoming
paper this kind of calibration.
However, an immediate and meaningful comparison can be made with
the metallicity scale for globular clusters derived from RR Lyraes, since
we can compare results obtained for two different stellar populations, RGB
stars and HB stars, independently checking the validity of both scales.
The most recent calibration of [Fe/H] in terms of the Preston's (1959)
index ![]() is the one
defined by Clementini et al. (1995), who found
is the one
defined by Clementini et al. (1995), who found
![]()
This relation was derived using RR Lyraes both in the field and in globular
clusters.
However, while metallicity values for field RR Lyraes were directly derived
from high-resolution spectra or from the re-analysis of literature data (for a
total of 28 RR Lyraes), cluster
metallicities were taken at face value from the literature, even if a zero
point was admittedly noted while using data from different samples. We
have many clusters in
common with the study of Clementini et al. (1995) and have then derived
again the
[Fe/H] vs ![]() relation. Figure 6 (click here) shows the result of our
re-analysis.
relation. Figure 6 (click here) shows the result of our
re-analysis.
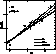
Figure 6: Calibration of the ![]() index with our new analysis and
with the data of field RR Lyrae variables from
Clementini et al. (1995)
index with our new analysis and
with the data of field RR Lyrae variables from
Clementini et al. (1995)
We obtained ![]() values for 15 of our calibrating clusters from the
metallicities of Costar & Smith (1988), inverting the Butler's (1975) relation
they used. Our values are not completely identical to those used by Clementini
et al. (1995); the main differences are that a) we excluded 47 Tuc, since its
value for
values for 15 of our calibrating clusters from the
metallicities of Costar & Smith (1988), inverting the Butler's (1975) relation
they used. Our values are not completely identical to those used by Clementini
et al. (1995); the main differences are that a) we excluded 47 Tuc, since its
value for ![]() is based on a single star, possibly not member of the
cluster (Tucholke 1992) and b) for NGC 288 we assumed a value of
is based on a single star, possibly not member of the
cluster (Tucholke 1992) and b) for NGC 288 we assumed a value of ![]() ,
since the mean value 7.2 cited by Costar & Smith was obtained including
spectra taken at phases near maximum light.
,
since the mean value 7.2 cited by Costar & Smith was obtained including
spectra taken at phases near maximum light.
Regression lines were then obtained by least-squares fits (we averaged values obtained exchanging the independent and dependent variables):
Also shown in Fig. 6 (click here) is the calibration obtained by Clementini et
al. (1995), using only 28 field variables (their equation 6):
[Fe/H]=-0.204(![]() 0.012)
0.012)![]() (
(![]() 0.036),
0.036), ![]() =0.190.
=0.190.
The first striking evidence both from Fig. 6 (click here) and the above
equations is that the sequence of the globular cluster points seems to be much
better defined, with a smaller scatter than the distribution of field RR
Lyraes. The scatter in Eq. (6) of Clementini et al.
is 0.19 dex, to be compared with the value of
0.13 dex obtained using only the new values for the clusters. We stress the
fact that both the solar Fe abundance and the source for the oscillator
strengths are in common between the present analysis and that of Clementini et
al. (1995); moreover, the procedure followed in the abundance analysis is
virtually the same. This may be evidence in favour of a larger intrinsic scatter
in field than in cluster variables, or it may just reflect a smaller
error in the values of ![]() for cluster RR Lyraes. However the last
explanation seems a little unpalatable, since determinations of
for cluster RR Lyraes. However the last
explanation seems a little unpalatable, since determinations of ![]() \
values are usually more accurate for nearby field stars.
\
values are usually more accurate for nearby field stars.
The second feature shown in Fig. 6 (click here) is a rather clear separation between the
relations for cluster and field RR Lyraes in the low metallicity region; this is
the likely explanation for the increase in the scatter when the calibration
[Fe/H]-![]() is made using both cluster and field variables.
The same behaviour was evident also in Fig. 14c of Clementini et al. (1995),
but here it is even clearer, given the high degree of homogeneity in
our data. Why this is so, we are not sure, apart from
a suggestion of non-linearity
in the
is made using both cluster and field variables.
The same behaviour was evident also in Fig. 14c of Clementini et al. (1995),
but here it is even clearer, given the high degree of homogeneity in
our data. Why this is so, we are not sure, apart from
a suggestion of non-linearity
in the ![]() -[Fe/H] relation theoretically predicted (Manduca 1981)
and discussed in Clementini et al. (1995).
Apart from this, there seems to be a good
agreement between both scales; if we use our new calibration (Eq. 12) to
derive [Fe/H] ratios, the differences [Fe/H]
-[Fe/H] relation theoretically predicted (Manduca 1981)
and discussed in Clementini et al. (1995).
Apart from this, there seems to be a good
agreement between both scales; if we use our new calibration (Eq. 12) to
derive [Fe/H] ratios, the differences [Fe/H]![]() - [Fe/H]
- [Fe/H]![]() are on average
are on average ![]() (
(![]() =0.10, for 16 clusters).
=0.10, for 16 clusters).
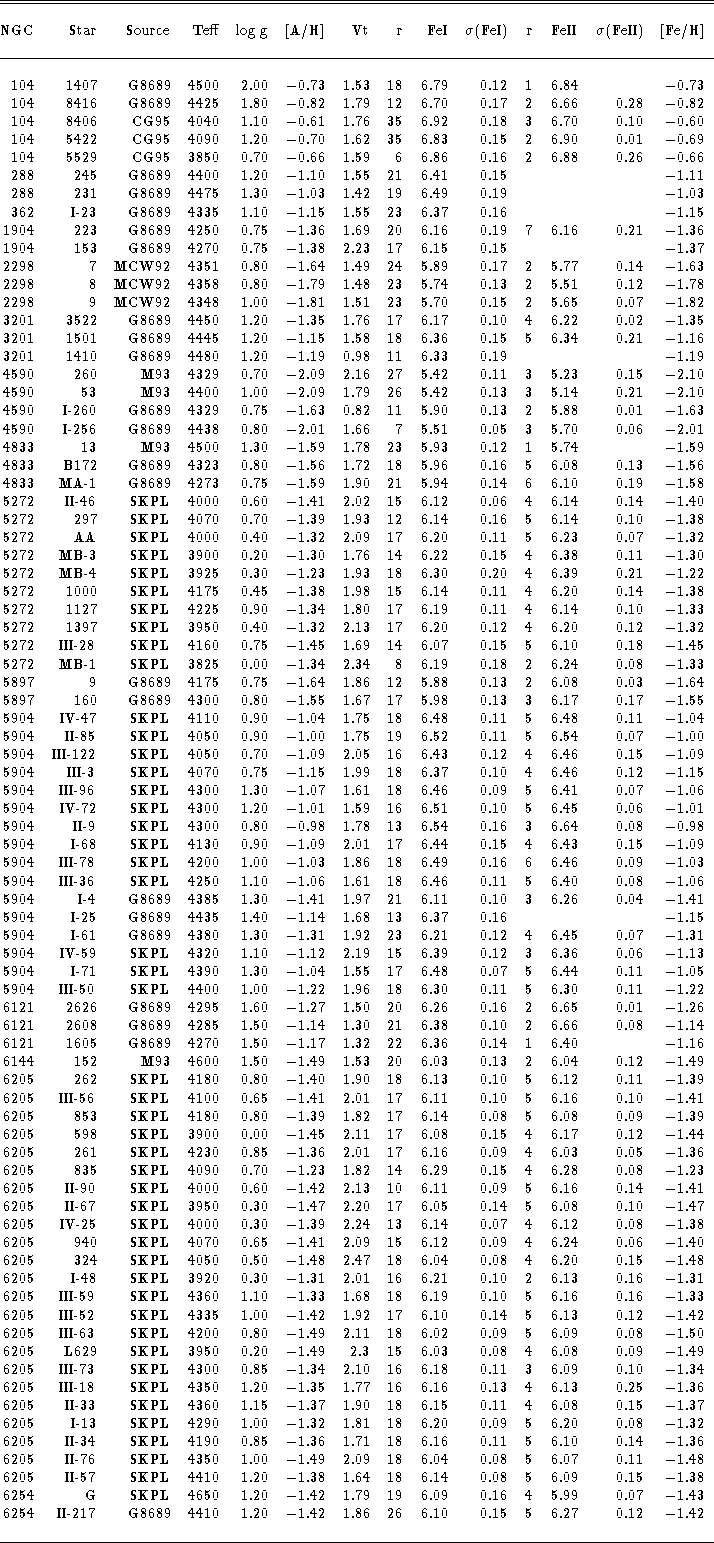
Table 9: Adopted atmospheric parameters and results of abundance analysis
for globular cluster giants