We think that the effort to get more reliable and accurate metallicities is truly worthwhile: a new, homogeneous scale of [Fe/H] for globular clusters is really needed, since up to now the numerous but still heterogeneous estimates from HDS have been systematically ignored in many problems of stellar evolution.
Figure 7: Observed distributions of variables in M 3 (filled squares) and
M 15 (open squares) in the 
plane (see text)
As an illustrative example
we will explore the effects of our new [Fe/H] values on the long-standing
problem of the Oosterhoff (1944) effect among globular clusters, which
belong to 2 groups on the basis of the mean period of their type ab RR Lyraes;
this division reflects a separation in metallicity of the clusters (Arp 1955).
The statement of this problem, its history and references are fully addressed
in a recent paper by Sandage (1993a). Briefly, the concept is to use
the pulsation equation for RR Lyrae stars (
),
where P is the fundamental period of the pulsation, L the luminosity and M the mass of the
star) to derive a calibration of the absolute luminosity of RR Lyraes in terms
of the metal content, [Fe/H], in turn a cornerstone to ultimately get
the ages of globular clusters. This is possible if the
variations of the parameters involved (
)
with [Fe/H] are known.
The critical and more debated point is to determine how 
, the
shift existing in the log 
plane between the distribution of
variables in OoI and OoII clusters, varies with the metallicity; the slope, in
particular, is still much controversial. While Sandage (1993a) finds a value
of about 0.12, theoretical models seem to predict a much lower value,
around 0.05 (in the sense of longer periods for metal-poorer clusters).
Our approach is based both on our new metallicities and new 
's
for variables in
M 3 (OoI) and M 15 (OoII), i.e. the template-pair for the Oosterhoff effect.
(a) From the present work we adopt [Fe/H]=-1.34 for M 3 and [Fe/H]=-2.12 for M 15. These values compare well to those derived by Sneden et al. (1991) and Kraft et al. (1992, [Fe/H]=-1.48 and -2.30 for M 3 and M 15 respectively), allowing for their use of the old Bell et al. (1976) model atmospheres and of a different set of gf.
If one compares these new values with the classical ZW ones (-1.66 for M 3 and
-2.15 for M 15) ,
it it immediately evident that
whatever the period shift between M 3 and M 15 may be,
it has to be ``diluted''
on a larger range of metallicity than before. This in turn affects the
slope of the relationship 
.
b) We adopt here the new temperature scale derived by Gratton et al. (1996).
Briefly, they first derived empirical
colour-
relations for population I stars, based on
's from the Infrared Flux Method (IRFM, Blackwell & Lynas Gray 1994;
Bell & Gustafsson 1989)
and interferometric diameters (Di Benedetto & Rabbia 1987); stars of
luminosity class III and V were considered separately.
's for stars of different 
and [Fe/H] are then obtained
applying systematic corrections to the theoretical K92 
's,
to tie them to the empirical calibrations and to the K92 colours, in
order to take into account the real metallicities (different from
solar). The effect of gravity was taken into account by interpolating
between typical values for dwarfs and giants.
The underlying assumption is that K92 models (the same consistently used in
the abundance analysis) are well able to
reproduce the run of colours with the overall metal content [A/H], but have to
be corrected in function of the surface gravity
(a constant mean value of log g=2.75 was assumed for all variables).
The adopted scale is very similar to the one defined by Clementini et al. (1995)
to study field RR Lyrae stars; they also showed that as far as colours (and
abundances) are concerned, K92 models are well suited to reproduce the
atmospheres of RR Lyrae variables.
The photometry for the variables of M 15 is taken from the high quality work
of Bingham et al. (1984). For M 3, we used colours
from Sandage (1990).
The choice of the mean colour which better represents
the one the variable should have were it not pulsating is not simple (see
e.g., Fernley 1994). However, for sake of
comparison with Sandage's
previous works on M 3, in the present study we use 
,
the corrected colours taken
from the quoted sources; they also include an empirical
correction 
(A)
depending on the light-curve amplitude (Sandage 1990).
We adopt E(B-V)=0.00 for M 3, while for M 15 we assume 0.10 (Zinn 1980).
Figure 7 (click here) shows the observed distributions of variables in M 3
and M 15 in the
classical 
plane (
is the reduced
and fundamentalized period; for c-type RR Lyraes the period is fundamentalized
by adding 0.127 to log P). The lines are best-fits drawn by eye
through the data, since the computed least squares linear regression result
in non-parallel lines, due to the scatter among the data, especially in
those of M 3. This method is good enough in this case, since we are only
interested in presenting and emphasizing another source of uncertainty
affecting this method.
In panel (a) T
's are derived from the old Kurucz (1979) model
atmospheres, following the (unpublished) calibration of Buser, and with
E(B-V)=0.00 and 0.10 for M 3 and M 15 respectively.
Metallicities are on
the Zinn and West's scale: this panel should then reproduce
closely enough Sandage's results for the Oosterhoff effect in the pair
M 3-M 15. In panel (b) we used the new metallicities from the present work
and 
's derived from K92 models.
In order to evaluate the period shift between the two distributions, we
followed the prescriptions of Sandage (1993b), reading the values of 
not at constant 
, but at lower temperatures for lower
metallicities, following his Eq. (5).
Our measurements then give the period shift 
(in the sense
M 15-M 3) = -0.103 and -0.076 for case (a) and (b), respectively.
We note that only the first slope is similar to the one
derived by Sandage (1993a: 
).
Simply using the new metallicities
and effective temperatures, although derived from the same photometric data,
significatively decreases the size of the effect.
Taking at face value these figures, and using the parameters temperature
and mass (along with their variations with metallicity as given by Sandage
1993b) in the pulsation equation of
van Albada & Baker (1973), we obtain
for the slope of the relationship 
vs [Fe/H] the values
0.300 and 0.221 for case (a) and (b) respectively.
As one can see, case (b) is very similar to that derived from the
Baade-Wesselink analyses (0.25, as quoted for instance in Sandage 1993b), whose
results were considered up to now in serious disagreement with the calibration
from the Oosterhoff effect.
This straightforward exercise points out that simply using new, modern, and self-consistent temperatures and metallicities, the size of the Oosterhoff effect in the template pair M 3-M 15 is somewhat reduced, being more consistent with theoretical models of Zero Age Horizontal Branch (see Sandage 1993b for references). We then conclude that our effort in obtaining these new, improved values for metallicities can pay off; we will proceed to a new calibration of photometric / low resolution indices, including all known globular clusters, as soon as a homogeneous dataset will be available.
Acknowledgements
We wish to thank Chris Sneden for useful discussion and encouragement. E.C. warmly thanks Carla Cacciari for providing tables with the parameters of variables in M 3 and M 15 from Kurucz's (1979) models and for many useful suggestions and discussions on the Oosterhoff effect. E.C. acknowledges financial support from the Consiglio Nazionale delle Ricerche.
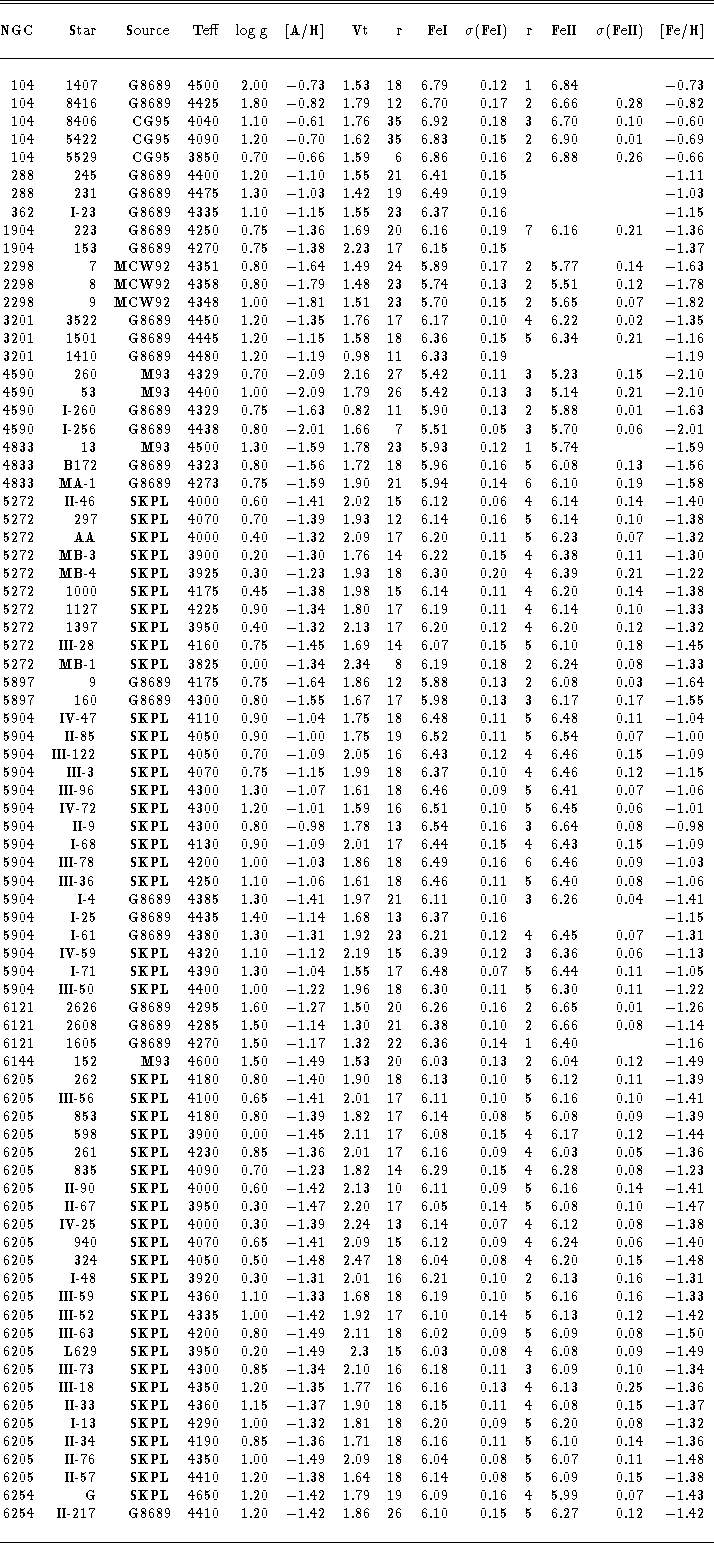
Table 10: Adopted atmospheric parameters and results of abundance analysis
for globular cluster giants
