

Up: A meteorological and photometric
Subsections
The meteorological measurements were recorded from 1990 December to 1993
March. A breakdown of the observing station occurred during the months of
1991 September and 1992 November. The automatic station consists of a data
acquisition unit provided with several analogue channels connected to
meteorological sensors. The parameters measured were wind speed and
direction, relative humidity, air temperature and rainfall. All parameters
were averaged and, together with extreme values, recorded every hour.
Table 3:
Daytime wind statistics (4650 hr). Percentage of time per sector
at Oukaimeden
| |
N |
NNE |
NE |
ENE |
E |
ESE |
SE |
SSE |
S |
SSW |
SW |
WSW |
W |
WNW |
NW |
NNW |
all |
| A |
0 |
0 |
0.1 |
0.2 |
1.3 |
2.2 |
4 |
3.8 |
4.2 |
6.4 |
8.8 |
9.8 |
11.7 |
12.4 |
11.8 |
3.1 |
79.8 |
| B |
0 |
0 |
0 |
0.1 |
0.9 |
2.2 |
1.6 |
1.4 |
1.6 |
1.4 |
1.6 |
1 |
0.7 |
0.8 |
0.8 |
0.4 |
14.5 |
| C |
0 |
0 |
0 |
0 |
0 |
1.1 |
0.9 |
2.4 |
0.9 |
0.4 |
0 |
0 |
0 |
0 |
0 |
0 |
5.7 |
| |
0 |
0 |
0.1 |
0.3 |
2.2 |
5.5 |
6.5 |
7.6 |
6.7 |
8.2 |
10.4 |
10.8 |
12.4 |
13.2 |
12.6 |
3.5 |
100 |
The statistical results of the temperature are presented in Figs. 2-4.
In Fig. 2, we display monthly all-day mean, minimum and
maximum values of the temperature (solid lines). Daytime and night-time mean
temperatures are plotted (dotted and dot-dashed lines, respectively). From our data,
we can see a seasonal variation:
the cold months are October to March and the hot months are
April to September. The daily mean temperature is
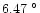 C
(
C
(
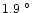 C in winter,
C in winter,
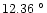 C in summer). The absolute
minimum recorded during the night in 1992 March is
C in summer). The absolute
minimum recorded during the night in 1992 March is
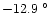 C
and the absolute maximum recorded during the day in 1991 August is
C
and the absolute maximum recorded during the day in 1991 August is
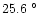 C.
C.
The daytime and night-time mean temperatures are
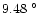 C and
C and
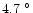 C, respectively. The daytime minimum is
C, respectively. The daytime minimum is
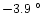 C recorded in 1991 March and the night-time maximum is
C recorded in 1991 March and the night-time maximum is
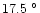 C recorded in 1992 August.
C recorded in 1992 August.
The daily variation of the temperature at Oukaimeden is presented
in Fig. 3. Note that during the night, the temperature
decreases very slowly, due to thermal cooling.
The statistics in temperature difference for two
consecutive nights are illustrated in Fig. 4. The mean temperature
difference is
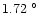 C. The maximum difference is
C. The maximum difference is
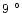 C
recorded in March. The seasonal variation is also negligible and
shows that the stability of the nightly temperature is
considerable at both sites.
C
recorded in March. The seasonal variation is also negligible and
shows that the stability of the nightly temperature is
considerable at both sites.
Following Racine et al. (1991), we have determined the dome ("D'') and
mirror ("M'') contribution to the seeing by using:
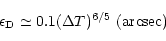 |
(1) |
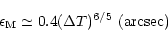 |
(2) |
where 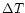 represents the temperature difference between
the dome (or the mirror) and the external atmospheric temperature.
represents the temperature difference between
the dome (or the mirror) and the external atmospheric temperature.
Because most observatories use air conditioning, the difference in temperature
between two consecutive nights might determine the magnitude of the dome and
telescope mirror seeing. Let us define this difference 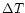 :
:
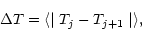 |
(3) |
where j is a given night.
Then 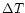 is used in Eqs. (1) and (2).
In Table 1, we present the effect of such temperature difference
on dome and mirror seeing. The seeing variation is mainly produced
by mirror seeing.
is used in Eqs. (1) and (2).
In Table 1, we present the effect of such temperature difference
on dome and mirror seeing. The seeing variation is mainly produced
by mirror seeing.
In Fig. 5, we present the monthly
variation of the daytime, night-time and all-day relative humidity.
Here we also note a seasonal effect. The all-day mean humidity is 45%.
The daytime and night-time mean humidities are 46% and 42%,
respectively. The humid months span from February to June, whereas the driest ones
are from July to January except October and December.
The cumulative frequency of relative humidity is shown in Fig. 6. The
probability of high humidity is weak and given a 90% humidity threshold,
only 8% of the observing time would be lost due to this cause.
The daily variation of relative humidity is shown in Fig. 7. It increases
during the day with a peak at sunset and then drops rapidly at the
beginning of the night. In our experience, this trend is supported by
solar observation which shows us that atmospheric transparency is excellent
in the morning yet decreases during the afternoon (Benkhaldoun 1993). Low
humidity during the night also gives us favourable astronomical conditions.
Wind statistics are presented in Tables 2 and 3 and Figs. 8-11. The
daytime and night-time wind readings are a compilation of a total of 9191
hours (Figs. 8 and 9). The highest wind speed frequency occurs within the
A interval for both daytime (79.8%) and night-time (64.5%). At night
this wind velocity interval peaks in the SE (21.8%) and SW (10.8%),
whereas during the day we see a change in the wind pattern. The wind
prevails from WNW direction (13.2%). Within the B interval, the
frequency distribution peaks at the night-time in the SE (7.1%) and
during the daytime in the ESE (2.2%).
The monthly variation of wind velocity is illustrated in Fig. 10. The
data analysis shows a weak seasonal effect. The mean velocity is 2.63 m s-1.
In all of our data, 60% of time, wind is included between 1 to 3 m s-1
and during 89% it is lower than 5 m s-1 (Fig. 11).
Although the velocity is low enough, we found that the wind can reach a
significant amplitude of 50 m s-1.
We checked that a more than 25 m s-1 wind occurs within 5% of daily maxima and that
a 50 m s-1 maximum occurs in 17 cases out of the 652 daily maxima recorded.
We have also
analysed the wind velocity in terms of telescope management. Assuming a
15 m s-1 threshold (beyond which the telescope would cease operation) we
lose only 0.2% of our research time, particularly in the winter.
![\begin{figure}
{\includegraphics[width=8.8cm]{ds1856f20.eps} }
\end{figure}](/articles/aas/full/2000/20/ds1856/Timg34.gif) |
Figure 12:
Monthly total precipitation at Oukaimeden from
November 1990 to March 1993 |
![\begin{figure}
{\includegraphics[width=8.8cm]{ds1856f21.eps} }
\end{figure}](/articles/aas/full/2000/20/ds1856/Timg35.gif) |
Figure 13:
Monthly variation of atmospheric pressure at ORM |
![\begin{figure}
{\includegraphics[width=8.8cm]{ds1856f22.eps} }
\end{figure}](/articles/aas/full/2000/20/ds1856/Timg36.gif) |
Figure 14:
Monthly variation of photometric nights at ORM |
The analysis of precipitation data allows us to establish that the annual
mean at Oukaimeden is about 362.5 mm. As shown in Fig. 12, the first
three months of 1991 were more rainy than the first quarter of 1992. We
found little seasonal change since precipitation varied drastically from
year to year; nevertheless, June to November is the driest period.
The first results of daytime photometry at Oukaimeden site were
published by Benkhaldoun et al. (1993). He found an extinction
coefficient of 0.13 mag/air mass and a fraction of clear weather
of 65%. Measurements of solar luminosity were performed
simultaneously at three wavelengths (550, 589, 700 nm). The
instrument used for those observations is a simple Flux
Integration Photometer (FIP). For the description
of this instrument and data reduction see Benkhaldoun (1993). The
photometric quality of Oukaimeden is evaluated by using
the least squares method applied to the data set. The atmospheric
extinction coefficient is determined from the Bouguer straight
line technique (Benkhaldoun 1994).
Using GONG data Hill et al. (1994a,b) found a slightly different
result for the clear weather fraction statistics (50%) and the
extinction coefficient equals to 0.12 mag/air mass.
If the values found for the extinction are analogous (0.13 and 0.12),
it is not the case for the clear time fraction (65% and 50%). This difference
is partly systematic explaining by the way of conception of the two instruments,
the FIP with his system of diffuser measuring the totality of the light in source
of sky whereas the GONG instrument measures the incidental direct radiance.
Indeed, during another observation period,
(January 1992 - November 1992),
we performed a cross calibration between
the two instruments, which gave us a fraction of
clear weather at Oukaimeden of
57% for FIP and 53% for GONG (Siher et al. 1996).
Another reason that lowers the fraction of clear weather
issued by the GONG instrument lies in the frequency of the breakdowns. The
most significant cause of breakdowns is due to power failures that occur
during storms.The GONG
instrument does not work for several days, when we generally experience
clear and favorable weather. Meanwhile, during this time, the FIP
instrument is working normally.
A battery gives an autonomy for a limited amount of time to GONG experiment, but it
requires an human intervention to start again, after this time out. On the contrary,
the FIP experiment automatically switches on after a breakdown.
This affects the overall statistics as it has been shown by Benkhaldoun (1994). He
demonstrates that, over three different periods (at the begining, in the middle and
at the end of the measurement campaign), a decrease of 20% of breakdown periods
results in a 10% increase of clear time fraction.
The 1997 IRIS results (Benkhaldoun et al. 1998)
are in agreement with the first photometric data published by Benkhaldoun et al. (1993).
Table 4:
Night-time wind statistics. Percentage of time in sector (in%) at
ORM
| |
N |
NNE |
NE |
ENE |
E |
ESE |
SE |
SSE |
S |
SSW |
SW |
WSW |
W |
WNW |
NW |
NNW |
all |
| A |
4.3 |
3.7 |
4.3 |
3.3 |
2.3 |
2.3 |
4.4 |
2.9 |
2.1 |
1.9 |
1.6 |
1.3 |
1.3 |
1.7 |
1.9 |
2.2 |
41.5 |
| B |
4.9 |
2.2 |
3.8 |
3.7 |
2 |
1.3 |
2.1 |
2.2 |
2.5 |
2.8 |
3.4 |
2.5 |
1.4 |
2 |
3.4 |
5.8 |
46 |
| C |
1.3 |
0.2 |
0.3 |
0.6 |
0.4 |
0.2 |
0.3 |
0.3 |
0.8 |
1.4 |
2.1 |
0.9 |
0.3 |
0.3 |
0.7 |
2.4 |
12.5 |
| |
10.5 |
6.1 |
8.4 |
7.6 |
4.7 |
3.8 |
6.8 |
5.4 |
5.4 |
6.1 |
7.1 |
4.7 |
3 |
4 |
6 |
10.4 |
100 |
Table 5:
Daytime wind statistics. Percentage of time in sector (in%) at ORM
| |
N |
NNE |
NE |
ENE |
E |
ESE |
SE |
SSE |
S |
SSW |
SW |
WSW |
W |
WNW |
NW |
NNW |
all |
| A |
6.7 |
4.6 |
3.8 |
2.5 |
1.4 |
1.3 |
2.6 |
4.5 |
3.7 |
2.3 |
2.1 |
2.2 |
1.9 |
2 |
2.6 |
3.6 |
47.8 |
| B |
4.2 |
1.6 |
2.1 |
2.2 |
1.3 |
1 |
2 |
3.3 |
2.5 |
2.1 |
3.3 |
4.1 |
2.7 |
2.2 |
3.3 |
4.3 |
42.2 |
| C |
0.8 |
0.1 |
0.3 |
0.3 |
0.2 |
0.2 |
0.3 |
0.3 |
0.6 |
0.9 |
1.7 |
1.5 |
0.6 |
0.3 |
0.6 |
1.3 |
10 |
| |
11.7 |
6.3 |
6.2 |
5 |
2.9 |
2.5 |
4.9 |
8.1 |
6.8 |
5.3 |
7.1 |
7.8 |
5.2 |
4.5 |
6.5 |
9.2 |
100 |


Up: A meteorological and photometric
Copyright The European Southern Observatory (ESO)
![\begin{figure}
{\includegraphics[width=8.8cm]{ds1856f21.eps} }
\end{figure}](/articles/aas/full/2000/20/ds1856/Timg35.gif)
![\begin{figure}
{\includegraphics[width=8.8cm]{ds1856f22.eps} }
\end{figure}](/articles/aas/full/2000/20/ds1856/Timg36.gif)