

Up: Achromatic interfero coronagraphy
Subsections
6 Limitations regarding detection capability
In order to improve the performance of AIC one wants to know the relative weights
of
the various limitations. Far from the star the main limitation comes from the
camera
noise but close to the star it is the residual energy from the star which decreases
the detectivity. This latter limitation is the most annoying since it tends to
cancel
a specific advantage of AIC (close sensing capability) and since AO correction is
particularly efficient close to AIC axis (Paper I). This residual energy comes from
the corruption of the wavefront by optical aberrations. These aberrations can be
divided into the optical aberrations before the AIC (residual turbulence through
the
AO, fixed aberrations in the wavefront sensor unit or in the optical set-up after
the
AO beamsplitter), the optical aberrations inside AIC, and the OPD variations (which
could be also included into the aberrations inside AIC).
6.2 OPD variations
From laboratory tests, we know that the contributions of the various aberrations
inside AIC amount to less than 0.5% of the integrated energy without AIC. Besides,
we have already said that OPD residual fluctuations were exceedingly large, as a
result of the unexpected vibrations of the building structure and of numerous
acoustic perturbations (rms variation about
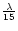 in IR).
in IR).
In Appendix A: we show that the main contribution to the residual energy
of
AIC comes from these OPD variations. The mean intensity in the output image plane
takes the form:
with
As explained in Paper I, and as appearing in the formulae, the summation
in the first term applies only on Zernike polynomials with odd radial degree. Since
 for
for  for n>1, the summation in the first term is
null
for small
for n>1, the summation in the first term is
null
for small 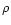 ,
and there is no contribution from the first term on the axis of
AIC.
The observed radial profile of the residual energy coming out of AIC
shows a central peak (see Fig. 5). The second term explains this a
priori unexpected shape, and is much likely to be the major cause yielding the
central peak, eventhough the finite pixel size contribute to this central
peak (see Sect. 5.2). In other words when RT.<d2> is not null the
central pixel is not utterly dark.
Taking this into account we calculate the coefficient RT.<d2> that is a
weighting
factor to apply to the theoretical diffraction pattern without coronagraph.
The coefficient RT.<d2> for our data exhibits a mean value of 2.5% and varies
between 1.5% to 3% from one star to another one. This is consistent with the
variation of
,
and there is no contribution from the first term on the axis of
AIC.
The observed radial profile of the residual energy coming out of AIC
shows a central peak (see Fig. 5). The second term explains this a
priori unexpected shape, and is much likely to be the major cause yielding the
central peak, eventhough the finite pixel size contribute to this central
peak (see Sect. 5.2). In other words when RT.<d2> is not null the
central pixel is not utterly dark.
Taking this into account we calculate the coefficient RT.<d2> that is a
weighting
factor to apply to the theoretical diffraction pattern without coronagraph.
The coefficient RT.<d2> for our data exhibits a mean value of 2.5% and varies
between 1.5% to 3% from one star to another one. This is consistent with the
variation of
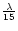 rms in IR observed during the run. One must keep
in
mind that about 0.5% of the integrated energy comes from the AIC aberrations but
for
such small aberrations the contribution on the axis is negligible.
rms in IR observed during the run. One must keep
in
mind that about 0.5% of the integrated energy comes from the AIC aberrations but
for
such small aberrations the contribution on the axis is negligible.


Up: Achromatic interfero coronagraphy
Copyright The European Southern Observatory (ESO)
![\begin{displaymath}I(\vec{\rho}) \approx RT \left[<\vert 2\sum_{\mathrm{odd},i=J...
...rho})}\vert^2>+<d^2\vert\hat{Z}_{1}(\vec{\rho})\vert^2>\right]
\end{displaymath}](/articles/aas/full/2000/14/ds9360/img40.gif)
![\begin{displaymath}I(\vec{\rho}) \approx RT \left[<\vert 2\sum_{\mathrm{odd},i=J...
...rho})}\vert^2>+<d^2\vert\hat{Z}_{1}(\vec{\rho})\vert^2>\right]
\end{displaymath}](/articles/aas/full/2000/14/ds9360/img40.gif)