

Up: Achromatic interfero coronagraphy
Appendix A: Contribution of the aberrations to the residual energy on the axis of the
AIC
We calculate here the mean intensity behind AIC with an OPD error:
We approximate
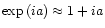 because the fluctuations of the
turbulent phase are small because the first aberrations are corrected by the AO.
The
fluctuations of the OPD are also small (about
because the fluctuations of the
turbulent phase are small because the first aberrations are corrected by the AO.
The
fluctuations of the OPD are also small (about
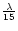 in IR).
in IR).
We develop the phase errors in Zernike polynomials
(Noll 1976, Paper I). The
even Zernike polynomials are removed because of the rotation of the pupil in one
arm
and the sum is only done on odd radial polynomials.
Remembering that
 and calling
and calling
![$\mathrm{TF}[Z_i(\vec{r})]_{\vec{\rho}}=\hat{Z_i}(\vec{\rho})$](/articles/aas/full/2000/14/ds9360/img56.gif)
As

depends on i-k the term
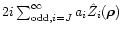 is real while the term
is real while the term
 is
imaginary.
is
imaginary.
Then the cross values are null and we obtain:
The first term is the same as the one found in Paper I and gives no light
contribution on the axis of the AIC. The second term is then the term that explains
the residual peak found on the axis of the AIC.
Acknowledgements
We are grateful to the Observatoire de Haute Provence staff and the Office
Nationale
d'Étude et de Recherche Aérospatiale staff.
Part of this work has been performed using the computing facilities
provided by the program "Simulations Interactives et Visualisation en
Astronomie et Mécanique (SIVAM)''.


Up: Achromatic interfero coronagraphy
Copyright The European Southern Observatory (ESO)
![\begin{eqnarray*}I(\vec{\rho})
&=&
RT<\vert{\rm TF}
[P(
{\bf r}
)
\exp
\left(
i...
...{\bf r})
\right)
\exp
\left(
id
\right)
]_{\vec{\rho}}\vert^2 >.
\end{eqnarray*}](/articles/aas/full/2000/14/ds9360/img51.gif)
![\begin{eqnarray*}I(\vec{\rho})
&=&
RT<\vert{\rm TF}
[P(
{\bf r}
)
\exp
\left(
i...
...{\bf r})
\right)
\exp
\left(
id
\right)
]_{\vec{\rho}}\vert^2 >.
\end{eqnarray*}](/articles/aas/full/2000/14/ds9360/img51.gif)
![\begin{displaymath}I(\vec{\rho})\approx RT<\vert\mathrm{TF}[2i\sum_{{\rm odd},i=...
...fty}{a_{i}
Z_{i}(\vec{r})}-idP(\vec{r})]_{\vec{\rho}}\vert^2>.
\end{displaymath}](/articles/aas/full/2000/14/ds9360/img54.gif)
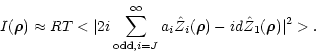

![\begin{displaymath}I(\vec{\rho}) \approx RT \left[<\vert 2\sum_{\mathrm{odd},i=J...
...ho})}\vert^2>+<d^2\vert\hat{Z}_{1}(\vec{\rho})\vert^2>\right].
\end{displaymath}](/articles/aas/full/2000/14/ds9360/img61.gif)