

Up: AGAPEROS: Searching for variable Method
Subsections
4 Magnitude estimation
![\begin{figure}
\includegraphics[width=9cm]{lflmc.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg52.gif) |
Figure 4:
Luminosity functions in blue (full line) and in red (dashed
line) at the epoch JD = 2448678.3. The upper histograms a)
correspond to the magnitudes estimated for all the stars with
DAOPHOT. The lower histograms b) correspond to the magnitudes
estimated as described in Sect. 4.1 for the selected
variable stars |
Whereas the pixel method of analysis is able to detect variable stars
beyond the crowding limit, it does not measure photometry - total
flux - of these objects, that can be blended or even unresolved on
part of the light curves. Obtaining their photometry would give a
first indication of the type of the variable stars. Hence in this
section, we associate a magnitude and colour to each flux measurement.
4.1 Pseudo-aperture photometry
As discussed in Paper II, the flux of the super-pixel is composed of
the fraction of the flux of the star plus the local background
(from sky and undetected stars). For our sample of variable stars, we
can presume that there is a star within the corresponding super-pixel
and that its flux significantly contributes to this super-pixel, at
least at the maximum of the variation. Because of the crowding
conditions, standard background estimates (circular annulus for
example, see Stetson 1987) fail and cannot be
used in an automatic way. Hence, we choose to perform a
pseudo-aperture photometry as follows. For an image taken in the
middle of the period of observation (JD 2448678.3) and with an average
seeing, we use the PSF fitting procedure of DAOPHOT (Stetson
1987) to measure the fluxes of the resolved
stars, and the background below them. This thus gives a local estimate
of the background that is the less affected by the crowding of the
field. Then for each selected super-pixel we look for the detected
star that is closest. The background estimate associated with this
star is supposed to be the same as the one present below the variable
star (and is even identical if the variable stars are resolved on this
reference frame). This background is subtracted from the super-pixel
flux. This flux is then corrected for the seeing fraction and
converted into a magnitude, corresponding to an isolated star.
Whereas this definition of the sky-background is rather robust to the
crowding conditions, the magnitude estimation is not necessary so, as
some additional flux (stellar background) could contribute to the
super-pixel due to neighbours. We thus quantify the blending with the
ratio
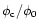 computed as follows: the flux
computed as follows: the flux
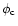 is the
averaged value computed along the light curve of the central pixel of
the super-pixel, and the flux
is the
averaged value computed along the light curve of the central pixel of
the super-pixel, and the flux 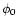 is a similar average of the 8
surrounding pixels within the super-pixel. The behaviour of this
parameter is described in the Appendix.
is a similar average of the 8
surrounding pixels within the super-pixel. The behaviour of this
parameter is described in the Appendix.
Optimised star detection with DAOPHOT allows to detect  stars in blue and
stars in blue and 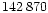 stars in red. The corresponding
luminosity function computed with DAOPHOT for all the stars present on
the studied field, exhibited in Fig. 3a, shows that the
star detection is in first approximation complete down to magnitude 18
in red and 19 in blue. Figure 3b shows that the magnitude
distributions at the same epoch for the selected variable stars peak
at the bright end, whereas the stars are redder than average with
stars in red. The corresponding
luminosity function computed with DAOPHOT for all the stars present on
the studied field, exhibited in Fig. 3a, shows that the
star detection is in first approximation complete down to magnitude 18
in red and 19 in blue. Figure 3b shows that the magnitude
distributions at the same epoch for the selected variable stars peak
at the bright end, whereas the stars are redder than average with
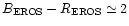 .
Whereas it is difficult to
compute our detection efficiencies as no reliable theoretical
distribution of variable stars is available, it is clear that we do
not detect a population of variable stars unresolved at minimum, even
though we do detect a tail of this distribution with very dim stars in
at least one colour.
.
Whereas it is difficult to
compute our detection efficiencies as no reliable theoretical
distribution of variable stars is available, it is clear that we do
not detect a population of variable stars unresolved at minimum, even
though we do detect a tail of this distribution with very dim stars in
at least one colour.
![\begin{figure}
\bigskip
\includegraphics[width=10cm]{cmd.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg59.gif) |
Figure 5:
CMD at JD = 2448678.3: small dots
correspond to the stars detected with DAOPHOT, symbols to the
631 selected variations. The different symbols correspond to different
ranges of the
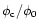 ratio: filled symbols correspond
to stars with a high S/N ratio and not affected by crowding. The
superimposed isochrones (full lines) are adapted from Bertelli et al. (1994)
to the EROS system (Grison et al. 1995) with a
foreground extinction
ratio: filled symbols correspond
to stars with a high S/N ratio and not affected by crowding. The
superimposed isochrones (full lines) are adapted from Bertelli et al. (1994)
to the EROS system (Grison et al. 1995) with a
foreground extinction
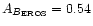 and
and
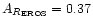 ,
deduced from reddening
E(B-V)=0.15 measured by
Schwering ,
deduced from reddening
E(B-V)=0.15 measured by
Schwering  Israel (1991) with the extinction law from Cardelli et al.
(1989). They correspond to LMC metalicity (Z=0.008),
helium abundance (Y=0.25) with ages of
Israel (1991) with the extinction law from Cardelli et al.
(1989). They correspond to LMC metalicity (Z=0.008),
helium abundance (Y=0.25) with ages of  (age) = 7.4, 8.4 and
9.4. The dashed lines show the uncertainties introduced on each
isochrone by the photometric transformation (age) = 7.4, 8.4 and
9.4. The dashed lines show the uncertainties introduced on each
isochrone by the photometric transformation |
4.2 Colour-magnitude diagram
Figure 4 displays the position of the 631 variable
stars in the CMD. This CMD has been obtained with the resolved stars
detected with DAOPHOT in both colours. The conversion of the EROS
magnitudes into a standard system has been studied by Grison et
al. (1995), but introduces significant systematic
errors especially for stars with
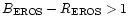 .
We hence
choose to work in the EROS system. The crowding limit prevents the
detection of stars with
.
We hence
choose to work in the EROS system. The crowding limit prevents the
detection of stars with
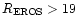 .
The main sequence and red clump
are clearly identified. Very little variations of the CMD are observed
from one chip to another suggesting a uniform stellar population
across this field. The vast majority of the detected variable stars
lies in the red part. A visual inspection of the corresponding light
curves shows that they are compatible with LT
.
The main sequence and red clump
are clearly identified. Very little variations of the CMD are observed
from one chip to another suggesting a uniform stellar population
across this field. The vast majority of the detected variable stars
lies in the red part. A visual inspection of the corresponding light
curves shows that they are compatible with LT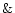 LPV. This
catalogue offers the perspective to systematically study the later
stages of stellar evolution within the LMC Bar. However, the
isochrones superimposed in Fig. 4 illustrate the
difficulty to classify variable stars with the sole CMD, as it is
impossible to disentangle their age and mass for a given
metalicity. The photometric system made it also inappropriate for
further interpretation with this sole data. Due to their complexity
and the difficulties to model them, the LT
LPV. This
catalogue offers the perspective to systematically study the later
stages of stellar evolution within the LMC Bar. However, the
isochrones superimposed in Fig. 4 illustrate the
difficulty to classify variable stars with the sole CMD, as it is
impossible to disentangle their age and mass for a given
metalicity. The photometric system made it also inappropriate for
further interpretation with this sole data. Due to their complexity
and the difficulties to model them, the LT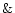 LPV are better
characterised in the IR, as addressed in a subsequent paper. Some
"bluer'' objects have also been detected and they will be classify
when we study their periodicity.
LPV are better
characterised in the IR, as addressed in a subsequent paper. Some
"bluer'' objects have also been detected and they will be classify
when we study their periodicity.
As shown in Fig. 4, variable stars not
significantly affected by crowding (
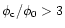 )
lie in areas of
the colour-magnitude diagram corresponding to stars expected
variable. Those affected by blending and crowding will have to be
treated with caution. In the CMD areas where the larger number of
LT
)
lie in areas of
the colour-magnitude diagram corresponding to stars expected
variable. Those affected by blending and crowding will have to be
treated with caution. In the CMD areas where the larger number of
LT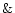 LPV have been detected, in the magnitude (
LPV have been detected, in the magnitude (
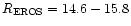 )
and colour (
)
and colour (
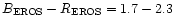 )
ranges, about 17% of the
stars exhibit a variation detected with our analysis.
)
ranges, about 17% of the
stars exhibit a variation detected with our analysis.
It is also clear that the vast majority of the detected variable stars
are above the crowding limit. The few outliers that can be noticed
correspond to stars unresolved in at least one colour, but their
number does not exceed 5% of the total. In terms of
microlensing, this means that events due to unresolved stars in the
LMC will not be significantly contaminated by the bulk of variable
stars. In further galaxies, like M31, variable stars will be a more
troublesome affair, and will have to be carefully studied (e.g. Crotts
& Tomaney 1996). However, high amplification
microlensing events are far less likely to be mimicked by an intrinsic
variation (Ansari et al. 1999), and will allow to
probe possible biases introduced by variable stars.


Up: AGAPEROS: Searching for variable Method
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\includegraphics[width=9cm]{lflmc.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg52.gif)
![\begin{figure}
\bigskip
\includegraphics[width=10cm]{cmd.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg59.gif)