

Up: AGAPEROS: Searching for variable Method
Subsections
3 Selection of genuine variable stars
![\begin{figure}
\includegraphics[width=10cm]{effilpv.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg37.gif) |
Figure 1:
Effect of the selection procedure on the Max(LB,LR)distribution. Panel a) illustrates the effect of the steps (1)
and (2) of the selection procedure indicated in Table
1. The hatched area corresponds to the pixels
kept at step (1). The dashed and dotted histograms each show how this
distribution is affected if this threshold is changed as indicated in
Table 1. The thick line displays the effect of
step (2). The dot-dashed lines correspond to the
weakening/strengthening of this cut. Panel b) illustrates the
effects of steps (4) and (5). The large amplitude histogram shows the
distribution after step (3), the thick-line histogram shows the result
of step (4), and the hatched area corresponds to pixels kept at the
end of step (5). The dashed histograms show the sensitivity of this
last threshold |
We apply an automatic selection of genuine luminosity variations to
the 91-92 dataset. Firstly, we introduce the definition of a
variation. Secondly, we adjust the thresholds in order to keep genuine
variations but reject most artifacts due to noise. Last, we carefully
inspect selected light curves close to bad pixels.
A baseline flux (
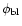 )
is calculated for each super-pixel light
curve by sorting all points in order of increasing flux, with
)
is calculated for each super-pixel light
curve by sorting all points in order of increasing flux, with
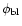 being the 10
being the 10 sorted point.
sorted point.
 is the
error associated with the baseline flux determination. For a sample
taken from a Gaussian distribution with a standard deviation
is the
error associated with the baseline flux determination. For a sample
taken from a Gaussian distribution with a standard deviation 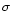 this estimate lies 1.3
this estimate lies 1.3 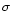 below the mean value of the
distribution.
below the mean value of the
distribution.
Deviations from this baseline are recorded when measurements lie
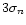 above the baseline:
above the baseline:
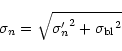 |
(2) |
where
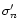 is the error associated with each
super-pixel flux computed in Paper I for night n. These
deviations are quantified in each colour with a likelihood function
(L):
is the error associated with each
super-pixel flux computed in Paper I for night n. These
deviations are quantified in each colour with a likelihood function
(L):
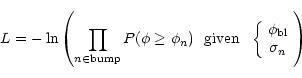 |
(3) |
where 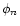 is the super-pixel flux for the measurement n. All
the measurements above
is the super-pixel flux for the measurement n. All
the measurements above
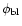 are accounted for.
are accounted for.
With the definition introduced above, we apply the selection
procedure summarised in Table 1.
First of all we excise the pixels, covering 3.4% of the CCD fields,
which exhibit obvious spurious variations (such as bad columns). In
addition, in order to remove automatically artifacts due to bad
pixels, we remove from the light curves the epochs for which there is
at least one pixel which datum is at zero within a 11 11 window
centred on the super-pixel. (1) We require a regularity condition to
remove the noise: the ratio
11 window
centred on the super-pixel. (1) We require a regularity condition to
remove the noise: the ratio
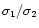 has to be smaller than
0.6 in at least one colour, with:
has to be smaller than
0.6 in at least one colour, with:
![\begin{displaymath}{\sigma_1}^2={\frac{2}{3(N-2)} {\sum_{n=2}^{N-1}}\left[
\frac{\phi_{n+1} - \phi_{n-1}}{2} - \phi_n \right]^2}
\end{displaymath}](/articles/aas/full/2000/13/ds9463/img48.gif) |
(4) |
![\begin{displaymath}{\sigma_2}^2={\frac{1}{(N-1)} {\sum_{n=1}^{N}}\left[
\phi_{n} - \phi_{\rm mean} \right]^2}
\end{displaymath}](/articles/aas/full/2000/13/ds9463/img49.gif) |
(5) |
where
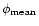 is the mean super-pixel flux and N is the total
number of measurements on each light curve. (2) We then select the
light curves which vary such that L>400 in at least one colour. As
there are as many super-pixels as pixels, a genuine variable is
expected to affect all the super-pixels within the seeing spot. (3) We
search for clusters of super-pixels (using a Friend of Friends
algorithm), and keep the central pixel of the clusters if (4) the
previous requirements are also satisfied for these pixels and, if (5)
the number
is the mean super-pixel flux and N is the total
number of measurements on each light curve. (2) We then select the
light curves which vary such that L>400 in at least one colour. As
there are as many super-pixels as pixels, a genuine variable is
expected to affect all the super-pixels within the seeing spot. (3) We
search for clusters of super-pixels (using a Friend of Friends
algorithm), and keep the central pixel of the clusters if (4) the
previous requirements are also satisfied for these pixels and, if (5)
the number
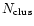 of super-pixels that compose each cluster is
larger than 6. These requirements eliminate most artifacts due to
bright stars
of super-pixels that compose each cluster is
larger than 6. These requirements eliminate most artifacts due to
bright stars![[*]](/icons/foot_motif.gif) and CCD defects
that do not exhibit a clear spatial PSF-like pattern. We finally keep
747 super-pixel light curves. The sensitivity of these thresholds is
illustrated in Fig. 1. Among the 747 selected variations,
two have been counted twice
and CCD defects
that do not exhibit a clear spatial PSF-like pattern. We finally keep
747 super-pixel light curves. The sensitivity of these thresholds is
illustrated in Fig. 1. Among the 747 selected variations,
two have been counted twice![[*]](/icons/foot_motif.gif) , leaving 745 independent light curves.
, leaving 745 independent light curves.
3.3 Artifact removals
![\begin{figure}
\includegraphics[width=9cm]{cleand.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg51.gif) |
Figure 2:
Artifact removals. Panel a) displays the positions of
the 116 rejected light curves on the CCD chips. Panel b) shows a
similar distribution but for those among the 237 light curves close to
CCD defects that have been kept. Each symbol corresponds to a
different chip. Each panel corresponds to the size of the chips
![$x \in [0,400]$](/articles/aas/full/2000/13/ds9463/img1.gif) , ,
![$y \in [0,579]$](/articles/aas/full/2000/13/ds9463/img2.gif)
|
We select 237 light curves for which there is at least one bad pixel
(saturated or set at zero) within a 21 21 window centred on the
selected pixel for at least one epoch and at least one colour. A
careful visual inspection of these light curves shows 121 genuine
variable stars against 116 artifacts, subsequently
removed. Figure 2 shows that the removed light curves
are mainly concentrated close to the edges, whereas the distribution
of the kept light curves (among the 237) is more uniform. We finally
end with a catalogue of 631 variable stars.
21 window centred on the
selected pixel for at least one epoch and at least one colour. A
careful visual inspection of these light curves shows 121 genuine
variable stars against 116 artifacts, subsequently
removed. Figure 2 shows that the removed light curves
are mainly concentrated close to the edges, whereas the distribution
of the kept light curves (among the 237) is more uniform. We finally
end with a catalogue of 631 variable stars.


Up: AGAPEROS: Searching for variable Method
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\includegraphics[width=10cm]{effilpv.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg37.gif)
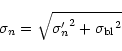
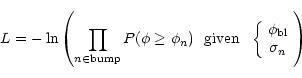
![\begin{displaymath}{\sigma_1}^2={\frac{2}{3(N-2)} {\sum_{n=2}^{N-1}}\left[
\frac{\phi_{n+1} - \phi_{n-1}}{2} - \phi_n \right]^2}
\end{displaymath}](/articles/aas/full/2000/13/ds9463/img48.gif)
![\begin{displaymath}{\sigma_2}^2={\frac{1}{(N-1)} {\sum_{n=1}^{N}}\left[
\phi_{n} - \phi_{\rm mean} \right]^2}
\end{displaymath}](/articles/aas/full/2000/13/ds9463/img49.gif)
![\begin{figure}
\includegraphics[width=9cm]{cleand.eps}\end{figure}](/articles/aas/full/2000/13/ds9463/Timg51.gif)