

Up: Adaptive optics imaging of H
Subsections
We have made a series of tests that tends to strengthen our confidence
in the 59 Cyg's image as a correct PSF for P Cyg. These tests are
negative tests in the sense that if the PSF fails to succeed one, it
should be rejected as a bad PSF.
Let us assume that 59 Cyg is a good unbiased representation of the true PSF h(r).
Differences between the blurred reconstructed image
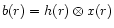 and
the observed data y(r) must then be dominated by statistical noise fluctuations,
with no bias term. In this relation, x(r) is our best reconstructed image, as shown in
Fig. 4, and h(r) the PSF 59 Cyg of Fig. 1 of the body of the paper.
We assume that the noise comes from a photo-detection process, and that y(r) is
a realization of the Poisson process of mean b(r).
and
the observed data y(r) must then be dominated by statistical noise fluctuations,
with no bias term. In this relation, x(r) is our best reconstructed image, as shown in
Fig. 4, and h(r) the PSF 59 Cyg of Fig. 1 of the body of the paper.
We assume that the noise comes from a photo-detection process, and that y(r) is
a realization of the Poisson process of mean b(r).
The first test we have performed is a basic one, not very sensitive to
the exact value of h(r), but that must be verified in any case. Let us
denote y and b the values taken by y(r) and b(r). The total
probability theorem ([Papoulis 1984]) allows us to write the unconditional
probability P(y) of y(r) as the sum of
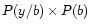 for all bvalues. For the Poisson process, the conditional probability of yassuming b is
for all bvalues. For the Poisson process, the conditional probability of yassuming b is
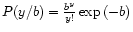 where y is an
integer (the number of photons) and b a continuous value.
where y is an
integer (the number of photons) and b a continuous value.
As a consequence, P(y) is the Poisson-Mandel transform ([Mandel 1959];
[Mehta 1970]) of P(b):
 |
(A1) |
We have verified that our data correctly obeys relation A1. We
have taken for P(b) the histogram of b(r), applied the
above transformation and compared the result
P(y) with the direct histogram of the values of y(r). The
comparison is shown in Fig. A1. The results are consistent with the
data.
The second test we have performed was to check the correctness of the
small departures from circular symmetry of 59 Cyg. We use as the PSF
 an image of 59 Cyg rotated by an angle
an image of 59 Cyg rotated by an angle 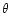 .
Then the deconvolution procedure is carried out as previously
and leads to an image
.
Then the deconvolution procedure is carried out as previously
and leads to an image
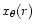 .
The blurred image
.
The blurred image
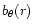 is obtained as the convolution of
is obtained as the convolution of
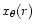 and
and
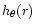 ,
and we finally compute the Euclidean distance between
y(r) and
,
and we finally compute the Euclidean distance between
y(r) and
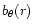 .
The results are shown in Fig. A2
in a polar plot for
.
The results are shown in Fig. A2
in a polar plot for 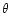 varying from 0 to 2
varying from 0 to 2 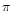 .
The original PSF gives the
best result. If the deviation from circular symmetry was purely
random, the goodness of the deconvolution would not be affected by
this rotation. Secondary minima of the curve appear for apparent
symmetries of the PSF.
.
The original PSF gives the
best result. If the deviation from circular symmetry was purely
random, the goodness of the deconvolution would not be affected by
this rotation. Secondary minima of the curve appear for apparent
symmetries of the PSF.
![\begin{figure}
\includegraphics[width=7cm]{ds9553fA1.eps}\end{figure}](/articles/aas/full/2000/12/ds9553/Timg54.gif) |
Figure A1:
Thick line: Poisson-Mandel transform P(y) of P(b) calculated using
relation A1. Thin line: Histogram of the values of y(r). A good agreement
between the two curves is observed |
![\begin{figure}
\includegraphics[width=7cm]{ds9553fA2.eps}\end{figure}](/articles/aas/full/2000/12/ds9553/Timg55.gif) |
Figure A2:
Thick line: Polar plot of the Euclidean distance between y(r) and
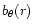 for
for 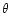 varying between 0 and 2
varying between 0 and 2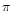 .
Thin
line: Circle with a radius of the minimum of the Euclidean distance
between y(r) and .
Thin
line: Circle with a radius of the minimum of the Euclidean distance
between y(r) and
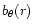 .
The minimum of the Euclidean
distance is obtained for .
The minimum of the Euclidean
distance is obtained for 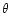 = 0
= 0 |
![\begin{figure}
\includegraphics[width=7cm]{ds9553fA3.eps}\end{figure}](/articles/aas/full/2000/12/ds9553/Timg56.gif) |
Figure A3:
Representation of the sign of the difference
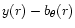 for no
rotation of the PSF (top) and for a rotation of
for no
rotation of the PSF (top) and for a rotation of 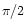 (bottom). This later image is not
a particular case, and is characteristic of what can be obtained when the PSF is rotated
(bottom). This later image is not
a particular case, and is characteristic of what can be obtained when the PSF is rotated |
Representations of the difference between y(r) and
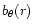 are shown in Fig. A3. For the sake of clarity we have represented the
sign of the difference
are shown in Fig. A3. For the sake of clarity we have represented the
sign of the difference
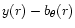 .
For
.
For
 ,
we get a
speckle-like pattern, roughly uniform over the whole image. For other
values of
,
we get a
speckle-like pattern, roughly uniform over the whole image. For other
values of 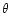 ,
this difference shows large patterns that indicates
regions over which
,
this difference shows large patterns that indicates
regions over which
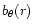 does not correctly match
y(r). These trends clearly show that
does not correctly match
y(r). These trends clearly show that
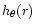 for
for
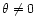 is a biased version of h(r).
is a biased version of h(r).
As a conclusion, 59 Cyg passed the tests and could not be rejected
as a bad PSF.
Acknowledgements
We wish to acknowledge A. Labeyrie for having encouraged the present
work. P Cyg's observations were done using the BOA Adaptive Optics
provided by ONERA to us. The manuscript benefited from discussions and
critics of J.P. Véran, J. De Freitas Pacheco, G. Ricort and the GI2T team.


Up: Adaptive optics imaging of H
Copyright The European Southern Observatory (ESO)
![]() and
the observed data y(r) must then be dominated by statistical noise fluctuations,
with no bias term. In this relation, x(r) is our best reconstructed image, as shown in
Fig. 4, and h(r) the PSF 59 Cyg of Fig. 1 of the body of the paper.
We assume that the noise comes from a photo-detection process, and that y(r) is
a realization of the Poisson process of mean b(r).
and
the observed data y(r) must then be dominated by statistical noise fluctuations,
with no bias term. In this relation, x(r) is our best reconstructed image, as shown in
Fig. 4, and h(r) the PSF 59 Cyg of Fig. 1 of the body of the paper.
We assume that the noise comes from a photo-detection process, and that y(r) is
a realization of the Poisson process of mean b(r).