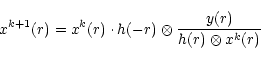 |
(1) |
The RL algorithm was then applied to these pre-processed images using the well-known iterative procedure:
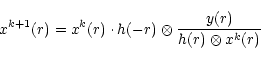 |
(1) |
 |
Figure 4:
Reconstructed image of P Cyg with the RL algorithm stopped at
iteration 245. Top: Representation in gray levels in a linear scale. Bottom:
Representation in contour plot. Contours levels are not equally spaced and correspond to:
100, 80, 60, 40, 30, 15, 12.5, 9, 6.5, 5, 3.5, 2, 1.2 percent of the
image's maximum. North is at the top and East is at the right of the
images. This corresponds to a rotation of 104.7 |
To limit the instability that appears in the solution, due to the amplification of noise, we stop the iteration number by using a comparison between the Fourier Transform of the reconstructed object at the iteration k and the Fourier transform of the image reconstructed by a Wiener filter ([Lantéri et al. 1998]; [Lantéri et al. 1999]). The main difficulty is then shifted to a correct determination of the Wiener filter. The comparison led us to choose an iteration number of 245. The result of the deconvolution is given both in grey levels and in a contour plot in Fig. 4. To make the envelope clearly visible, the contour levels are not equally spaced. The general pattern is that of a bright star, not resolved by the 152 cm telescope, surrounded by an extended envelope with bright spots.
These same
results were obtained with the reconstruction RL
algorithm regularized by a Tikhonov term, and in particular using the
Laplacian operator ([Lantéri et al. 1999]). The result of this deconvolution is presented in
Fig. 5 for the iteration 250 with a regularization factor equal to 0.01.
| |
Figure 7: Representation at the same scale of the reconstructed image of the Fig. 5 (left) and of the PSF (right) in contour plot. The white parts are due to the threshold and the saturation applied to both images: intensities lower than 6% and higher than 15% of the maximum are made white. North is at the top and East is at the right of the images |
We may conclude from this first analysis that the envelope of P Cyg is well resolved by the central core of the PSF of the 1.52 m telescope, corrected by the adaptive optics system. However, the envelope remains comparable in size with the residual halo of the PSF. This assumes at least that we are free of anisoplanatism problems ([Fusco et al. 2000]); this absence of variation allows the use of conventional deconvolution methods.
The question then may arise whether some of the fine structures we discovered in this envelope may be due to artifacts of the reconstruction process. A very important issue to consider, is a possible variation of the PSF during the experiment (from P Cyg to 59 Cyg), as discussed recently by Harder and Chelli ([Harder & Chelli 2000]). These authors show that a local non-stationary turbulence may produce strong residual aberrations (clearly visible in the first diffraction ring of their Fig. 17). At worst, we can imagine that the observed structures in our image result only from variations in the PSF, from P Cyg to 59 Cyg.
A comparison between the reconstructed image and the PSF is made
in Fig. 7. To make the structures more visible, we used a representation
similar to that of Harder and Chelli ([Harder & Chelli 2000]). The images are negatives of
intensities and the representation uses threshold and saturation. Doing so, a strong (white)
secondary maximum appears in the image of P Cyg, and two lower ones remain far away from the
core. Moreover, Fig. 7 shows clear evidence that the central (white) surface
of the reconstructed object is larger than that of the PSF (this will be interpreted in the
next section as an effect of the envelope).
Such a
structured image can hardly result from the variations of the PSF. However, it is also difficult
to ascertain that our reconstructed image is free of any residual error (much more data
would have been necessary for this). To strengthen our confidence in the fine details of
the reconstructed image of the envelope, we have implemented a series of
tests and processings.
They are described in Sects. 3.2 and 3.3, and in the Appendix.
 |
Figure 8:
Representations in grey levels of the residual blurred envelope
|
We then processed the residual blurred envelope
![]() using the same RL algorithm stopped at the same iteration number
245. The result is depicted both in grey levels and in a contour plot with
linear contour spacing in Fig. 9.
The image of the envelope is fully consistent with what was obtained in the raw deconvolution of Fig. 4.
The bright spots are all found at the same position. Moreover, there
is a bright spot very close to the star clearly visible in this
representation in the South-West direction; it was only perceptible as a small deformation of the central star in Fig. 4.
using the same RL algorithm stopped at the same iteration number
245. The result is depicted both in grey levels and in a contour plot with
linear contour spacing in Fig. 9.
The image of the envelope is fully consistent with what was obtained in the raw deconvolution of Fig. 4.
The bright spots are all found at the same position. Moreover, there
is a bright spot very close to the star clearly visible in this
representation in the South-West direction; it was only perceptible as a small deformation of the central star in Fig. 4.
In respect to this we may conclude that the deconvolution was carried out taking into account the problem of noise; we also made use of an a priori model, by assuming that P Cyg was the sum of an unresolved star and an envelope. An important question remains: up to what precision can we trust 59 Cyg as an accurate PSF for P Cyg? Several elements enable us to give a positive answer to that question: the seeing conditions were similar for both observations, and we found the same ratio of the flux envelope/star (about 4) before and after deconvolution. It would have been very convincing to have a series of sandwitched observations of P Cyg and a reference, eventually with different seeing conditions, and have all the results that converge towards a unique solution. In fact, we made an elementary test that consisted in dividing the long exposure of P Cyg in two sequences. The same operation was applied to 59 Cyg. We have then made a deconvolution of these four resulting images. The results are very similar to those obtained with the deconvolution presented in Fig. 4 and are not reproduced here. In an alternative we give in the appendix the results of a series of additional tests that tend to confirm 59 Cyg as a correct PSF.
We believe we have interpreted our current data as far as is possible. Of course, future observations, with possibly a larger telescope, will be very useful to confirm our first results and to further specify the morphology of this object.
Copyright The European Southern Observatory (ESO)