5 Numerical simulations

5.1 Test with variable PSF

5.1.1 The simulated images

To check the ability of the method to reconstruct the spatial variations of the kernel, a series of tests were performed with simulated images. The images are generated by putting stars randomly in the image, with a magnitude distribution corresponding to a bulge luminosity function. Noise is added in the images according to Poisson statistics. For the reference image we take a constant Gaussian PSF:

$$\Phi_{0}(u,v) = {\rm e}^{-\alpha(u^2+v^2)}.$$

In our simulation we take $\alpha=0.5$.

For the other image we simulate a variable PSF by taking the sum of 2 Gaussians with different widths and a relative weighting which is a function of the position in the image. We also introduce a normalization factor for conservation of the flux.

$$\Phi(u,v) = \frac{{\rm e}^{-\alpha(u^2+v^2)} + r(x,y) \times {\rm e}^{-\frac{\alpha(u^2+v^2)}{4}} }{1+4 \ r(x,y)}\cdot$$

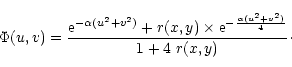
For the spatial variation we take:

$$r(x,y) = \frac{0.25 \ y}{w}\cdot$$

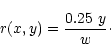
Where w is the size of the simulated image.

The resulting images are presented in Fig. 1.

5.1.2 Image subtraction

First, a subtracted image with constant kernel solution was constructed. We used a set of parameters for the kernel similar to Alard & Lupton (1998). For the fit with variable kernel solution we used a polynomial of order 2, since the variations of the coefficients of the PSF function are nearly parabolic. The resulting subtracted images are presented in Fig. 2.

5.1.3 Noise estimation

Noise in the subtracted image has 2 origins, the noise in the image to fit, and the noise in the reference image convolved with the kernel solution.

In our images the Poisson noise can be extremely well approximated locally by a Gaussian distribution with $\sigma=\sqrt{N}$. However this is not true for the reference image, since it has been transformed by convolution. The noise in the convolved image can nonetheless be estimated in a straightforward way. The convolution will result in the combination of different Gaussian distributions, with different $\sigma$s and weights. Using the same notation where I is the image to fit and R is the reference image, we now define the IC to be the reference image convolved with the kernel solution,

$$IC_i = \sum_j R_{i-j} \ K_j.$$

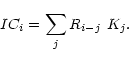
The combination of the two Gaussian distributions will result in a Gaussian distribution, and the resulting $\sigma$ of the distribution can be estimated by calculating the variance:

$$\sigma_i^2 = \sum_j {\rm var}(R_{i-j}) \ K_j^2 = \sum_j R_{i-j} \ K_j^2.$$

Thus we see that the local variance of the image can be estimated by convolving the image with a filter that is just the square of the initial convolution filter. Consequently we define a Poisson deviation as:

$$\delta = \sqrt{\sigma_i^2 + I_i}.$$

The histograms of the pixels in the subtracted images normalized by the Poisson deviation are presented in Fig. 3. It is interesting to note that order 2 is sufficient to produce a $\chi ^2$ per degree of freedom ( $\chi^2/{\rm Dof}$) which is extremely close to 1.

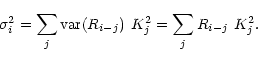
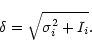
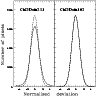Figure 5: Histograms of the normalized deviations in the subtracted images presented in Fig. 4. Left is the histogram for constant kernel solution, and right is the histogram for a fit of kernel variation to order 2. The dashed curve is Gaussian with $\sigma =1$. Note the goodness and the dramatic reduction of the $\chi ^2$ when fitting the kernel variations

Figure 6: Histograms of the deviations in the subtracted image in the case of very undersampled PSF's. The PSF in the reference image is very narrow with: FWHM = 1.17 pixels, thus we are in presence of a bad case of under-sampling. For the other image FWHM = 1.67, consequently it is also under-sampled

5.2 Checking the ability of the method to correct the astrometric registration

Image registration is performed by calculating a polynomial transform from the positions of bright objects. However, there is no guarantee that this procedure is optimal. In case the image registration to the reference frame is not perfect, a simple translation can be taken into account with a constant kernel solution. However more complex features like differential rotation, or differential distortion between the images cannot be corrected with constant kernel solution. But they can be corrected with non-constant kernel solution. We will illustrate this fact by simulating differential rotation between 2 images. We keep the reference image we had already generated for the previous simulations, and make another one by rotating the frames with respect to its center with an amplitude of 0.7 pixel from one corner to the other corner of the frame. The results of subtraction are presented in Fig. 4. The systematic pattern due to rotation appears clearly in the image with a constant kernel solution, while it is completely removed in the fit of a solution with a spatial variation of order 2. This is well confirmed by the $\chi ^2$ analysis which shows that an optimal result has been reached with the non-constant kernel solution (see Fig. 5).

5.3 Under-sampling

One last problem that can be encountered in astronomical images is under-sampling. To test the sensitivity of the method to under-sampling, we simulate a pair of very under-sampled images. We take $\alpha=2.0$ (FWHM = 1.17 pixels) for the reference and $\alpha=1.0$ (FWHM = 1.67 pixels) for the other image. Since our goal is just to test the effect of under-sampling only, we perform image subtraction with constant kernel solution. The resulting normalized $\chi ^2$ distribution is presented in Fig. 6. The result is as good as in the previous simulations. One may wonder why under-sampling does not induce any problems, since under-sampling should affect the convolution with the basis vectors. It is true that individually the least-square vectors which are obtained with under-sampled images will differ from the well sampled vectors. However one should not forget that the best solution is constructed by taking linear combinations of the least-square vectors. Even if the vectors are slightly different from the well sample vectors, an optimal linear combination of these vectors can still be made.

Figure 7: Left is the subtracted image obtained with constant kernel solution. Note the systematic residuals around the bright objects on the left side of the image and in the upper right corner. Note the diseaperance of these pattern in the next image, which has been obtained by fitting the spatial variations of the kernel to order 2. Two variables are present in the field (the bright and dark spots), and circular areas around these objects had to be excluded for $\chi ^2$ evaluation