4 Imposing constant flux scaling

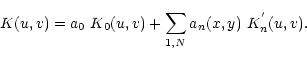
In practical applications, we expect the flux scaling factor between the 2 images being matched to be constant. As a result of the large number of degrees of freedom, the flux scaling factor, which is the sum of the local kernel, in general will not be constant. This will lead to imperfect flux conservation. Since flux conservation is extremely important for photometry, it is essential to add this constraint to the fit.

Least squares fitting with constraints is not always easy to implement. In this case the constraint will be that the sum of the kernel be constant at all points of the image. By using the derivative of the sum one may solve this problem by the technique of the Lagrange multipliers. However, in this case the number of Lagrange multipliers will be close to the number of basis vectors used to model the spatial variations. Thus it would require solving a large number of additional equations, and will not be very efficient.

Fortunately, there is a more elegant way to solve this constraint. One can always consider using a new basis of vectors for the kernel that are linear combinations of the previous vectors. We can construct the new set in such a way that all basis vectors, except the first one, have zero sums. Some of the vectors will already have zero sums, and we will keep them unchanged. For the others, except the first one, we make the combination:

K_n^' = K_n-K₀.

Provided the vector K_n are normalized, the vectors K_n^' will all have zero sums except K₀^' which will be equal to K₀.

Then all we have to do is expand in image coordinates all the coefficients of the kernel expression, except the first coefficient. It will result in the following kernel formula:

$$K(u,v) = a_0 \ K_0(u,v)+\sum_{1,N} a_n(x,y) \ K_n^{'}(u,v).$$

One can easily check that such a kernel has a constant sum, since all vectors whose coefficients depend upon x and y have zero sums.

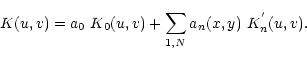
Of course, this method can be used to calculate, with a minimum number of operations, the global matrix from the zero order matrix. In practice this method gives very good numerical conservation of the kernel sum, this is an important asset making the method more robust and more accurate.

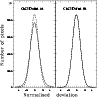Figure 3: Histograms of the normalized deviations in the subtracted images presented in Fig. 2. Left is the histogram for constant kernel solution, and right is the histogram for a fit of kernel variation to order 2. The pixels in the subtracted images have been normalized by the Poisson deviations (see text for details). The dashed curve is Gaussian with $\sigma =1$

Figure 4: Left is the subtracted image obtained with constant kernel solution. Note the systematic pattern due to the differential rotation between the images. Next is the subtracted image obtained by fitting the spatial variations of the kernel to order 2. Note the complete disappearance of the systematic patterns