3 Solving for space-varying kernel solution with minimum computing time

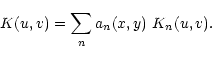
Most of the computing time involved in the computation of the kernel solution is spent in the calculation of the least-square matrix. The solution of the linear system itself takes an almost negligible amount of time. The computing time to build the matrix goes like the square of the number of coefficients. Thus the problem is that if we introduce new coefficients in order to fit the kernel variations, the cost of the calculation will quickly become prohibitive. To be more specific, let's derive analytical formulae for the spatial variations of the kernel. At each position (x, y) we can develop the kernel on the basis functions K_n. Thus the coefficients a_n will be functions of (x, y). Consequently the kernel can be written:

$$K(u,v) = \sum_n a_n(x,y) \ K_n(u,v).$$

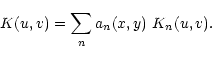
We assume that the coefficients a_n are smooth function of x and y. For simplicity we adopt a polynomial function of degree d₁.

$$a_n(x,y) = \sum_{i,j} b_{i,j} \ x^i \ y^j.$$

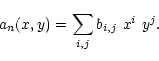
The relevant least-squares vectors are:

$$V_n(x,y) = \ W_m(x,y) \times P_q(x,y)$$

with:

$$W_m(x,y) = \frac{[R \otimes K_m](x,y)}{\sigma(x,y)}$$

$$P_q(x,y) = x^i \ y^j$$

and:

$$q = i+j \times d_1$$

$$nc_1 = \frac{(d_1+1)(d_1+2)}{2}$$

$$n = q\ + \ m\times nc_1.$$

The elements of the least-squares matrix can be expressed as scalar products of the least-squares vectors:

$$M_{n1,n2}=\int W_{m1}(x,y)W_{m2}(x,y)P_{q1}(x,y)P_{q2}(x,y){\rm d}x {\rm d}y.$$

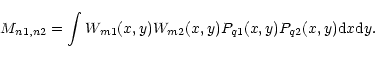
The above integral extends over the entire image. However, we can always divide the integration domain into small rectangular sub-areas. Within each small area, one can assume that the kernel is constant. It corresponds to approximating x and y by the coordinates of the centers of the sub-areas, (x_k, y_k).

The matrix elements can then be written:

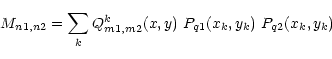$$M_{n1,n2} = \sum_k Q_{m1,m2}^k(x,y) \ P_{q1}(x_k,y_k) \ P_{q2}(x_k,y_k)$$ (3)

with the following definition for the integral in the rectangular domain D_k:

$$Q_{m1,m2}^k = \int_{D_k} W_{m1}(x,y) \ W_{m2}(x,y) \ {\rm d}x {\rm d}y.$$

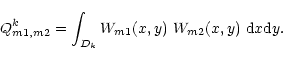
A similar method can be applied to expand the vector on the right hand side of Eq. (2).

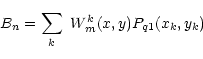$$B_n = \sum_k \ W_m^k(x,y) P_{q1}(x_k,y_k)$$ (4)

with:

$$W_m^k(x,y)= \int_{D_k} I(x,y) \ \frac{W_{m1}(x,y)}{\sigma(x,y)} \ {\rm d}x{\rm d}y.$$

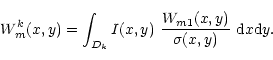
We see that the matrix elements corresponding to fitting the spatial variations of the kernel can be deduced from the matrix elements Q_m1,m2^k for only the cost of a summation over the number of sub-areas. The matrix Q_m1,m2^k, corresponds to the constant kernel solution, and has a much smaller number of elements than the matrix M_n1,n2^k. Once Q_m1,m2^k has been estimated, M_n1,n2 can be calculated using the expansion given in Eq. (3). This procedure results in a drastic economy in computing time, since the summations inside the individual sub-areas are avoided for the calculation of the matrix elements. Using Eq. (4) the same type of expansion applies also to the calculation of the vector B_n. Since the individual sub-areas should be slightly larger than the kernel, a typical number for the surface of a sub-area is $30\times30$ pixels. It means that in computing application we make a saving of about a factor 1000 in the calculation of the matrix elements of the matrix M_n1,n2 which corresponds to the spatial variations. In practice, fitting the kernel variations costs only about 20% more than making a constant kernel fit.

In high sparse fields, e.g. at high latitudes, the only useful areas are those centered on bright (high S/N) objects. It usually results in a drastic reduction in the number of pixels to fit. Even in crowded fields, most of the information is contained in some high density regions. Thus in practice the fit can be restricted to a fraction of the image.