

Up: Intraday variability in compact
Subsections
2 Observations and data reduction
Table 1:
Summary of the observing campaigns. The number in the
last column gives the number of flat-spectrum sources observed; i.e., the
steep-spectrum calibrators are not included in these figures
| date |
array configuration |
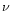 [GHz]
[GHz] |
number of sources |
| May 4, 1989 - May 9, 1989 |
full array, B
 B/C-reconfiguration B/C-reconfiguration |
0.33, 1.49, 4.86, 8.44, 15.0 |
9 |
| Jan. 29, 1990 - Feb. 23, 1990 |
sub-array, 5 antennae |
1.49, 4.86, 8.44, 15.0 |
3 |
| Oct. 2, 1992 - Oct. 23, 1992 |
sub-array, 5 antennae |
1.49, 4.86, 8.44 |
10 (+2 stars) |
The dates of the observations, the array configurations, and the observing
frequencies are listed in Table 1. For the first experiment we used
the full VLA for about 5 days. The array was divided into two similar
sub-arrays; one of them was used for observations at 0.33GHz, 1.49, and
4.86GHz, the other at 8.44 and 15.0GHz. Both other campaigns were made
during ongoing D
 A reconfiguration times of the VLA with sub-arrays
of five antennae for periods of three to four weeks. Since the information from
our observations with a five-antenna subarray was insufficient for polarization
calibration
A reconfiguration times of the VLA with sub-arrays
of five antennae for periods of three to four weeks. Since the information from
our observations with a five-antenna subarray was insufficient for polarization
calibration![[*]](/icons/foot_motif.gif) , we could obtain reliable polarization information only for the
first experiment. The data at 0.33GHz turned out to be heavily affected by
interference and confusion problems, and could not be meaningfully searched for
variability.
, we could obtain reliable polarization information only for the
first experiment. The data at 0.33GHz turned out to be heavily affected by
interference and confusion problems, and could not be meaningfully searched for
variability.
The observational procedure was as follows: Every source was observed for
approximately five minutes per frequency, then we changed to another source. At
regular intervals, we included non-variable steep-spectrum sources (1311+678
and 1634+628) to monitor and correct for any elevation-dependent and
time-dependent effects (this procedure had successfully been used before in IDV
observations at the 100m telescope, cf. Heeschen et al. 1987;
Quirrenbach et al. 1989a). In addition, the steep-spectrum sources are useful to determine
the measurement errors, since they do not show any genuine variations on short
timescales (Heeschen et al. 1987).
The primary data are 10s outputs from the correlator for each antenna pair,
separately for the four polarization combinations (RR, LL, RL, and LR), and two
adjacent 50MHz IF bands. For the calibration, as a first step, erroneous
10s intervals were eliminated. Hereafter, we have not followed the usual data
analysis procedures for VLA observations, since amplitude self-calibration
would level out the variations we have been looking for. Since for sources
dominated by a strong point-like core - as are most of the sources observed
here - the phase is zero by definition, we have performed phase
self-calibration for every source first. Subsequently, a (one-day) mean
amplitude gain factor has been derived using non-variable sources like
1311+678, which were linked to an absolute flux density scale (Baars et al. 1977;
Ott et al. 1994) by frequent observations of the primary calibrators
3C286 and 3C48. The choice of a constant amplitude gain factor for each
one-day block of data has the advantage that systematic amplitude changes are
not leveled out and can be corrected more precisely later.
During the first few hours of the May 1989 observing run, we observed the field
around each source with the full array in B configuration. Maps of the sources
were obtained from these data with standard VLA data reduction procedures,
including full self-calibration and Högbom cleaning. The clean components
corresponding to extended emission or confusing sources (i.e., all clean
components but those at the origin of the image plane) were Fourier transformed
back into the uv plane, and subtracted from the measured visibilities. (We
assume that the flux density in the outer components does not show any
significant variations.) This procedure isolates the pointlike cores of the
sources. Thus, we have been able to avoid systematic artificial variations due
to extended structure without losing any data (as would happen by simply
discarding data outside a limited uv range). Extended structure has to be taken
into account for 0716+714, 0836+710, 0954+658, 1642+690, and 1928+738 at
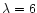 cm, and for 0716+714, 1642+690, 1928+738, and 2007+777 at
cm, and for 0716+714, 1642+690, 1928+738, and 2007+777 at
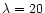 cm. Corrections for confusing sources within the field-of-view
were made for 0917+624 and 0954+658.
cm. Corrections for confusing sources within the field-of-view
were made for 0917+624 and 0954+658.
After this correction and a second pass of editing spurious sections of the
data, each five-minute scan was incoherently averaged over time, baselines,
polarization (RR and LL), and IF bands. Due to the point-like structure of the
sources (after our structure correction where necessary), the mean correlated
flux density is equal to the core flux density. The flux density in the
extended structure was now added back to the data, to obtain the total flux
density of the source (and enable comparison to flux densities measured e.g. at the 100m telescope). Eventually, we removed spurious elevation-dependent
and time-dependent effects in the light curves, using correction functions
derived from observations of the non-variable sources 0836+710, 1311+678, and
1634+628.
The errors are composed of the statistical errors from the averaging and a
contribution from the residual systematic fluctuations. The level of these
uncorrected residuals was determined from the apparent variations of the
calibrator source 3C286 and of the steep-spectrum sources. Typical standard
deviations were found to be in the range of 0.5% to 1.0% (depending on
the wavelength) of the mean value, with no significant difference between the
individual non-variable sources. Only for the 2cm data was the standard
deviation significantly higher, about 1.3% to 2%.
For the polarization data (experiment in May 1989) we performed phase and
amplitude calibration as described above. The Stokes parameters Q and Uwere derived from the cross correlation between the LHC and RHC polarizations,
with gain factors carried over from the analysis of the total intensity data.
The circular polarization of these sources is negligible, cf. Weiler & de
Pater (1983). Q and U were then converted into polarized flux density Pand polarization position angle 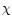 .
The source 0836+710 was used to
determine the instrumental polarization, assuming that its polarized intensity
and polarization angle are constant in time. In this case, the polarization
vector
.
The source 0836+710 was used to
determine the instrumental polarization, assuming that its polarized intensity
and polarization angle are constant in time. In this case, the polarization
vector
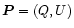 should describe a circle in the Q-U-plane around
the origin due to the parallactic rotation. The shift from the origin to the
actual center gives the vector of the instrumental polarization which was
subtracted from the measured polarization vector for all sources. A Faraday
rotation correction was applied to the data at
should describe a circle in the Q-U-plane around
the origin due to the parallactic rotation. The shift from the origin to the
actual center gives the vector of the instrumental polarization which was
subtracted from the measured polarization vector for all sources. A Faraday
rotation correction was applied to the data at
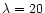 cm. Since the
global phase difference between LHC and RHC is unknown, all polarization angles
cm. Since the
global phase difference between LHC and RHC is unknown, all polarization angles
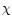 may be rotated by a constant value. This was calibrated with the main
calibrator 3C286 for which a polarization position angle of 33
may be rotated by a constant value. This was calibrated with the main
calibrator 3C286 for which a polarization position angle of 33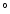 was
assumed at all wavelengths. Eventually, systematic effects were corrected using
the non-variable sources. The resulting errors were in the range of 3% to
5% for the polarized flux density and 3
was
assumed at all wavelengths. Eventually, systematic effects were corrected using
the non-variable sources. The resulting errors were in the range of 3% to
5% for the polarized flux density and 3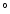 to 5
to 5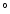 for the
polarization angle. It turned out that - in contrast to the total intensity
data - a significant fraction of the polarization data was very noisy. Most of
these data points have been
discarded, resulting in a sparser sampling for some
polarization light curves. For the sources 1749+701 (at
for the
polarization angle. It turned out that - in contrast to the total intensity
data - a significant fraction of the polarization data was very noisy. Most of
these data points have been
discarded, resulting in a sparser sampling for some
polarization light curves. For the sources 1749+701 (at
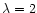 cm) and
1928+738 (at
cm) and
1928+738 (at
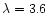 cm), we could not get any reliable polarization
data.
cm), we could not get any reliable polarization
data.


Up: Intraday variability in compact
Copyright The European Southern Observatory (ESO)