

Up: Intraday variability in compact
For the data analysis we use the modulation index m, which is
related to the mean flux density <S> and the rms flux density
variations 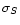 by
by
![\begin{displaymath}m {\rm [\%]} = 100 \cdot \frac{\sigma_S}{<S>}\cdot
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img26.gif) |
(1) |
It provides a measure of the strength of the variations observed, although it
does not take into account the error of the individual measurement. As a
criterion whether a source is variable or not, we perform a 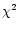 test with
test with
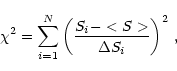 |
(2) |
where the Si are the individual flux densities and
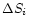 their
errors, e.g. Bevington & Robinson (1992). Actually, we determine the
probability that a constant function is a good fit to the data. Only sources
for which the probability that they can be fitted by a constant function is
their
errors, e.g. Bevington & Robinson (1992). Actually, we determine the
probability that a constant function is a good fit to the data. Only sources
for which the probability that they can be fitted by a constant function is
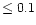 %, are considered to be variable.
%, are considered to be variable.
To compare the modulation indices at different wavelengths and epochs, and to
obtain a quantity that is independent of the measurement noise, we define the
variability amplitude for the variable sources as
![\begin{displaymath}Y {\rm [\%]} = 3 \sqrt{m^2-m_0^2}\, ,
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img31.gif) |
(3) |
where m0 is the modulation index of a non-variable source
(see Heeschen et al. 1987). The factor 3 is somewhat arbitrary, but
makes Y to be of the order of the peak-to-peak amplitude of the variations.
For the polarized intensity the corresponding quantities are
![\begin{displaymath}m_P {\rm [\%]} = 100 \cdot \frac{\sigma_P}{<P>}\, ,
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img32.gif) |
(4) |
![\begin{displaymath}Y_P {\rm [\%]} = 3 \sqrt{m_P^2-m_{P,0}^2}\, ;
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img33.gif) |
(5) |
and for the polarization angle we use
![\begin{displaymath}m_\chi {\rm [^\circ]} = \sigma_\chi,
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img34.gif) |
(6) |
![\begin{displaymath}Y_\chi {\rm [^\circ]} = 3 \sqrt{\sigma_\chi^2 - \sigma_{\chi,0}^2}\, \cdot
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img35.gif) |
(7) |
We note that this description of the polarization variability is somewhat
problematic because the polarization measurements are more strongly affected by
systematic effects than the total intensity data, and because the statistical
errors have a Gaussian distribution in the Stokes parameters Q and U, not
in P and 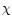 .
We have nevertheless chosen the above description, since the
separation of the variability of P and
.
We have nevertheless chosen the above description, since the
separation of the variability of P and 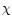 is more relevant for a physical
interpretation of the variations.
is more relevant for a physical
interpretation of the variations.
Structure functions can be used for the analysis of the characteristics of the
variability, and to search for typical timescales and periodicities. The first
order structure function 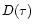 is defined as (see Simonetti et al. 1985):
is defined as (see Simonetti et al. 1985):
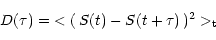 |
(8) |
with
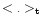 being the mean over time again. Since our data are unevenly
sampled, we derived the structure functions using an interpolation algorithm.
For any given time lag
being the mean over time again. Since our data are unevenly
sampled, we derived the structure functions using an interpolation algorithm.
For any given time lag 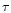 ,
the value of
,
the value of 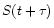 is calculated by linear
interpolation of the two adjacent data points. Each structure function was
derived twice, firstly starting from the beginning of the time series, and
secondly starting at the end and proceeding backwards. This provides a rough
assessment of the errors caused by the interpolation process (but not of the
systematic uncertainty due to the finite length of the observations).
is calculated by linear
interpolation of the two adjacent data points. Each structure function was
derived twice, firstly starting from the beginning of the time series, and
secondly starting at the end and proceeding backwards. This provides a rough
assessment of the errors caused by the interpolation process (but not of the
systematic uncertainty due to the finite length of the observations).
A typical timescale in the lightcurve (i.e., the time between a minimum and a
maximum or vice versa) is indicated by a maximum of the structure function,
while a period in the lightcurve causes a minimum of the structure function
(e.g. Heidt & Wagner 1996). Following the nomenclature of Heeschen et al.
(1987), structure functions can be used to define variability types, depending
on the observed timescale. A source whose structure function reaches a maximum
within the observing period is called type II (i.e., a fast-varying source). In
the case of a monotonically increasing structure function (i.e., when the
source shows no typical timescale less than the total observing period), it is
assigned type I. Since this definition is problematic for longer observing
campaigns as the ones in February 1990 and October 1992, we define a variable
source whose structure function reaches a maximum or plateau within
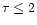 days as being of type II (cf. Wagner & Witzel 1995), otherwise type I.
Non-variable sources are assigned type 0.
days as being of type II (cf. Wagner & Witzel 1995), otherwise type I.
Non-variable sources are assigned type 0.


Up: Intraday variability in compact
Copyright The European Southern Observatory (ESO)
![]() by
by
![\begin{displaymath}m {\rm [\%]} = 100 \cdot \frac{\sigma_S}{<S>}\cdot
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img26.gif)
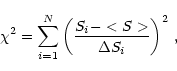
![\begin{displaymath}Y {\rm [\%]} = 3 \sqrt{m^2-m_0^2}\, ,
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img31.gif)
![\begin{displaymath}m_P {\rm [\%]} = 100 \cdot \frac{\sigma_P}{<P>}\, ,
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img32.gif)
![\begin{displaymath}Y_P {\rm [\%]} = 3 \sqrt{m_P^2-m_{P,0}^2}\, ;
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img33.gif)
![\begin{displaymath}Y_\chi {\rm [^\circ]} = 3 \sqrt{\sigma_\chi^2 - \sigma_{\chi,0}^2}\, \cdot
\end{displaymath}](/articles/aas/full/2000/02/ds1767/img35.gif)
![]() is defined as (see Simonetti et al. 1985):
is defined as (see Simonetti et al. 1985):
![]() days as being of type II (cf. Wagner & Witzel 1995), otherwise type I.
Non-variable sources are assigned type 0.
days as being of type II (cf. Wagner & Witzel 1995), otherwise type I.
Non-variable sources are assigned type 0.