Appendix B: Line-strength distribution with exponential cutoff.

In a number of publications related to the calculation of the line-force instability (e.g., Owocki et al. [1988], however also Gayley [1995]), a slightly modified version of the line-strength distribution function (10) has been used in order to prevent the instability from growing at wavelengths below the numerical grid resolution of order "Sobolev-length'' $L_{\rm S} = {v_{\rm th}}/({\rm d}v/{\rm d}r)$. To this end, an exponential cutoff at line-strength $k_{\rm max}$ has been introduced, where $k_{\rm max}$ can be considered as the maximum line-strength present or treated in the wind. Another argument for introducing this cutoff is given by the requirement of preventing the number of strong lines from becoming smaller than unity, i.e., only one line stronger than $k_{\rm max}$ shall be allowed to be present. The corresponding distribution - with otherwise constant exponent a - reads

$${\rm d}N(\nu, k_{\rm L}) = \,-\, N_{\rm o}\,f_{\nu}(\nu)\, k... ...\exp(-k_{\rm L}/k_{\rm max})\, {\rm d}\nu \,{\rm d}k_{\rm L},$$ (B1)

and the resulting line acceleration is modified by an additional factor

$$% latex2html id marker 4733 g({\rm cut}) {=} g_{\rm rad}^{\rm... ...m}{-}\left(\frac{k_{\rm 1}}{k_{\rm max}}\right)^{1-a} \right]$$ (B2)

which for $k_{\rm 1}/k_{\rm max}\rightarrow0$ approaches unity, of course. Note, that $k_{\rm 1}/k_{\rm max}= 1/\tau_{\rm max}$ relates to the maximum allowed optical depth per line at the considered depth point. It is interesting to investigate for this type of line-strength distribution the ratio of optically thick to total line-force, corresponding to our definition of $\hat \alpha$ in Sect. 2.4. For large values of $k_{\rm max}$, compared to $k_{\rm 1}$, this quantity should resemble the input value of a. However, for $k_{\rm 1}$approaching $k_{\rm max}$, differences are to be expected since the effective slope of the distribution function changes, becoming much steeper, until finally the number of optically thick lines vanishes and $\hat \alpha\rightarrow0$, as discussed below Eq. (22). Actually, this is what happens for realistic line distributions (cf. Fig. A1 and Sect. 4.2.8). In so far, this exercise provides some analytic understanding with regard to the behaviour of the effective $\hat \alpha$ value if either $k_{\rm 1}$ grows due to decreasing density or $k_{\rm max}$ decreases due to decreasing metallicity (cf. also Sect. 5).

Figure B1: Ratio of optically thick to total line-force ( $\approx \hat \alpha$) as function of $k_{\rm 1}/k_{\rm max}$ (cf. Eq. B3) and a = 0.7, 0.5, 0.3(fully drawn, dotted, dashed), for the line-strength distribution function with exponential cutoff, Eq. (B1). The triangles display the local $\alpha$-values derived from the line-distribution function itself, corresponding to the case of a = 0.5. Note, that $\alpha({\rm local}) < \hat \alpha$ as soon as (A2) becomes invalid. The small deviations between acceleration ratio and $\hat \alpha$ for small $k_{\rm 1}/k_{\rm max}$ are due to our approximation leading to Eq. (28)

If we calculate the optically thick line-force from (B1) by using a lower integration limit of $k_{\rm 1}$ as in (11), we obtain

$$\hat \alpha\,(k') \approx \frac{g_{\rm rad}^{\rm thick}}{g_{\rm rad}^{\rm tot}} =$$ (B3)

$$\frac{(1-{\rm e}^{-1})\,{\rm e}^{-k'} + (1+k')^{1-a} \Gamma(a... ...mma(a,k')} {\bigl( (1+k')^{1-a}\,-\,k'^{1-a} \bigr)\Gamma(a)}.$$

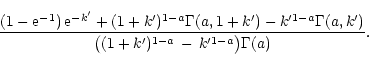
Note, that in this example $\hat \alpha$ depends only on the value of $k' = k_{\rm 1}/k_{\rm max}$ and the power-law index a, however not on the individual variables $k_{\rm 1}$ and $k_{\rm max}$. $\Gamma(a,x)$ is here related to the incomplete Gamma function via $\Gamma(a,x) = \Gamma(a) - \gamma(a,x)$. In Fig. B1, we have plotted $\hat \alpha$ as function of k' for three values of a = 0.7, 0.5 and 0.3. Obviously, for $k_{\rm 1}\rightarrowk_{\rm max}$ (or vice versa) the effective $\hat \alpha$becomes considerably smaller than the "input''-value, in agreement with our findings from Sect. 2.3.2. Note, however, that $\hat \alpha>0$ always and especially that it is much larger than the local $\alpha$ of the line-strength distribution function near $k_{\rm max}$!