Appendix A: A non-integral method, and its problems

An obvious alternative method for folding rotation curves can be described as follows: Suppose that U(r) denotes the estimated magnitude of velocities on the approaching arm whilst V(r) denotes the estimated magnitude of velocities on the receding arm, where r is the radial displacement from the estimated dynamical centre of the galaxy. Then, for an exactly known systematic velocity, $V_{{\rm sys}}$ and dynamical centre, $O_{{\rm dyn}}$, of a given galaxy, there is:

$$\sum^N_{i=1} \left(U(r_k) - V(r_k) \right)^2 = 0.$$

It follows that, in principle, rotation curves can be folded by minimizing the functional

$$F ~\equiv ~ \sum^N_{i=1} \left(U(r_k) - V(r_k) \right)^2$$

with respect to variations in $V_{{\rm sys}}$ and $O_{{\rm dyn}}$.

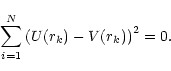
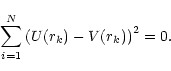
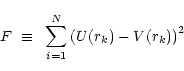
However, this method makes direct use of velocity and radial displacement measurements which are both intrinsically very noisy. By contrast, the Fourier method described in this paper is based on minimizing a functional defined over the Fourier coefficients A(m) which are estimated by integrating over the noisy velocity data - in other words, the method has an intrinsic smoothing mechanism incorporated within it. A recognized consequence of defining functions directly over noisy data is that they frequently fail to exhibit the mathematical properties of minimum points, even where such points are known to exist. In such a situation any minimizing algorithm designed to locate minimum points will fail. In the present case it is therefore to be expected that the functional F will frequently fail to exhibit the mathematical properties of a minimum point in the region of the actual $(V_{{\rm sys}}, O_{{\rm dyn}})$ solution.

In practice, when applied to the PS sample, the algorithm failed to find a sensible solution about 30% of the time. To illustrate this point, Fig. A1 shows the results of applying the algorithm to the ten rotation curves shown in Figs. 7 and 8. There are three total failures and one (71-G14) very poor solution. The remaining six solutions compare favourably with both the PS and the MK IV auto-folder solutions.

Figure A1: Solutions for the rotation curves of Figs. 7 and 8