| w(R1, R2, b1, b2) | = | (1) |
This section is dedicated to present the continuous form of the 2D wavelet approach we are later using to analyse discrete CMB maps. As a difference with the multiresolution approach used in Sanz et al. ([1999]) the 2D wavelet method provides information on many more resolution elements than the former method. Moreover, this property is crucial for performing an efficient linear denoising preserving the Gaussianity of the underlying CMB field (as will be discussed in Sect. 3.2).
The continuous wavelet transform of a 2D signal
f(x1, x2) is defined as
| w(R1, R2, b1, b2) | = | (1) |
| = | 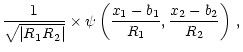 |
(2) |
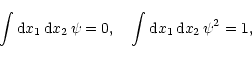 |
(3) |
and the "admissibility'' condition (that allows to reconstruct
the function f), i.e. there exists the integral
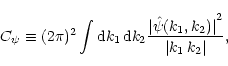 |
(4) |
where
![]() represents the 2D Fourier transform of
represents the 2D Fourier transform of ![]() and || denotes the modulus of the complex number.
and || denotes the modulus of the complex number.
A reconstruction of the image can be achieved with the inversion formula
| f(x1, x2) | = | 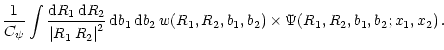 |
(5) |
| (6) |
Hereinafter, we shall consider 2D wavelets that are separable, i.e.
![]() .
In this case,
.
In this case,
![]() .
In particular, we
are interested in the Haar, the Mexican Hat and the Daubechies 2D-transforms
that can be generated in terms of the corresponding 1D wavelets. For
the Haar case, we find
.
In particular, we
are interested in the Haar, the Mexican Hat and the Daubechies 2D-transforms
that can be generated in terms of the corresponding 1D wavelets. For
the Haar case, we find
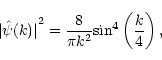 |
(7) |
with an absolute maximum at
![]() ,
whereas for the Mexican Hat
,
whereas for the Mexican Hat
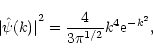 |
(8) |
with a single peak at
![]() .
The corresponding formulae
for the Daubechies wavelets of order N can be found in
Ogden ([1997]). The last
wavelets form an orthonormal basis with compact support,
increasing regularity with N and vanishing moments up to order N-1.
.
The corresponding formulae
for the Daubechies wavelets of order N can be found in
Ogden ([1997]). The last
wavelets form an orthonormal basis with compact support,
increasing regularity with N and vanishing moments up to order N-1.
Just as an illustration we would like to present the scalogram for a
CMB signal generated in a Standard Cold Dark Matter (SCDM) model.
Let us assume that the
image corresponds to a realization of a random field whose 2-point correlation
function is homogeneous and isotropic: ![]() ,
,
![]() .
This is equivalent to assume that the Fourier components
.
This is equivalent to assume that the Fourier components
![]() satisfy
satisfy
| (9) |
where P(k),
![]() ,
is the standard
Fourier power
spectrum and
,
is the standard
Fourier power
spectrum and
![]() means average value over realizations of the
field (the ergodicity of the field is assumed).
So, taking average values and using Eqs. (1) and (6), one obtains
the variance
means average value over realizations of the
field (the ergodicity of the field is assumed).
So, taking average values and using Eqs. (1) and (6), one obtains
the variance
![]() of the wavelet coefficients or scalogram
of the wavelet coefficients or scalogram
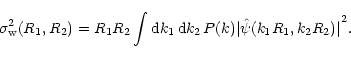 |
(10) |
For 2D white noise, i.e. P(k) =
constant, one gets that the scalogram,
![]() ,
is constant at any scale.
,
is constant at any scale.
On the other hand, if the field f represents the temperature
anisotropy of the CMB,
![]() ,
one can obtain
,
one can obtain
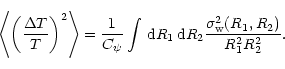 |
(11) |
In the top panel of Fig. 1
we have represented the scalogram
against the two scales R1 and R2 for SCDM using the Haar transform. The
qualitative behaviour for the other transforms is similar.
In the bottom panel we compare the scalogram along
the diagonal for standard, open
(
![]() )
and a flat-
)
and a flat-![]() (
(
![]() )
CDM models using the Haar and the Mexican Hat transforms. The
qualitative behaviour for the two transforms is similar: there is a plateau for
)
CDM models using the Haar and the Mexican Hat transforms. The
qualitative behaviour for the two transforms is similar: there is a plateau for
![]() and a maximum dependent on
and a maximum dependent on ![]() ,
corresponding to the first Doppler peak. Other secondary
maxima appearing in the figure are related to the secondary peaks in the
standard
,
corresponding to the first Doppler peak. Other secondary
maxima appearing in the figure are related to the secondary peaks in the
standard
![]() radiation power spectrum (the
radiation power spectrum (the ![]() is given by
is given by
![]() ).
Therefore, the position and amplitude
of the maxima that appear in the scalogram is model
dependent, being this quantity tightly related to the
).
Therefore, the position and amplitude
of the maxima that appear in the scalogram is model
dependent, being this quantity tightly related to the ![]() 's.
's.
Copyright The European Southern Observatory (ESO)