3 Data and other a priori information

3.1 Sampling

Our sample is made of the 154 Miras and 203 Semiregulars (34 SRa and 169 SRb) belonging to the HIPPARCOS Catalogue and for which mean values of both V and K magnitudes could be estimated. Their list is given in the Appendix B. For 257 stars, J was available too.

The selection of the LPVs to be included in the HIPPARCOS Input Catalogue (Mennessier & Baglin [1988]), and thus to be observed by the satellite, was based on the General Catalogue of Variable Stars [GCVS] (Kholopov et al. [1985], 1987) and on a criterium of visibility: only those stars that were visible (i.e. with an apparent magnitude below the HIPPARCOS magnitude limit, $m<m_{\rm lim}$) more than 80% of the time were included in the observation programme. This condition can be written as:

$$\frac{m_{\rm lim}-m_{\rm max}}{m_{\rm min}-m_{\rm max}}>0.8\,,$$

translating into a linear relationship $m_{\rm min}<a+b\; m_{\rm max}$. On the other hand, the amplitudes of the LPV stars lie within a certain range $A_{\rm min}\leq A\leq A_{\rm max}$. One can easily see in Fig. 1 that, with these criteria, all LPVs up to a certain magnitude $m_{\rm c}$ are selected and then, from $m_{\rm c}$ up to a limiting magnitude $m_{\rm lim}'$, the probability of selecting a star decreases linearly.

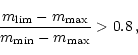
As said above, within the frame of the HIPPARCOS Catalogue, our sample only includes stars for which mean values of both V and K could be obtained. Thus, in any case, the only relevant selection effects (within the general frame of the GCVS) are related to the apparent magnitudes of the stars. In order to account for these combined effects, a selection function S(m) was introduced into the statistical model. Consistently with Fig. 1, it was defined so that all stars are selected up to a magnitude $\frak{m}_\frak{c}$ and then, up to a limiting magnitude ${\frak m}_{{\frak{lim}}}'$, the number of selected stars linearly decreases. The value of ${\frak m}_{{\frak{lim}}}'$ was taken equal to the apparent magnitude of the faintest star of the sample, and $\frak{m}_\frak{c}$ is determined (together with all other free parameters) by the LM method. In this way, the selection function adapts itself to the sample (and to each group that it contains, if several populations are assumed).

One must however remember that, despite the relatively large magnitude limit of the GCVS ( $V \simeq 15$, to be compared to the HIPPARCOS limit $\simeq 13$), the sample of Mira, SRa and SRb stars found therein is not necessarily complete at much lower magnitudes. Indeed, in case of poor data (a frequent problem with Semiregulars, according to Lebzelter et al. [1995]), it is difficult to detect the variability and to evaluate the amplitude and irregularity of the lightcurve. Then, stars may be missing in the GCVS, or SRa and SRb stars may be mistaken for each other or for Miras. There is also a significant probability to classify an SRa/b star as SR (no identified sub-type) or Lb (irregular variable), which two types were excluded from our study before applying the magnitude-based selection. On the other hand, due to their large amplitude and regularity, Miras are better identified; in the worst case, a Mira is simply mistaken for an SRb, but does not disappear from the sample. Summarizing, the boundaries of the three variability types considered in this study are more or less blurred, and the used GCVS sample is expected to be incomplete, especially concerning Semiregulars. In the previous edition of the catalogue, this had spectacular effects: the number of SRb stars dropped at $V\simeq 11$, instead of 15 for most other (sub-)types, including Mira, SRa and SR (Howell [1982]). Since then, however, the classification has sometimes been revised and many stars have been added. As far as we know, the actual incompleteness of the last edition of the GCVS has not yet been assessed. Nevertheless, one guesses that the probability of a star to have been insufficiently observed mainly depends on the apparent magnitudes at max and min and on the period (thus on the mean absolute magnitude). As a consequence, the magnitude-based, automatically adjusting selection function used in our statistical modelling should account for at least a significant part of the sampling bias introduced by the GCVS.

Figure 1: Principle of the selection function of the HIPPARCOS Input Catalogue (see text). The selected stars are located within the grey area

3.2 Astrometric data

For every star of the sample, the coordinates, the parallax and the proper motion were found in the HIPPARCOS Catalogue (ESA [1997]). The parallax is negative for 48 Miras, 6 SRa and 8 SRb, but the LM algorithm is, by design, able to handle and exploit it.

For 309 stars, radial velocities were found in the HIPPARCOS Input Catalogue [HIC] (Turon et al. [1992]). Only 23 Miras, 3 SRa and 22 SRb have no RV data.

3.3 Magnitudes

The photometric data that we have chosen are V (represented by visual measurements in this study), J and K magnitudes. K was chosen because, for LPVs, its behaviour mimics relatively well the one of the bolometric magnitude. The V-K colour is much more sensitive to the effective temperature and metallicity than J-K. On the other hand, the latter colour index is less affected by the presence of circumstellar dust shells, and it has the advantage that PLC relations using it have already been determined for the LMC. Simple simulations have shown that, for LPV lightcurves with realistic amplitudes, periods and asymmetries, the mean magnitude differs from the mid-point value (average of the magnitudes at maximum and minimum brightness) by at most a few 10^-1 in V and a few 10^-2 in K. We will thus use indifferently any of these two definitions in this study -- actually the mid-point value for V and the mean for K. Concerning the latter, it is worth noting that it also lies within less than 0.1 of the magnitude corresponding to the mean K flux.

For most Miras and for 10 Semiregulars, the adopted visual magnitudes at maximum and minimum light are mean values calculated by Boughaleb ([1995]) from AAVSO data covering 75 years (see Mennessier et al. [1997]). For 5 Miras, mean values of the max and min were deduced from AAVSO observations made during the whole HIPPARCOS mission. For 5 SR's, we used means at max and min derived from the last 3 decades of AAVSO data.

For 26 Semiregulars, we adopted the mean V magnitudes computed over decades by Kiss et al. ([1999]), using the Fourier transform.

For the remaining 28 Miras and for most of the Semiregulars, the visual magnitudes at max and min are the ones given by the HIC.

We remind that the magnitudes at maximum and minimum brightness given by the HIPPARCOS Input Catalogue are either averages over decades, found in Campbell ([1955]), or else estimated means derived from the GCVS (Kholopov et al. [1985], 1987). In the latter case, a statistical correction was applied to the catalogue values (and 1.5 mag subtracted in case of photographic magnitudes), as explained in the introduction of the HIC. For 4 Miras and 2 SRa's for which the HIC magnitudes were adopted, we were able to check their consistency (within 0.1 mag) with the 25-year means published by the AAVSO ([1986]).

The error bars of visual observations range from $\sigma=0.1$ to 0.5 mag according to the brightness. After binning and averaging, the precision at maxima is thus better than 0.1 mag; at minima, it may be worse. The derived mean magnitude is thus precise within about 0.2 mag. However, the uncertainty is larger for the mean maxima and minima derived from the GCVS extreme values: $\sigma=0.3-0.4$ mag according to our checking. Last, the error bars of the mean magnitudes derived by Kiss et al. ([1999]) are, of course, negligible compared to the former ones. We may thus state that the overall precision of the mean visual magnitudes used in this study is about 0.2 mag for Miras and 0.2-0.4 mag for Semiregulars.

J and K magnitudes (with individual error bars of few 10^-2 mag) were found in the Catalogue of Infrared Observations (Gezari et al. [1996]) -- which includes the large set of JHKL measurements of LPVs by Catchpole et al. ([1979]) and the measurements by Fouqué et al. ([1992]) -- and in recent papers: Groenewegen et al. ([1993]), Guglielmo et al. ([1993]), Whitelock et al. ([1994]), Kerschbaum & Hron ([1994]) and Kerschbaum ([1995]). The number of available data points per star ranges from 1 to more than 10, with an average of 1.5 for Miras and 2.2 for Semiregulars. As a consequence, considering the overall amplitude, which is usually mag but may reach 1.5 mag for Miras, the error bars ($\sigma$) of the mean magnitude are a few 10^-1 mag.

The mean colour indices V-K and J-K used in this study are the differences of the above defined mean magnitudes. The error bars are thus roughly 0.5 for the former and, since J and K measurements are usually made at the same phase, 0.1 mag for the latter.

Figure 2: Mean V-K colour versus period of the sample stars (raw data)

3.4 Periods

For 26 Semiregulars, mean periods computed over decades were taken from Kiss et al. ([1999]). For 21 other SR's, the periods were computed over tens of cycles by Bedding & Zijlstra ([1998]), Mattei et al. ([1997]), Percy et al. ([1996]) and Cristian et al. ([1995]).

For Miras and for the other Semiregulars, the adopted periods are the ones given by the HIC. Everytime possible (i.e. for nearly all Miras and for 10 SR's), we have checked that they are very close to the 75-year means calculated by Boughaleb ([1995]) from AAVSO data covering 75 years; the differences of a very few % correspond to the cycle-to-cycle fluctuations (see Mennessier et al. [1997]). For 4 Miras and 2 SRa's, we were able to check that the HIC periods lie within 1-2% of the 25-year means published by the AAVSO ([1986]). Concerning the other stars, we can only guess the overall quality of the HIC by checking all stars used by Kiss et al. ([1999]), Bedding & Zijlstra ([1998]), Mattei et al. ([1997]), Percy et al. ([1996]) and Cristian et al. ([1995]): for SRa stars, only 4% are found spurious (error ) and 83% are very good (error ); for SRb stars, about 25% of the HIC periods appear spurious and 66% very good.

As a consequence, about 15% of the periods may be spurious in the sample of Semiregulars used in this paper.

3.5 Constraints

In addition to these individual data, it is known that O-rich LPVs in the LMC follow linear mean relations between the absolute magnitude (M_K or $M_{\rm bol}$) and the logarithm of the period, and also near-infrared colour indices such as (J-K)₀ (Feast et al. [1989]; Hughes & Wood [1990]; Hughes [1993]; Wood & Sebo [1996]; Kanbur et al. [1997]; Bedding & Zijlstra [1998]). The existence of a linear {M_I, $\log P$} relation has also been shown (Feast et al. [1989]; Pierce & Crabtree [1993]). Moreover, Alvarez et al. ([1997]), applying to HIPPARCOS data an early version of the LM method that does not assume the existence of any PL or PLC relation, have shown that Oxygen-rich Miras in the solar neighbourhood do follow linear {$\log P$, M_K} relations. On the other hand, consistent with Kerschbaum & Hron ([1992]), a simple plot of our raw data (see Fig. 2) strongly suggests that Miras and Semiregulars are distributed around at least two linear {V-K, $\log P$} relations, the one of Miras being peculiarly well-defined.

As a consequence, the calibrations presented in this series of papers have been performed under the assumption (constraint) that there exist in the sample such PLC relations whose de-biased coefficients are to be calculated by the algorithm. The validity of this choice is confirmed by the consistency of the so-derived luminosities with the ones found without making this assumption (Mennessier et al. [1999]).

Figure 3: De-biased model period distributions (lines) and histograms of the data

   

Table 1: Model parameters of the four groups ($\theta$ denotes the fitted values and $\sigma$ their uncertainties)

	Group 1		Group 2		Group 3		Group 4
	$\theta$	$\sigma$	$\theta$	$\sigma$	$\theta$	$\sigma$	$\theta$	$\sigma$
U0 [km s-1]	-11.4	3.8	-33.8	5.9	-3.9	5.4	-33.1	66.2
$\sigma_U$	43.3	5.2	48.1	4.9	34.6	3.5	145.3	36.3
V0 [km s-1]	-31.9	5.0	-46.4	4.4	-19.1	1.8	-178.6	37.2
$\sigma_V$	29.8	2.0	37.9	4.5	17.5	3.3	102.4	26.3
W0 [km s-1]	-11.5	3.6	-10.8	5.1	-9.3	2.0	-4.8	30.6
$\sigma_W$	27.0	2.5	38.9	4.5	14.1	1.8	70.0	15.4
Z0 [pc]	368	55	476	54	174	28
$\overline{\log P}$	2.48	0.01	2.00	0.06	1.75	0.06	2.24	0.03
$\sigma_{\log P}$	0.04	0.01	0.27	0.03	0.29	0.02	0.06	0.01
$\overline{(V-K)_{0}}$	8.47	0.11	5.75	0.13	6.19	0.28	5.56	0.46
$\sigma_{(V-K)_{0}}$	0.52	0.04	1.04	0.09	1.14	0.08	0.86	0.17
Cor. $(\log P,(V-K)_0)$	-0.85	0.04	-0.46	0.07	-0.65	0.06	-0.49	0.44
$\frak{m}_\frak{c}$	-4.0	2.4	-2.7	1.6	-4.0	1.3	1.8	1.5
%	31.8	0.02	29.3	0.03	34.9	0.03	3.9	0.02