

Up: Détermination des rayons de Céphéides
Subsections
L'effet Doppler observé, dû au déplacement radial de l'atmosphère de
l'étoile, n'est pas exactement la vitesse d'expansion 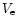 ,
mais la moyenne des
vitesses radiales intégrée sur tout l'hémisphère visible. La vitesse d'expansion
est évidemment la seule à considérer pour le calcul du déplacement.
L'intégration sur tout le disque conduit à une relation linéaire liant la vitesse
d'expansion à la vitesse radiale observée
,
mais la moyenne des
vitesses radiales intégrée sur tout l'hémisphère visible. La vitesse d'expansion
est évidemment la seule à considérer pour le calcul du déplacement.
L'intégration sur tout le disque conduit à une relation linéaire liant la vitesse
d'expansion à la vitesse radiale observée
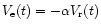 ,
où
,
où 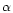 et le
facteur de projection (Imbert 1981a). Pour Coravel, la valeur de
et le
facteur de projection (Imbert 1981a). Pour Coravel, la valeur de
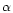 retenue est 1,36 (Burki et al. 1982; Burki & Benz
1982).
retenue est 1,36 (Burki et al. 1982; Burki & Benz
1982).
L'amplitude de variation du rayon de l'étoile sera donnée par
où t1 et t2 sont les deux instants du cycle de
pulsation où le rayon est extrémal, c'est-à-dire quand
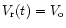 .
La théorie du mouvement dans un système double spectroscopique, exposée,
notamment par Binnendijk (1960), montre que
.
La théorie du mouvement dans un système double spectroscopique, exposée,
notamment par Binnendijk (1960), montre que
où
on peut ainsi calculer Z à chaque instant avec
Si P est exprimé en jours, K en km s-1, Z(t) s'exprime en rayons solaires par
Pour m mouvements, on peut alors calculer 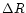 dans
le cas général avec
dans
le cas général avec
Pour chacune des étoiles nous
avons ainsi calculé les amplitudes de variation des rayons en utilisant les paramètres
des ajustements képlériens. Les résultats de ces calculs sont donnés dans le
tableau 3.
Pour l'époque t le rayon de l'étoile est calculé avec
où  est un rayon qui sera pris pour référence dans les calculs.
Dans le cas d'un seul mouvement, ce rayon est le rayon d'équilibre correspondant à une
accélération nulle. Nous avons montré (Imbert 1987), qu'à toutes les phases
de la pulsation on peut écrire une relation liant le rayon de l'étoile, la
magnitude et un indice de couleur. Avec les couleurs V et B, on peut écrire :
est un rayon qui sera pris pour référence dans les calculs.
Dans le cas d'un seul mouvement, ce rayon est le rayon d'équilibre correspondant à une
accélération nulle. Nous avons montré (Imbert 1987), qu'à toutes les phases
de la pulsation on peut écrire une relation liant le rayon de l'étoile, la
magnitude et un indice de couleur. Avec les couleurs V et B, on peut écrire :
a est le coefficient de proportionnalité entre 10 log 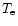 + CB et B-V (Imbert 1987).
En utilisant le déplacement
+ CB et B-V (Imbert 1987).
En utilisant le déplacement
on aura
![\begin{displaymath}V(t) = - 5~\log~[D(t) + R_{\rm c}] - a (B-V)(t) + Q.
\end{displaymath}](/articles/aas/full/1999/19/ds1717/img32.gif) |
(1) |
Pour chacune des époques des nbv observations de V et B-V on calcule D(t).
On dispose ainsi de nbv équations dont les inconnues à trouver sont a, Q et  .
Dans un premier calcul, on détermine une solution par moindres
carrés en linéarisant l'Éq. (1). En négligeant
.
Dans un premier calcul, on détermine une solution par moindres
carrés en linéarisant l'Éq. (1). En négligeant
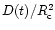 on est conduit à
on est conduit à
À partir de cette solution approchée, on détermine les vraies valeurs en résolvant
par approximations successives les équations de la forme
où
 sont respectivement la vitesse observée et la vitesse calculée. Après la
détermination de
sont respectivement la vitesse observée et la vitesse calculée. Après la
détermination de  il reste à formuler la différence entre le rayon moyen de
l'étoile,
il reste à formuler la différence entre le rayon moyen de
l'étoile,  ,
et
,
et  .
Le rayon moyen
.
Le rayon moyen  est défini par
est défini par
Dans
cette expression 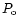 correspond au mouvement de plus longue période. Nous avons
montré (Imbert 1987), que pour un seul mouvement, avec les unités
utilisée plus hauts,
correspond au mouvement de plus longue période. Nous avons
montré (Imbert 1987), que pour un seul mouvement, avec les unités
utilisée plus hauts,
L'intégration étant linéaire, ce résultat se généralise
facilement au cas de plusieurs mouvements. On a ainsi :
![\begin{figure}\includegraphics[width=155mm]{1717f2.eps}\end{figure}](/articles/aas/full/1999/19/ds1717/Timg41.gif) |
Figure 2:
Vitesses radiales et ajustement par mouvements képlériens fictifs de TT Aql, RX Aur, SY Cas, CD Cyg, SZ Cyg, V402 Cyg, V1154 Cyg et AA Gem |
![\begin{figure}\includegraphics[width=155mm]{1717f3.eps}\end{figure}](/articles/aas/full/1999/19/ds1717/Timg42.gif) |
Figure 3:
Vitesses radiales et ajustement par mouvements képlériens fictifs de W Gem, BB Her, BL Her, BG Lac, RR Lac, Y Lac, SV Mon et UY Mon |
![\begin{figure}\includegraphics[width=155mm]{1717f4.eps}\end{figure}](/articles/aas/full/1999/19/ds1717/Timg43.gif) |
Figure 4:
Vitesses radiales et ajustement par mouvements képlériens fictifs de GQ Ori, RS Ori, AS Per, VX Per, ST Tau et SV Vul |
Pour la détermination des rayons, nous avons utilisé la photométrie UBV car,
pour les étoiles mesurées, cette photométrie réalise le meilleur compromis entre la qualité des mesures et la
proximité des observations avec nos mesures de vitesses radiales, condition essentielle pour ne pas biaiser les calculs
par une éventuelle dérive de la période. De plus, pour la plupart de nos étoiles, le nombre de mesures dans les
couleurs R, I, J ou K est très insuffisant pour la détermination des rayons.
Les résultats de ces calculs figurent dans le tableau 3.
Sur cet échantillon homogène mais partiel, car pour l'instant la zone de période 17 à
45 jours n'est pas encore couverte, nous avons calculé une
relation linéaire liant log P et log  .
.
BL Her, d'un type particulier, n'a pas été
considérée dans ce calcul. La relation entre log P et log  est
représentée sur la Fig. 1. Ce résultat est très proche, notamment, de celui
obtenu, avec V et B-V par Laney & Stobie (1995), qui donnent
est
représentée sur la Fig. 1. Ce résultat est très proche, notamment, de celui
obtenu, avec V et B-V par Laney & Stobie (1995), qui donnent
Cependant il y a désaccord avec les déterminations déduites d'autres couleur, notamment J et K. Il
semble que les couleurs J et K soient moins sensibles aux effets de variations de gravité ou de microturbulence
au cours de la pulsation. Laney & Stobie (1995) donnent une formule de correction au premier ordre pour tenir compte
de la variation de gravité. Si nous appliquons ces corrections à nos rayons nous déduisons la formulation suivante pour la relation période rayon :
Les coefficients restent néanmoins assez
différents de ceux de Laney et Stobie pour les couleurs J et K. Cette différence
doit, sans doute, être attribuée aux autres effets non pris en compte, tels que
microturbulence ou duplicité. On peut aussi se demander si avec les couleurs B et V,
le coefficient de projection et l'assombrissement centre-bord ne varient pas de manière plus significative au cours de la pulsation, et biaisent ainsi la détermination du rayon moyen.


Up: Détermination des rayons de Céphéides
Copyright The European Southern Observatory (ESO)
![]() ,
mais la moyenne des
vitesses radiales intégrée sur tout l'hémisphère visible. La vitesse d'expansion
est évidemment la seule à considérer pour le calcul du déplacement.
L'intégration sur tout le disque conduit à une relation linéaire liant la vitesse
d'expansion à la vitesse radiale observée
,
mais la moyenne des
vitesses radiales intégrée sur tout l'hémisphère visible. La vitesse d'expansion
est évidemment la seule à considérer pour le calcul du déplacement.
L'intégration sur tout le disque conduit à une relation linéaire liant la vitesse
d'expansion à la vitesse radiale observée
![]() ,
où
,
où ![]() et le
facteur de projection (Imbert 1981a). Pour Coravel, la valeur de
et le
facteur de projection (Imbert 1981a). Pour Coravel, la valeur de
![]() retenue est 1,36 (Burki et al. 1982; Burki & Benz
1982).
retenue est 1,36 (Burki et al. 1982; Burki & Benz
1982).

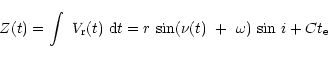
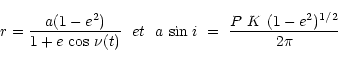
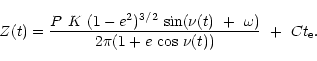
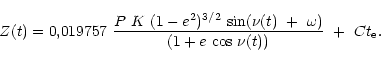
![\begin{displaymath}\Delta R = \alpha~ \left\vert
~\sum_m~[Z_m(t_{1m})~-~Z_m(t_{2m})]~\right\vert\cdot \end{displaymath}](/articles/aas/full/1999/19/ds1717/img27.gif)

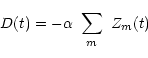
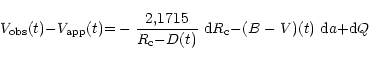

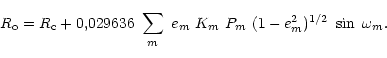
![\begin{figure}\includegraphics[width=155mm]{1717f2.eps}\end{figure}](/articles/aas/full/1999/19/ds1717/Timg41.gif)
![\begin{figure}\includegraphics[width=155mm]{1717f3.eps}\end{figure}](/articles/aas/full/1999/19/ds1717/Timg42.gif)
![\begin{figure}\includegraphics[width=155mm]{1717f4.eps}\end{figure}](/articles/aas/full/1999/19/ds1717/Timg43.gif)
![]() .
.