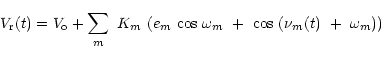
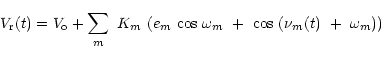
![]() étant défini par :
étant défini par :
avec
![]()
et
![]()
t est l'époque d'observation et Pm la période du mouvement m.
La valeur de m est un pour les Céphéides sans "bump'', deux pour les Céphéides avec "bump'', et, exceptionnellement trois quand deux mouvements ne suffisent pas à représenter correctement les observations (BL Her). Cet ajustement permet de représenter objectivement les observations de vitesse radiale en évitant les oscillations parasites introduites par un ajustement par développement de Fourier. Il permet en outre de maîtriser le nombre d'extremums de la courbe et donne une très bonne représentation de la pulsation, même dans le cas de mesures peu nombreuses ou mal réparties en phase. Toutes les formes de courbes rencontrées dans ce travail sont parfaitement représentées par ce lissage (Figs. 2, 3 et 4). Cette représentation analytique de la vitesse radiale de l'étoile au cours de sa pulsation est formellement identique à celle décrivant la variation de vitesse radiale des composantes d'un système double spectroscopique. On peut ainsi assimiler la variation de vitesse radiale d'une Céphéide à une somme de mouvements képlériens fictifs (Imbert et al. 1985; Imbert 1987; Imbert et al. 1989). Dans le cas de Céphéides doubles spectroscopiques, ces mouvements fictifs s'ajoutent au mouvement képlérien réel dû à la duplicité (Imbert 1994; Imbert 1996).
Les paramètres de lissage à calculer, ![]() ,
em,
,
em, ![]() ,
Km et
,
Km et
![]() ,
sont au nombre de 5, 9 ou exceptionnellement 13, auxquels s'ajoutent
éventuellement une, deux ou trois valeurs de Pm.
,
sont au nombre de 5, 9 ou exceptionnellement 13, auxquels s'ajoutent
éventuellement une, deux ou trois valeurs de Pm. ![]() est la vitesse du centre de
masse de l'étoile et Km l'amplitude de la composante m du mouvement. em et
est la vitesse du centre de
masse de l'étoile et Km l'amplitude de la composante m du mouvement. em et ![]() doivent être considérés comme des paramètres de forme.
doivent être considérés comme des paramètres de forme.
![]() est l'époque de passage au périastre de l'orbite fictive, mais ne correspond pas,
en général, à un instant remarquable dans la cycle de pulsation. Le calcul de
ces éléments orbitaux fictifs ou réels se fait par la méthode classique par
améliorations itératives des éléments approchés de départ. Tous les calculs
relatifs aux recherches de périodes, détermination des éléments orbitaux approchés
et amélioration de ceux-ci par la méthode de moindres carrés de
Schlesinger (1908), ont été effectués avec le programme SB5MCEX écrit en VBA Excel
et mis en
est l'époque de passage au périastre de l'orbite fictive, mais ne correspond pas,
en général, à un instant remarquable dans la cycle de pulsation. Le calcul de
ces éléments orbitaux fictifs ou réels se fait par la méthode classique par
améliorations itératives des éléments approchés de départ. Tous les calculs
relatifs aux recherches de périodes, détermination des éléments orbitaux approchés
et amélioration de ceux-ci par la méthode de moindres carrés de
Schlesinger (1908), ont été effectués avec le programme SB5MCEX écrit en VBA Excel
et mis en ![]() uvre sur Power Macintosh. Ce programme, très
interactif, permet de rechercher les périodes (Imbert 1972), de calculer des éléments
approchés par une variante numérique de la méthode graphique de
Lehman-Filhès (1894), et de déterminer les éléments orbitaux définitifs
par itérations successives. Dans ce programme, il est possible de prendre en
compte jusqu'à cinq mouvements képlériens superposés. Le programme donne en outre
la possibilité de fixer n'importe quel élément à une valeur
prédéterminée, comme la période ou l'excentricité e. Les éléments orbitaux fictifs calculés
par la méthode ci-dessus sont donnés dans le tableau 2. Les
différences, O-C, entre la valeur observée et la valeur calculée
avec l'ajustement figurent dans le tableau 1.
uvre sur Power Macintosh. Ce programme, très
interactif, permet de rechercher les périodes (Imbert 1972), de calculer des éléments
approchés par une variante numérique de la méthode graphique de
Lehman-Filhès (1894), et de déterminer les éléments orbitaux définitifs
par itérations successives. Dans ce programme, il est possible de prendre en
compte jusqu'à cinq mouvements képlériens superposés. Le programme donne en outre
la possibilité de fixer n'importe quel élément à une valeur
prédéterminée, comme la période ou l'excentricité e. Les éléments orbitaux fictifs calculés
par la méthode ci-dessus sont donnés dans le tableau 2. Les
différences, O-C, entre la valeur observée et la valeur calculée
avec l'ajustement figurent dans le tableau 1.
| Période | nvr | m | e | K | ||||
| BL Her | 1,3074372 |
113 | 3 | 0,82 | 9,85 |
0,471 |
1,36 |
16,6 |
| 0,739 |
2,07 |
13,5 |
||||||
| 0,457 |
1,77 |
4,2 |
||||||
| UY Mon | 2,398255 |
30 | 1 | 0,47 | 34,09 |
0,301 |
1,84 |
9,7 |
| ST Tau | 4,034299 (*) | 32 | 1 | 0,73 | 1,11 |
0,412 |
1,67 |
18,0 |
| SY Cas | 4,071098 (*) | 43 | 1 | 0,79 | -46,93 |
0,408 |
1,67 |
18,2 |
| Y Lac | 4,323776 (*) | 43 | 1 | 1,12 | -22,25 |
0,388 |
1,63 |
18,6 |
| V402 Cyg | 4,364836 (*) | 32 | 1 | 0,68 | -13,42 |
0,351 |
1,53 |
15,2 |
| V1154 Cyg | 4,92546 (*) | 32 | 1 | 0,57 | -4,32 |
0,295 |
1,55 |
12,7 |
| AS Per | 4,972516 (*) | 20 | 1 | 0,55 | -30,39 |
0,473 |
1,55 |
19,9 |
| BG Lac | 5,331932 (*) | 31 | 2 | 0,34 | -18,02 |
0,415 |
0,86 |
17,1 |
| 0,133 |
2,37 |
5,6 |
||||||
| RR Lac | 6,41629 |
29 | 2 | 0,39 | -38,73 |
0,435 |
1,30 |
17,3 |
| 0,351 |
0,71 |
1,3 |
||||||
| BB Her | 7,50585 |
25 | 2 | 0,53 | 88,75 |
0,371 |
1,26
|
17,3 |
| 0,513 |
2,21 |
2,9 |
||||||
| RS Ori | 7,566881 (*) | 38 | 2 | 0,67 | 42,89 |
0,436 |
1,34 |
20,6 |
| 0,524 |
2,36 |
3,8 |
||||||
| W Gem | 7,91343 |
48 | 2 | 0,68 | 1,61 |
0,453 |
1,22 |
21,0 |
| 0,591 |
2,30 |
4,0 |
||||||
| GQ Ori | 8,61645 |
29 | 2 | 0,50 | 45,12 |
0,398 |
1,40 |
20,1 |
| 0,362 |
2,64 |
5,5 |
||||||
| VX Per | 10,8866 |
58 | 2 | 0,64 | -35,97 |
0,380 |
1,40 |
16,6 |
| 0,412 |
2,69 |
6,8 |
||||||
| AA Gem | 11,30334 (*) | 38 | 2 | 0,60 | 18,76 |
0,330 |
1,50 |
14,2 |
| 0,384 |
1,85 |
12,2 |
||||||
| RX Aur | 11,623537 (*) | 25 | 2 | 0,38 | -21,95 |
0,268 |
1,27 |
15,6 |
| 0,405 |
1,87 |
6,7 |
||||||
| TT Aql | 13,754707 (*) | 27 | 2 | 0,62 | 3,55 |
0,375 |
1,92 |
20,4 |
| 0,528 |
1,86 |
13,2 |
||||||
| SZ Cyg | 15,11034 (*) | 43 | 2 | 0,51 | -11,39 |
0,515 |
1,27 |
19,1 |
| 0,424 |
1,79 |
16,3 |
||||||
| SV Mon | 15,2342 |
40 | 2 | 0,56 | 27,32 |
0,481 |
1,63 |
23,8 |
| 0,554 |
1,89 |
14,8 |
||||||
| CD Cyg | 17,07414 (*) | 35 | 2 | 0,78 | -11,45 |
0,445 |
1,62 |
23,4 |
| 0,546 |
1,90 |
13,8 |
||||||
| SV Vul | 45,055 |
41 | 2 | 0,36 | -2,01 |
0,386 |
1,68 |
25,3 |
| 0,589 |
4,85 |
4,1 |
||||||
| Période | nbv |
|
a | |||
| BL Her | 1,31 | 69 | 12,3 | 11,7 |
1,24 |
2,48 |
| UY Mon | 2,40 | 25 | 35,9 | 35,3 |
1,18 |
2,56 |
| ST Tau | 4,03 | 55 | 46,3 | 44,7 |
3,55 |
2,29 |
| SY Cas | 4,07 | 96 | 50,9 | 49,3 |
3,63 |
2,26 |
| Y Lac | 4,32 | 34 | 56,0 | 54,2 |
3,98 |
2,33 |
| V402 Cyg | 4,36 | 85 | 47,9 | 46,4 |
3,33 |
1,96 |
| V1154 Cyg | 4,93 | 93 | 53,9 | 52,5 |
3,22 |
2,01 |
| AS Per | 4,97 | 44 | 54,1 | 52,1 |
4,67 |
2,44 |
| BG Lac | 5,33 | 84 | 50,7 | 48,8 |
4,30 |
2,21 |
| RR Lac | 6,42 | 192 | 63,9 | 61,6 |
5,19 |
2,17 |
| BB Her | 7,51 | 26 | 65,5 | 63,0 |
5,62 |
2,11 |
| RS Ori | 7,57 | 50 | 81,0 | 78,1 |
6,60 |
2,12 |
| W Gem | 7,91 | 60 | 66,9 | 64,2 |
6,55 |
1,95 |
| GQ Ori | 8,62 | 49 | 77,2 | 73,8 |
7,43 |
2,01 |
| VX Per | 10,89 | 62 | 95,7 | 91,1 |
8,98 |
2,19 |
| AA Gem | 11,30 | 90 | 93,5 | 87,7 |
10,19 |
1,90 |
| RX Aur | 11,62 | 45 | 96,1 | 91,2 |
9,25 |
1,98 |
| TT Aql | 13,75 | 60 | 100,5 | 91,4 |
16,7 |
2,19 |
| SZ Cyg | 15,11 | 48 | 106,8 | 97,4 |
17,7 |
2,18 |
| SV Mon | 15,23 | 192 | 111,6 | 100,8 |
20,2 |
2,11 |
| CD Cyg | 17,07 | 121 | 125,7 | 113,8 |
22,7 |
2,13 |
| SV Vul | 45,06 | 113 | 238,4 | 216,5 |
50,5 |
2,11 |
Copyright The European Southern Observatory (ESO)