

Up: Three stage period analysis
Subsections
A sample of n data points y(ti)
is fitted to a model
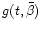 in our period search.
The Q free parameters are
in our period search.
The Q free parameters are
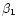 ,
,
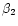 ,
...,
,
..., 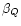 .
The most probable periodicity is searched for by determining
the absolute minimum for the sum of the squared residuals
.
The most probable periodicity is searched for by determining
the absolute minimum for the sum of the squared residuals
Let us assume that the model can be expressed as a linear sum
of separate model components
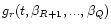 ,
which depend nonlinearly on the periods (frequencies) or other
parameters (e.g. decay rates, frequency shifts).
In this case the
RSS can be evaluated as a function
of the nonlinear parameters only,
because the linear parameters
,
which depend nonlinearly on the periods (frequencies) or other
parameters (e.g. decay rates, frequency shifts).
In this case the
RSS can be evaluated as a function
of the nonlinear parameters only,
because the linear parameters
 can
be estimated by ordinary regression methods for any fixed
set of nonlinear parameters
can
be estimated by ordinary regression methods for any fixed
set of nonlinear parameters
 .
This gives the Least Squares Spectrum
.
This gives the Least Squares Spectrum
where the linear parameter estimates
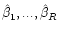 are also functions of the nonlinear parameters.
The
LSS minima reveal the most probable
nonlinear parameter combinations.
If the model is correctly specified,
the global
LSS minimum should give just the set of parameter
estimates searched for.
In this way the problem of model parameter estimation
can be converted to the problem of solving the global minimum or minima
of
LSS.
This approach has been applied to astronomical data already
by Vanicek (1969, 1971)
and Taylor & Hamilton (1972),
or more recently by
Martinez & Koen (1994),
Wilcox & Wilcox (1995) and
Bossi & La Franceschina (1995).
The
LSS analysis is not trivial for semirandomly
distributed observations,
like the astronomical data that often contain periodic gaps.
We formulate a flexible and computationally efficient approach to
this problem by dividing the analysis into several stages,
where the resolution of the spectra increases at each subsequent stage.
are also functions of the nonlinear parameters.
The
LSS minima reveal the most probable
nonlinear parameter combinations.
If the model is correctly specified,
the global
LSS minimum should give just the set of parameter
estimates searched for.
In this way the problem of model parameter estimation
can be converted to the problem of solving the global minimum or minima
of
LSS.
This approach has been applied to astronomical data already
by Vanicek (1969, 1971)
and Taylor & Hamilton (1972),
or more recently by
Martinez & Koen (1994),
Wilcox & Wilcox (1995) and
Bossi & La Franceschina (1995).
The
LSS analysis is not trivial for semirandomly
distributed observations,
like the astronomical data that often contain periodic gaps.
We formulate a flexible and computationally efficient approach to
this problem by dividing the analysis into several stages,
where the resolution of the spectra increases at each subsequent stage.
2.1 Multistage search
The first stage of the analysis, the Pilot Search,
provides crude estimates for the nonlinear parameters.
A standard Grid Search on a fine mesh centered at
these crude estimates is performed during the second stage.
Finally, traditional parameter refinement techniques are applied to
obtain the highest possible precision (Refined Search).
While the grid search and the refinement of the model parameters
represent commonly used astronomical data processing techniques,
the pilot search method is not so well known.
As a particular case of the general problem,
we consider the
LSS of the simple model
where the frequency f is the only nonlinear free parameter.
The linear free parameters for the mean (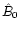 )
and the amplitudes
(
)
and the amplitudes
(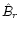 ,
,
 )
are functions of f.
The grid search over the full nonlinear parameter space
tests a discrete frequency set
)
are functions of f.
The grid search over the full nonlinear parameter space
tests a discrete frequency set
 ,
where
,
where
 and
and
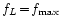 .
The chosen
fmin and
fmax limits may represent
the physically possible frequency range or some other interval of interest.
The fixed frequency step
.
The chosen
fmin and
fmax limits may represent
the physically possible frequency range or some other interval of interest.
The fixed frequency step  must be chosen carefully.
If the data cover an interval of
must be chosen carefully.
If the data cover an interval of
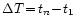 ,
it is reasonable constrain the maximum phase shift
,
it is reasonable constrain the maximum phase shift
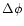 that
can occur within
that
can occur within 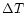 when any tested fl
changes by
when any tested fl
changes by  .
This gives
.
This gives
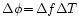 .
Sufficient values are
.
Sufficient values are
 ,
like the overfilling factor of
,
like the overfilling factor of
![$G\!=\![\Delta \phi]^{-1}\!\geq\!10$](/articles/aas/full/1999/18/ds1588/img65.gif) in Sect. 3.2.
Hence the corresponding number of tested frequencies
becomes
in Sect. 3.2.
Hence the corresponding number of tested frequencies
becomes
![$L\!=\!\Delta T
(f_{\mathrm{max}}\!-\!f_{\mathrm{min}}) [\Delta \phi]^{-1}$](/articles/aas/full/1999/18/ds1588/img66.gif) .
If the tested periods are much shorter than
.
If the tested periods are much shorter than 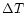 ,
then L becomes large.
Having fixed
,
then L becomes large.
Having fixed
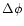 ,
one can reduce L by shortening
,
one can reduce L by shortening
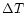 or
or
 .
The following general scheme of a simple multistage
search reduces
.
The following general scheme of a simple multistage
search reduces 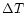 on the first,
and
on the first,
and
 on the second stage,
respectively.
on the second stage,
respectively.
- 1.
Divide the data into
k separate
parts with a length
of
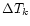
.
Compute the
LSS spectrum within each part using a frequency
step
![$\Delta f_{\mathrm{crude}}\!=\!
\Delta\phi[\Delta T_k]^{-1}$](/articles/aas/full/1999/18/ds1588/img69.gif)
,
i.e. the number of tested frequencies is
![$L_k\!=\!\Delta T_k
(f_{\mathrm{max}}\!-\!f_{\mathrm{min}}) [\Delta \phi]^{-1}$](/articles/aas/full/1999/18/ds1588/img70.gif)
.
Use the average of all spectra for obtaining the crude periodicity
estimates.
- 2.
Compute the fine grid search spectra for all data
within narrow frequency intervals centered at these crude estimates.
Apply a frequency step of
![$\Delta f_{\mathrm{fine}} \!=\! \Delta \phi [\Delta T]^{-1}$](/articles/aas/full/1999/18/ds1588/img71.gif) .
A suitable width for the tested frequency interval
is about
.
A suitable width for the tested frequency interval
is about
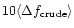 ,
where
,
where
 is
the mean frequency step that was used during the 1st stage.
With this particular width, the number of tested frequencies is
is
the mean frequency step that was used during the 1st stage.
With this particular width, the number of tested frequencies is
![$L \!=\! 10 \Delta T \Delta f_{\mathrm{crude}} [\Delta \phi]^{-1}$](/articles/aas/full/1999/18/ds1588/img74.gif) .
.
- 3.
Refine the precision of the frequency estimates
with the standard Marquardt iteration
(see e.g.
Press et al. 1988).
The simplest multistage search techniques were
first described by Evans (1961).
Since then the computation of long spectra with powerful
computers has become more popular than the
application of complex multistage algorithms.
2.2 Nonparametric dispersion estimation
The average of the local
LSS spectra gave the crude
frequency estimates during the first stage of the simple
multistage search described above.
Pelt (1983, 1997)
has introduced an alternative to compute these estimates.
The idea is that if the data form a continuous periodic curve,
the dispersion around this curve can be estimated without solving
the curve itself.
This dispersion is measured with the nonparametric test statistic
where
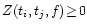 deviates from zero only if
deviates from zero only if
The
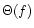 test statistic is a good approximation of
the
LSS(f) spectrum.
A spectral window can be introduced like in
the standard Fourier estimation.
This is achieved with the more general formulation
test statistic is a good approximation of
the
LSS(f) spectrum.
A spectral window can be introduced like in
the standard Fourier estimation.
This is achieved with the more general formulation
that allows additional smoothing with the data window
The value of
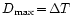 gives the maximum resolution for the
gives the maximum resolution for the 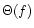 spectrum,
because
spectrum,
because
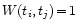 for all pairs of observations.
Adjusting this algorithm parameter to
for all pairs of observations.
Adjusting this algorithm parameter to
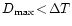 enables a faster computation of a smoother spectrum.
This reduces the number of tested frequencies during the
first stage of the analysis,
because a smaller
Dmax allows a longer step
enables a faster computation of a smoother spectrum.
This reduces the number of tested frequencies during the
first stage of the analysis,
because a smaller
Dmax allows a longer step
 in the tested frequencies.
in the tested frequencies.
Although 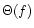 involves double summation for every tested frequency,
this apparently complex test statistic can be computed effectively
by rearranging these sums and using trigonometric approximations.
Such computational techniques for different realizations of the
algorithm can be found in (Pelt 1980, 1992).
The application of this method speeds up the complete multistage
analysis, because the
involves double summation for every tested frequency,
this apparently complex test statistic can be computed effectively
by rearranging these sums and using trigonometric approximations.
Such computational techniques for different realizations of the
algorithm can be found in (Pelt 1980, 1992).
The application of this method speeds up the complete multistage
analysis, because the 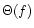 spectrum for a full grid of
tested frequencies can usually be computed as efficiently as
the fast Fourier transform.
spectrum for a full grid of
tested frequencies can usually be computed as efficiently as
the fast Fourier transform.
One particular version of a multistage analysis that can
also utilize the additional information of the measurement errors
is presented below.


Up: Three stage period analysis
Copyright The European Southern Observatory (ESO)
![]() in our period search.
The Q free parameters are
in our period search.
The Q free parameters are
![]() ,
,
![]() ,
...,
,
..., ![]() .
The most probable periodicity is searched for by determining
the absolute minimum for the sum of the squared residuals
.
The most probable periodicity is searched for by determining
the absolute minimum for the sum of the squared residuals
![$\displaystyle {\mathrm{RSS}} =
\sum_{i=1}^{n} \left[
y(t_{\mathrm{i}})-g(t_i,\beta_1,...,\beta_Q) \right]^2.$](/articles/aas/full/1999/18/ds1588/img45.gif)

![$\displaystyle {\mathrm{LSS}} (\beta_{R+1},\!...,\beta_Q)
\! \! = \! \! \! \sum_...
...a_1, \!...,\hat \beta_R,
\beta_{R+1},\!...,\beta_Q)
\! \right]^{\! 2} \!\!\!\!,$](/articles/aas/full/1999/18/ds1588/img50.gif)
![$\displaystyle g(f)\!=\!
\hat B_0(f) \! + \!
\sum_{r=1}^R \!
\left[
\hat B_r (f) \cos(r 2 \pi f t_i) \! + \!
\hat C_r(f) \sin(r 2 \pi f t_i) \!
\right]\! ,$](/articles/aas/full/1999/18/ds1588/img52.gif)
![$\displaystyle \Theta (f)={{\sum_{i=1,j=i+1}^{n-1,n}
Z(t_i,t_j,f)
\left[ y(t_i)-y(t_j) \right]^2} \over
{\sum_{i=1,j=i+1}^{n-1,n}
Z(t_i,t_j,f),}}$](/articles/aas/full/1999/18/ds1588/img75.gif)
![$\displaystyle \Theta(f)={{\sum_{i=1,j=i+1}^{n-1,n}
Z(t_i,t_j,f) W(t_i,t_j)
\lef...
..._i)-y(t_j) \right]^2} \over
{\sum_{i=1,j=i+1}^{n-1,n}
Z(t_i,t_j,f) W(t_i,t_j)}}$](/articles/aas/full/1999/18/ds1588/img79.gif)
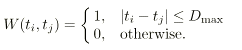
![]() involves double summation for every tested frequency,
this apparently complex test statistic can be computed effectively
by rearranging these sums and using trigonometric approximations.
Such computational techniques for different realizations of the
algorithm can be found in (Pelt 1980, 1992).
The application of this method speeds up the complete multistage
analysis, because the
involves double summation for every tested frequency,
this apparently complex test statistic can be computed effectively
by rearranging these sums and using trigonometric approximations.
Such computational techniques for different realizations of the
algorithm can be found in (Pelt 1980, 1992).
The application of this method speeds up the complete multistage
analysis, because the ![]() spectrum for a full grid of
tested frequencies can usually be computed as efficiently as
the fast Fourier transform.
spectrum for a full grid of
tested frequencies can usually be computed as efficiently as
the fast Fourier transform.