Before comparing the widths provided by the semi-clas-sical method and the
collision rate method (respectively hereafter referred to as SCM and
CRM), we must first determine the limits in density of the impact approximation,
that is the densities above which the impact approximation does not apply.
It is well known (Sobel'man et al. 1981) that the impact approximation is
valid for the level n if the dimensionless quantity ![]() is very small compared to unity. This
gives the "limiting'' values mentioned in Table 1 below.
is very small compared to unity. This
gives the "limiting'' values mentioned in Table 1 below.
Further, the density must be taken below the Inglis-Teller limit given in Griem (1974) by:
 |
||
| (32) |
The cut-offs on the impact parameters are:
| (33) |
![\begin{displaymath}
\rho _{\min }\approx \left( \frac 23\right) ^{1/2}\frac \hbar {mv_{\rm e}}\left[
G\left( n,\Delta n\right) \right] ^{1/2} \end{displaymath}](/articles/aas/full/1999/17/ds5435/img111.gif) |
(34) |
The other characteristic radii are:
Following the two approaches described in the previous sections, we have
calculated the electron impact linewidths of a few ![]() lines at densities
varying from 109 to 1017 cm-3 and T=104 K. The results are given
in Table 2 below.
lines at densities
varying from 109 to 1017 cm-3 and T=104 K. The results are given
in Table 2 below.
 |
Table 2 shows discrepancies between CRM and SCM at nearly all densities,
especially at low densities which correspond to large values of the Debye
radius. Analogous results are found for ![]() and
and ![]() transitions. Nevertheless, for
transitions. Nevertheless, for ![]() transitions, the interference
term in the electron collision operator
transitions, the interference
term in the electron collision operator ![]() is known to be less
significant, so that the CRM could provide satisfactory results for the
linewidths. Hence, the SCM with the chosen lower cut-off overestimates the
linewidths for
is known to be less
significant, so that the CRM could provide satisfactory results for the
linewidths. Hence, the SCM with the chosen lower cut-off overestimates the
linewidths for ![]() especially at low densities. Another cut-off
must be determined such as to obtain agreement with the CRM. This occurs when
especially at low densities. Another cut-off
must be determined such as to obtain agreement with the CRM. This occurs when ![]() is designated to be larger. This would be in agreement with the
validity of the SCM. Finally, the CRM described in this work remains an
alternative tool for determining linewidths at low electron densities.
is designated to be larger. This would be in agreement with the
validity of the SCM. Finally, the CRM described in this work remains an
alternative tool for determining linewidths at low electron densities.
Electron and ion impact widths are compared quantitatively in Table 3 for
![]() and
and ![]() cm-3.
cm-3.
![\begin{eqnarray}
\Delta \omega _i
&=&\frac 43\pi \left( \frac \hbar {m_{\rm e}}\...
...\rho _{\max }/\rho _{\min }+0.5\right]
F\left( n,\Delta n\right). \end{eqnarray}](/articles/aas/full/1999/17/ds5435/img123.gif) |
||
| (35) |
![\begin{displaymath}
\rho _{\min }=\left( \frac 23\right) ^{1/2}\frac \hbar {m_{\...
...gle
\frac 1{v}\right\rangle [F\left( n,\Delta n\right) ]^{1/2} \end{displaymath}](/articles/aas/full/1999/17/ds5435/img124.gif) |
(36) |
![\begin{eqnarray}
v=\left[ 2kT\pi /\mu \right] ^{1/2} & = & \left[ 2kT\pi /\left(...
...) \right]
^{1/2}\nonumber \\ & = & 2\left[ kT\pi /M\right] ^{1/2} \end{eqnarray}](/articles/aas/full/1999/17/ds5435/img125.gif) |
||
| (37) |
 |
(38) |
![\begin{eqnarray}
\Delta \omega _i = \frac 43\pi \left( \frac \hbar {m_{\rm e}}\r...
...ft[ \ln C+0.5\right]\nonumber \\ \times F\left( n,\Delta n\right)\end{eqnarray}](/articles/aas/full/1999/17/ds5435/img127.gif) |
||
| (39) |
 |
(40) |
![\begin{eqnarray}
\Delta \omega _i=3.487~10^{-4}T^{-1/2}N_i\left[ \ln C+0.5\right]\nonumber \\ \times F\left( n,\Delta n\right) \end{eqnarray}](/articles/aas/full/1999/17/ds5435/img129.gif) |
||
| (41) |
The Table 3 shows a domination of ion contribution to impact broadening of
![]()
![]() and
and ![]() lines for all the atomic levels
concerned with this work. It is observed that electron broadening is
expected to take over for n>20, as claimed by Griem (1967).
lines for all the atomic levels
concerned with this work. It is observed that electron broadening is
expected to take over for n>20, as claimed by Griem (1967).
For electron densities above the impact approximation limit - for ions - and below the Inglis-Teller limit, the quasistatic approximation can be applied to ions, but the impact approximation still applies to electrons for n varying between 5 and 20.
In this case, theoreticians of lines broadening commonly define the profile of the line emitted during the transition from the level m to the level n, and broadened by electrons and ions, by:
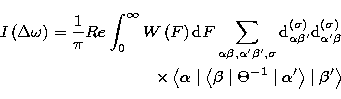 |
||
| (42) |
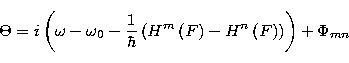 |
(43) |
Since ![]() is not diagonal in the parabolic representation, the
difficulty in this formulation lies in the inversion of large matrices.
For memory, the size of matrices to be inverted is
is not diagonal in the parabolic representation, the
difficulty in this formulation lies in the inversion of large matrices.
For memory, the size of matrices to be inverted is ![]() . Nevertheless,
we can simplify the problem by building from
. Nevertheless,
we can simplify the problem by building from ![]() and operator
and operator ![]() which would be diagonal in the
parabolic representation (see Seaton 1990). A diagonal operator can also
be obtained by simply neglecting the off-diagonal elements of
which would be diagonal in the
parabolic representation (see Seaton 1990). A diagonal operator can also
be obtained by simply neglecting the off-diagonal elements of ![]() According to Griem (1960) and Sobel'man (1963, 1972), an approximate profile
can be obtained by replacing
According to Griem (1960) and Sobel'man (1963, 1972), an approximate profile
can be obtained by replacing ![]() by half-width
by half-width ![]() of the
line i.e.:
of the
line i.e.:
 |
||
| (44) |
Copyright The European Southern Observatory (ESO)