Quantum calculations if they apply, provide good results, but they do not
constitute a rapid way to obtain the linewidths, especially for ion
broadening. On the other hand, it is known (Sobel'man et al. 1981) that for
highly excited states (![]() and
and ![]() , the electron impact widths can be expressed approximately in terms of the total
transition rates of the level n and
, the electron impact widths can be expressed approximately in terms of the total
transition rates of the level n and ![]()
For highly excited states, the electron-produced width can be approximated by:
| (21) |
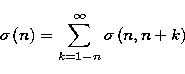 |
(22) |
In (21), the interference term is not taken into account. Its contribution,
which is more important for ![]() transitions is considered to be
cancelled by the adiabatic contribution, since the major contribution to
electron broadening comes from inelastic collisions. Thus, the summation in
Eq. (22) must be taken over
transitions is considered to be
cancelled by the adiabatic contribution, since the major contribution to
electron broadening comes from inelastic collisions. Thus, the summation in
Eq. (22) must be taken over ![]() .
.
Gee et al. (1976) have proposed a semi-empirical formula for the calculation
of e-- atom excitation cross section ![]() - de-excitation cross section being obtained via
the detailed balance equation - for electrons energies obeying:
- de-excitation cross section being obtained via
the detailed balance equation - for electrons energies obeying:
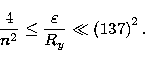 |
(23) |
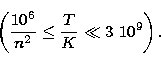 |
(24) |
In fact, putting ![]() where
where ![]() is the perturber's kinetic energy (here the electron), one easily
obtains:
is the perturber's kinetic energy (here the electron), one easily
obtains:
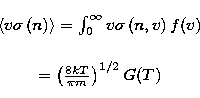 |
(25) |
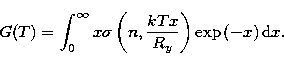 |
(26) |
There are three collision rate methods. The first (Method A) consists of determining total transition rates by summation of transition rates provided by the semi-em-pirical formula of Gee et al. (1976). The second (Method B) is based on the semi-empirical formula of Sobel'man et al. The third (Method C) is the numerical method developed in this work, which uses accurate transition cross sections available in the literature.
Using these methods, we have calculated the total transition rates for a few
hydrogen lines. The results obtained were compared in Motapon & Tran
Minh (1995). Good agreement was found between methods A and C using the
conditions of Gee et al.'s semi-empirical formula. A good agreement was also
found between methods B and C, except for high n (about 100) at high
energies (![]() K).
K).
In the atomic energy level range we are concerned with, elastic collisions
dominate ion broadening. Thus, the collision rate method for ions requires
cross sections for elastic scaterring. On the other hand, the
approximation of complete degeneracy yields divergent cross sections for
the process ![]() (Toshima 1977a,b); Pengelly &
Seaton (1964), so that this degeneracy must be removed by the fine structure
and the Lamb shift, the hyperfine structure being neglected here. The total
cross section
(Toshima 1977a,b); Pengelly &
Seaton (1964), so that this degeneracy must be removed by the fine structure
and the Lamb shift, the hyperfine structure being neglected here. The total
cross section ![]() is given by:
is given by:
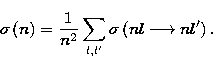 |
(27) |
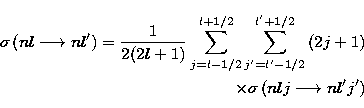 |
||
| (28) |
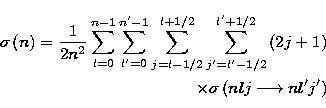 |
||
| (29) |
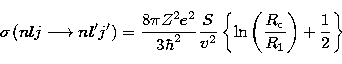 |
(30) |
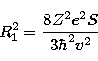 |
(31) |
where ![]() being a
dipole matrix element in the j-representation (Condon & Shortley 1959).
being a
dipole matrix element in the j-representation (Condon & Shortley 1959).
![]() is the energy splitting between
is the energy splitting between ![]() and
and ![]()
Transition rates can be carried out in a similar way as in the electronic case.
From a general point of view, estimations give ![]() to
be less than
to
be less than ![]() for the atomic levels involved in the transitions we
are interested in. On the other hand, in the ordinary conditions (
for the atomic levels involved in the transitions we
are interested in. On the other hand, in the ordinary conditions (![]() to 40000 K) the Debye radius
to 40000 K) the Debye radius ![]() (
(![]() in
centimetres) is greater than
in
centimetres) is greater than ![]() unless the density
exceeds 109 cm-3. Hence, the density range for application of the
collision rate method to ions is reduced since the impact approximation for
ions impose
unless the density
exceeds 109 cm-3. Hence, the density range for application of the
collision rate method to ions is reduced since the impact approximation for
ions impose ![]() cm-3. Furthermore, there is a formal analogy
between this description and the traditional semi-classical one. It finally
comes out that one can merely apply the formulae (5) to (8) of Hoang Binh et
al. (1987) to the calculation of
cm-3. Furthermore, there is a formal analogy
between this description and the traditional semi-classical one. It finally
comes out that one can merely apply the formulae (5) to (8) of Hoang Binh et
al. (1987) to the calculation of ![]() , especially because in
this density range, the semi-classical description (given above) does not
yet break down.
, especially because in
this density range, the semi-classical description (given above) does not
yet break down.
Copyright The European Southern Observatory (ESO)