3 A joint approach

As the maximum entropy procedure is a non-linear one, the separate approach is not optimum: because of the non-linearity, it is desirable to include all possible data during the deconvolution. That is, it is desirable to perform a joint deconvolution of all the Stokes parameters. In doing so, we can make sure of the positivity of the total intensity and that the fractional polarized intensity is less than 1. Furthermore, it is interesting to note that polarimetry can also provide constraints on large-scale structure of the total intensity: when the total intensity is very broad and smooth, and the polarized emission is varying on a much smaller scale size, it is possible for an interferometer to resolve out the total intensity and not the polarized emission. The result is instances where the emission is apparently more than 100% polarized. Such extreme cases certainly exist - see Wieringa et al. (1993) for excellent examples. In these cases, a joint algorithm will constrain the total intensity to be consistent with the polarized emission - i.e. more of the large-scale total intensity structure will be recovered.

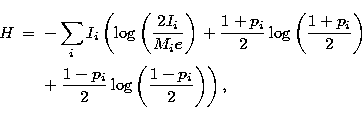
An undesirable aspect of a joint algorithm is that unmodelled errors in one image can be propagated into the other images. For example, it is common for thermal noise to be the limit to polarization images, whereas larger unmodelled systematic errors are the limit in total intensity. In this case, joint deconvolution can allow the larger errors in total intensity to couple through to the polarized images.

A measure of the joint entropy of a collection of Stokes images was first formulated by Ponsonby (1973), and elaborated by Gull & Skilling (1984) and Narayan & Nityananda (1986). Despite being well described for many years, it appears that the only previous application of this measure is by Holdaway & Wardle (1990) in analysing VLBI data. Following them, we use the entropy measure

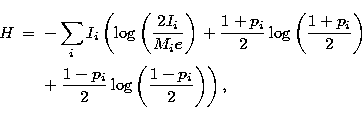$$\begin{eqnarray} H &=& - \sum_i I_i\left(\log \left(\frac{2I_i}{M_ie}\right)\rig... ... &&+\left. \frac{1-p_i}{2}\log\left(\frac{1-p_i}{2}\right)\right),\end{eqnarray}$$ (6)

where I_i and p_i are the total intensity and fractional polarization of the ith pixel respectively, and M_i is the default image (note here we use a different scaling to Holdaway & Wardle). In this entropy measure, the two terms containing the fractional polarization, p, will always contribute to reducing the total entropy, and the minimum reduction is achieved when p is zero. That is, the entropy measure tends to minimize the fractional polarization. In particular, in the absence of data constraints, the maximum entropy solution is I_i=M_i and p_i=0, and in the absence of polarization data, this measure reduces to the total intensity case, Eq. (3). This entropy measure naturally ensures that the total intensity must be positive and that the fractional polarized intensity must be less than 1.

Again following Holdaway & Wardle, we have formulated the deconvolution step as maximizing the objective function

$$\begin{eqnarray} J = H - \alpha\chi^2_{\rm I} - \beta\chi^2_{\rm P}.\end{eqnarray}$$ (7)

Here $\chi_{\rm I}^2$ and $\chi_{\rm P}^2$ are two data constraints, with Lagrange multiplies $\alpha$ and $\beta$, corresponding to one constraint each for total and polarized intensity mosaiced images. These are defined similarly to Eq. (2), except that $\chi_{\rm P}^2$ sums over all the polarized images. Single-dish $\chi^2$ constraints can be added in the same way.