

Up: Polarimetric imaging of large
The details of the maximum entropy solver that we have used is
derived from the algorithm
of
Cornwell & Evans (1985) with modifications
by
Sault (1990). It is based on a modified Newton-Raphson
iterative scheme: the algorithm proceeds by evaluating first- and
second-order derivatives of the objective function, and, from these,
deducing changes to make to the images and the
Lagrange multipliers. For reference, we give the derivatives of the entropy
measure for the joint approach in an appendix (this corrects some apparent errors in
Holdaway & Wardle 1990).
In computing these changes, the matrix of
second derivatives (the Hessian matrix) needs to be inverted. The size of
this matrix is  ,where
,where  is the number of pixels per image,
is the number of pixels per image, 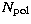 is the
number of polarizations (i.e. 1 for separate, and up to 4 for joint
deconvolution) and
is the
number of polarizations (i.e. 1 for separate, and up to 4 for joint
deconvolution) and 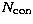 is the number of
Lagrange multipliers (i.e. 1, 2 or 3). To make this inversion feasible,
we follow Cornwell & Evans and approximate the
point-spread
function in the Hessian as a delta function. Additionally, in the joint
deconvolution, we ignore the mixed
second-order derivatives of H (i.e.
is the number of
Lagrange multipliers (i.e. 1, 2 or 3). To make this inversion feasible,
we follow Cornwell & Evans and approximate the
point-spread
function in the Hessian as a delta function. Additionally, in the joint
deconvolution, we ignore the mixed
second-order derivatives of H (i.e.
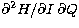 , etc.).
As with
Sault (1990), this makes the Hessian a sufficiently
simple form that inversion is straightforward and the changes can be determined.
, etc.).
As with
Sault (1990), this makes the Hessian a sufficiently
simple form that inversion is straightforward and the changes can be determined.


Up: Polarimetric imaging of large
Copyright The European Southern Observatory (ESO)