2 A separate approach

The mosaicing schemes that we have used follow the approach of Sault et al. (1996) in which the task of forming a final image is broken into two steps. First, dirty linearly mosaiced images of the relevant Stokes parameters are formed from the interferometric visibility data. Second, this dirty mosaiced image is `deconvolved' to form the final images. The simplest approach to deconvolving the different Stokes parameters is to deconvolve them separately (i.e. independently of each other). In this case, the use of the maximum entropy method is well established in mosaic deconvolution - see Cornwell (1988) and Sault et al. (1996) for descriptions. In particular, for a particular Stokes parameter, the maximum entropy process finds that solution image S which maximizes

$$\begin{eqnarray} J = H - \alpha\chi^2.\end{eqnarray}$$ (1)

Here H is the entropy measure of the solution image, $\chi^2$ gives a data constraint, and $\alpha$ is a Lagrange multiplier. Following Sault et al. (1996), we use

$$\begin{eqnarray} \chi^2 = \sum_i^{N_{\rm pix}} (D[S_i] - S_{{\rm D},i})^2/\sigma^2_i - N_{\rm pix}\end{eqnarray}$$ (2)

where S_i is the value of the ith pixel of the solution (here we use S to denote any Stokes parameter), $N_{\rm pix}$ is the number of pixels in the mosaiced image, $S_{\rm D}$ is the dirty linearly mosaiced image, and D is the linear operator which converts an estimate of S into a dirty mosaiced image (the operator D involves first, for each pointing, applying a primary beam and convolving with a dirty beam, and second performing a linear mosaicing operation).

This approach is readily augmented to include single-dish data by adding a second $\chi^2$ constraint (and second Lagrange multiplier). This constraint is similarly defined to Eq. (2), measuring squared difference between the single-dish image and the smoothed solution image.

The entropy measure most commonly advocated in deconvolution problems is

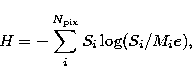$$\begin{eqnarray} H = -\sum_i^{N_{\rm pix}} S_i\log(S_i/M_ie),\end{eqnarray}$$ (3)

where M_i is the so-called "default image'' (in the absence of a data constraint, the maximum entropy solution is S_i=M_i). This measure is clearly inappropriate for polarized quantities as the pixel values, S_i, need to be positive. However, as Narayan & Nityananda (1986) pragmatically note, there are many functional forms which can produce good "entropy measures'' even if these have no basis in information theory. We have used a measure suggested by T.J. Cornwell (private communication), which has the form

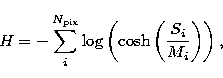$$\begin{eqnarray} H = -\sum_i^{N_{\rm pix}} \log\left(\cosh\left(\frac{S_i}{M_i}\right)\right),\end{eqnarray}$$ (4)

and which he has called the maximum emptiness criterion. In the absence of data constraints, the corresponding solution image is S_i=0. The rationale for this entropy measure is that, for $\vert S_i\vert \gg \vert M_i\vert$,

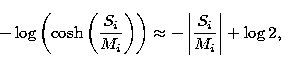$$\begin{eqnarray} -\log\left(\cosh\left(\frac{S_i}{M_i}\right)\right) \approx -\left\vert\frac{S_i}{M_i}\right\vert + \log2,\end{eqnarray}$$ (5)

and so by choosing M_i less than, or comparable to the noise level, maximizing H is approximately equivalent to minimizing the L₁-norm of the solution image. As is well known (e.g. Press et al. 1986), minimum L₁-norm solutions have the property of not giving undue weight to "outliers''. In our context, the measure will prefer a solution image which is mostly empty, but it will not give undue weight to attempting to eliminate some regions of significant emission (i.e. outliers from emptiness).