Effective collision strengths are calculated for transitions from the
ground 1s2 1S0 state to all fine-structure levels of the
excited states of 1s2![]() (
(![]() ) and 1s3
) and 1s3![]() (
(![]() )configurations. They are obtained for a temperature range
)configurations. They are obtained for a temperature range ![]() K.
This is the range of the largest fractional abundance of SXV, if
they
are in ionization equilibrium (Arnaud & Rothenflug [1985]).
The resulting effective collision
strengths are analytically fitted to the form
K.
This is the range of the largest fractional abundance of SXV, if
they
are in ionization equilibrium (Arnaud & Rothenflug [1985]).
The resulting effective collision
strengths are analytically fitted to the form
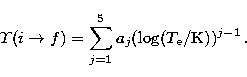 |
(7) |
![\begin{figure}
\includegraphics [width=6cm,clip]{H1380F1.PS}
\end{figure}](/articles/aas/full/1999/16/h1380/Timg40.gif) |
Figure 1:
Effective collision strengths of the |
![\begin{figure}
\includegraphics [width=6cm,clip]{H1380F2.PS}
\end{figure}](/articles/aas/full/1999/16/h1380/Timg42.gif) |
Figure 2:
Effective collision strengths of the |
![\begin{figure}
\includegraphics [width=6cm,clip]{H1380F3.PS}
\end{figure}](/articles/aas/full/1999/16/h1380/Timg47.gif) |
Figure 3:
Effective collision strengths of the
|
![\begin{figure}
\includegraphics [width=6cm,clip]{H1380F4.PS}
\end{figure}](/articles/aas/full/1999/16/h1380/Timg49.gif) |
Figure 4:
Effective collision strengths of the |
![\begin{figure}
\includegraphics [width=6cm,clip]{H1380F5.PS}
\end{figure}](/articles/aas/full/1999/16/h1380/Timg51.gif) |
Figure 5:
Effective collision strengths of the |
![\begin{figure}
\includegraphics [width=6cm,clip]{H1380F6.PS}
\end{figure}](/articles/aas/full/1999/16/h1380/Timg53.gif) |
Figure 6:
Effective collision strengths of the |
As mentioned in the Introduction two groups (Zhang & Sampson [1987];
Keenan et al. [1987]) reported effective
collision strengths for SXV. A comparison is made between the
present
result and the previous data. Figures 1 - 6 show
the comparison for the
excitation of the levels 1s2p 3P![]() and 1s3p 3P
and 1s3p 3P![]() with
J=0,1,2.
For other transitions the comparison is essentially the same as shown in
the previous paper
(Nakazaki et al. [1993]) and not repeated here. From the figures,
it is found that the values of Zhang &
Sampson ([1987]) are in good agreement with the
present ones. Zhang & Sampson ([1987]), however, reported their result only for the
excitation to n=2 levels. The result of Keenan et al. ([1987])
agrees with
that of the present calculation for all the transitions but the
excitations
to 1s3s 1S0 and 1s3p 3PJ (J=0,1,2) levels. The difference in the
latter transitions may be ascribed to an inadequate number of states
included in the R-matrix calculation which they used for their
interpolation.
All the R-matrix calculations include 11 lowest LS states,
while the present calculation takes into account 19 LS states.
Note that Keenan et al. ([1987]) reported no result for the excitation of the levels
of 1s3d configuration.
with
J=0,1,2.
For other transitions the comparison is essentially the same as shown in
the previous paper
(Nakazaki et al. [1993]) and not repeated here. From the figures,
it is found that the values of Zhang &
Sampson ([1987]) are in good agreement with the
present ones. Zhang & Sampson ([1987]), however, reported their result only for the
excitation to n=2 levels. The result of Keenan et al. ([1987])
agrees with
that of the present calculation for all the transitions but the
excitations
to 1s3s 1S0 and 1s3p 3PJ (J=0,1,2) levels. The difference in the
latter transitions may be ascribed to an inadequate number of states
included in the R-matrix calculation which they used for their
interpolation.
All the R-matrix calculations include 11 lowest LS states,
while the present calculation takes into account 19 LS states.
Note that Keenan et al. ([1987]) reported no result for the excitation of the levels
of 1s3d configuration.
In Fig. 3, we show a typical comparison between the present results and those of Dirac R-matrix calculation by Norrington et al. ([1998]). Figure 3 shows that the present result agrees very well with the fully-relativistic calculation except in the region of low temperature. Comparisons for other transitions (not shown here) have the same conclusion. This confirms the validity of the present method of the calculation of fine-structure transitions. In the region of low temperature, a small difference is seen between the two results. This may be ascribed to the difference in the resonance structure in the two sets of collision strength. Norrington et al. ([1998]) took account of only the states up to n=3. The present calculation includes the states with n=4. As for the resonance structure, therefore, the present calculation should be more accurate.
In conclusion the present paper presents the rate coefficients for
excitation from the ground 1s2 1S0 state to all the fine-structure
levels
of 1s2![]() (
(![]() ) and 1s3
) and 1s3![]() (
(![]() ) configurations of
SXV. In this sense the present calculation gives the most
comprehensive
data on the rate coefficients for the electron impact excitation of SXV.
The result may be of significance in application, e.g. to high
temperature
plasma in astronomy or laboratory.
) configurations of
SXV. In this sense the present calculation gives the most
comprehensive
data on the rate coefficients for the electron impact excitation of SXV.
The result may be of significance in application, e.g. to high
temperature
plasma in astronomy or laboratory.
Copyright The European Southern Observatory (ESO)