

Up: Rate coefficients for electron
Subsections
The nineteen lowest LS states of the target ion, i.e. 1s2 1S, 1s2s 1,3S, 1s2p 1,3P, 1s3s 1,3S,
1s3p 1,3P, 1s3d 1,3D, 1s4s 1,3S, 1s4p 1,3P, 1s4d
1,3D and
1s4f 1,3F, are included in the expansion of the wavefunction
in the R-matrix calculation.
Each state is represented by a configuration interaction wavefunction.
Ten basis orbitals 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f are used.
The radial part of the orbital
is expressed in the Slater form
|  |
(1) |
The coefficients Cj and the parameters pj and  for all the orbitals are
the same as those of Nakazaki et al. ([1993]). The excitation
energies were obtained from Hibbert's ([1975]) CIV3 program and
have been already presented by Nakazaki et al. ([1993]).
The resulting energies are in fair agreement with the experimental values determined
by Martin et al. ([1990])
and the oscillator strengths obtained
agree with those of other calculations
(Lin et al. [1977]; Drake [1979]).
Table 1 gives a list of the configurations included in our calculation.
for all the orbitals are
the same as those of Nakazaki et al. ([1993]). The excitation
energies were obtained from Hibbert's ([1975]) CIV3 program and
have been already presented by Nakazaki et al. ([1993]).
The resulting energies are in fair agreement with the experimental values determined
by Martin et al. ([1990])
and the oscillator strengths obtained
agree with those of other calculations
(Lin et al. [1977]; Drake [1979]).
Table 1 gives a list of the configurations included in our calculation.
Table 1:
Configurations mixed for each target symmetry
 |
The total wavefunction
representing the electron-ion collision system is expanded
in a sphere with radius  as follows:
as follows:
|  |
|
| (2) |
where  is the anti-symmetrization operator,
is the anti-symmetrization operator,  the channel
function representing the target state coupled with the spin and angular
functions for the scattered electron,
uij the continuum basis orbitals for the scattered electron,
and
the channel
function representing the target state coupled with the spin and angular
functions for the scattered electron,
uij the continuum basis orbitals for the scattered electron,
and  three-electron bound configurations formed from
the ten bound orbitals.
The coefficients cijk and djk
are determined by diagonalizing the total Hamiltonian of
the whole system with the basis set expansion defined by Eq. (2).
three-electron bound configurations formed from
the ten bound orbitals.
The coefficients cijk and djk
are determined by diagonalizing the total Hamiltonian of
the whole system with the basis set expansion defined by Eq. (2).
We use the computer code of Berrington et al. ([1995])
to calculate the
R-matrix on the boundary
of the sphere ( = 4.9 a.u.).
We include 39 continuum orbitals for each
angular momentum l to ensure
convergence in the energy range considered.
The calculations are made for all the partial waves with total angular
momentum L = 0 up to 14.
In the outer region of the sphere, a set of close-coupling equation
is solved using the asymptotic code STGFJJ
of Seaton. STGFJJ computes reactance matrices K
by matching the solutions in the inner and the outer regions at the
boundary
= 4.9 a.u.).
We include 39 continuum orbitals for each
angular momentum l to ensure
convergence in the energy range considered.
The calculations are made for all the partial waves with total angular
momentum L = 0 up to 14.
In the outer region of the sphere, a set of close-coupling equation
is solved using the asymptotic code STGFJJ
of Seaton. STGFJJ computes reactance matrices K
by matching the solutions in the inner and the outer regions at the
boundary
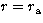 . The collision calculation is carried out over the energy
range
from the 1s2s 3S threshold to 480 Ryd.
The LS coupled K-matrices are transformed to
those for intermediate
coupling using the code JAJOM (Saraph [1978]), which yields
collision strengths between fine-structure levels.
The term-coupling coefficients are constructed from the unitary
matrices that diagonalize the non-relativistic Hamiltonian
and the Breit-Pauli Hamiltonian including the one-body mass-correction,
Darwin and spin-orbit terms.
Contributions from the partial waves higher
than
. The collision calculation is carried out over the energy
range
from the 1s2s 3S threshold to 480 Ryd.
The LS coupled K-matrices are transformed to
those for intermediate
coupling using the code JAJOM (Saraph [1978]), which yields
collision strengths between fine-structure levels.
The term-coupling coefficients are constructed from the unitary
matrices that diagonalize the non-relativistic Hamiltonian
and the Breit-Pauli Hamiltonian including the one-body mass-correction,
Darwin and spin-orbit terms.
Contributions from the partial waves higher
than 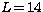 are
taken into account with
an extrapolation.
are
taken into account with
an extrapolation.
Rate coefficients for a transition from level i to level f
are defined as
|  |
(3) |
where gi is the statistical weight of the initial level  the
respective transition energy,
the
respective transition energy,
 the electron temperature, and k Boltzmann's constant.
Assuming a Maxwellian electron velocity distribution, the effective
collision strength
the electron temperature, and k Boltzmann's constant.
Assuming a Maxwellian electron velocity distribution, the effective
collision strength  is defined as
is defined as
|  |
(4) |
where 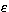 f is the energy of the electron after
the collision, and
f is the energy of the electron after
the collision, and 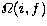 is the collision strength.
It should be noted that
is the collision strength.
It should be noted that  is symmetric over the transition
is symmetric over the transition
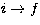 and
and  . To obtain the rate coefficient at high
temperature, we fit the present collision strengths in the non-resonance
region
to either of the following two analytic functions
. To obtain the rate coefficient at high
temperature, we fit the present collision strengths in the non-resonance
region
to either of the following two analytic functions
|  |
(5) |
and
|  |
(6) |
where X =  , where k2i is the
incident energy in Ryd and
, where k2i is the
incident energy in Ryd and 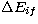 is given in Ryd.
For a dipole-allowed transition, the first one (5) is used with
D=0 and
E=4gifif/
is given in Ryd.
For a dipole-allowed transition, the first one (5) is used with
D=0 and
E=4gifif/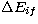 , where fif is
the oscillator strength for
, where fif is
the oscillator strength for 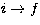 .The form (5) with E=0 is used for optically forbidden cases,
unless the
spin changes. For the spin-forbidden cases, the second one (6)
is employed.
The
parameters A, B, C, D, Fj (j=0-4) and
.The form (5) with E=0 is used for optically forbidden cases,
unless the
spin changes. For the spin-forbidden cases, the second one (6)
is employed.
The
parameters A, B, C, D, Fj (j=0-4) and  are determined by the least square method.
Thus the effective collision
strength is evaluated with the collision strengths calculated in the
resonance region and those fitted above that.
are determined by the least square method.
Thus the effective collision
strength is evaluated with the collision strengths calculated in the
resonance region and those fitted above that.


Up: Rate coefficients for electron
Copyright The European Southern Observatory (ESO)


![]() as follows:
as follows:

![]() = 4.9 a.u.).
We include 39 continuum orbitals for each
angular momentum l to ensure
convergence in the energy range considered.
The calculations are made for all the partial waves with total angular
momentum L = 0 up to 14.
In the outer region of the sphere, a set of close-coupling equation
is solved using the asymptotic code STGFJJ
of Seaton. STGFJJ computes reactance matrices K
by matching the solutions in the inner and the outer regions at the
boundary
= 4.9 a.u.).
We include 39 continuum orbitals for each
angular momentum l to ensure
convergence in the energy range considered.
The calculations are made for all the partial waves with total angular
momentum L = 0 up to 14.
In the outer region of the sphere, a set of close-coupling equation
is solved using the asymptotic code STGFJJ
of Seaton. STGFJJ computes reactance matrices K
by matching the solutions in the inner and the outer regions at the
boundary
![]() . The collision calculation is carried out over the energy
range
from the 1s2s 3S threshold to 480 Ryd.
The LS coupled K-matrices are transformed to
those for intermediate
coupling using the code JAJOM (Saraph [1978]), which yields
collision strengths between fine-structure levels.
The term-coupling coefficients are constructed from the unitary
matrices that diagonalize the non-relativistic Hamiltonian
and the Breit-Pauli Hamiltonian including the one-body mass-correction,
Darwin and spin-orbit terms.
Contributions from the partial waves higher
than
. The collision calculation is carried out over the energy
range
from the 1s2s 3S threshold to 480 Ryd.
The LS coupled K-matrices are transformed to
those for intermediate
coupling using the code JAJOM (Saraph [1978]), which yields
collision strengths between fine-structure levels.
The term-coupling coefficients are constructed from the unitary
matrices that diagonalize the non-relativistic Hamiltonian
and the Breit-Pauli Hamiltonian including the one-body mass-correction,
Darwin and spin-orbit terms.
Contributions from the partial waves higher
than ![]() are
taken into account with
an extrapolation.
are
taken into account with
an extrapolation.


