2 Photometric solutions

Although YY CMi exhibits well defined eclipses, the analysis of its light curves is quite difficult because:

a) the light curves show significant anomalies, and

b) the spectroscopic mass-ratio is not known.

The asymmetries in the light curves are pronounced around the two maxima. The O'Connell effect amounts to $\Delta m= {\rm Max~I} - {\rm Max~II}=0.025$, 0.030 and 0.025 in U, B and V bands, respectively. Light curve asymmetries can be explained by sunspot-like dark spots on the components [5, (Binnendijk 1960]; [8, Hilditch 1981]; [10, Linnell 1982)]. [15, Mullan (1975)] and several investigators felt the need to place spots on contact binaries to obtain better light curve solutions (e.g. [24, Van Hamme & Wilson 1985]; [12, Milone et al. 1987]; [16, Niarchos et al. 1992, 1994, 1998)]. Moreover, strong magnetic activity on late-type stars, and the existence of large spots on the surfaces of these stars are suggested by the high angular momentum loss in very close and contact binaries [25, (van't Veer & Maceroni 1988, 1989]; [11, Maceroni et al. 1990)]. Hence, the light curve anomalies in YY CMi can be tackled by invoking cool and/or hot spots on the components since YY CMi exhibits light curve anomalies in all the three bands. The lack of a spectroscopic mass ratio does not affect the photometric solution, although it makes it more difficult. The photometric solution was carried out by us in the following way.

2.1 Unspotted solution

First, we tried to solve the U, B and V light curves (individual points) of [1, Abhyankar (1962a)] without any spots on the two components using the [28, Wilson & Devinney (W-D) (1971)] method according to their improved version of 1993. For initiating the W-D programme, we used the values of a few of the required parameters given by [7, Giuiricin & Mardirossian (1981)], as initial parameters. We treated the following parameters as fixed: the temparature, $T_{\rm e,h}$ (6400 K) of the hot component (cf. 6360 K used by [18, Niarchos et al. (1998)] by assuming a spectral type of F6); the mass-ratio, q (0.8) of the system; the ratio of the surface rotation rates to synchronous rotation rates, $F_{\rm h}$ and $F_{\rm c}$ as unity; the limb darkening coefficients, $x_{\rm h}$ and $x_{\rm c}$; the albedos, $A_{\rm h}$ and $A_{\rm c}$; and the gravity darkening coefficients, $g_{\rm h}$ and $g_{\rm c}$ of the hotter and cooler components, respectively. According to the principles of the W-D method [13, (Milone et al. 1995)], we adjusted the following parameters; the inclination, i: the temperature of the cool component, $T_{\rm e,c}$; the surface potential of the hotter star $\Omega_{\rm h}$; the relative monochromatic luminosity of the hot component, $L_{\rm h}$ and the third light l₃. Sufficient number of runs of the DC programme was made until the sum of the residuals, $\Sigma W({\rm O}-{\rm C})^2$ showed a minimum and the corrections to the parameters became smaller than their probable errors. In order to check the internal consistency of the results [21, (Popper 1984)], separate solutions, for each of the U, B and V light curves, were made. The study of [2, Abhyankar (1962b)] suggested YY CMi to be a semi-detached system while [7, Giuricin & Mardirossian (1981)] and [18, Niarchos et al. (1998)] indicated it to be a contact binary. Hence, to ascertain the nature of the system, we analysed the light curves using W-D method with two different modes viz; mode-4 (semi-detached with primary filling the Roche lobe) and mode-3 (contact). The analysis with mode-4 (semi-detached with primary filling the Roche lobe) did not yield convergency, while the analysis with mode-3 (contact) yielded converged solutions and hence we proceeded with the contact nature of the system only. The results of the analysis, with mode-3, of individual U, B and V light curves indicated that the individual solutions are consistent and that a combined solution for U, B and V is adequate to derive the system parameters. Further, the fit of these results to the observations were found to be good except for the reduced light in the phase interval from 0.6 to 0.93.

Using the derived luminosities, the magnitude and colour of the comparison star [V=8.68, B=8.73 and U=8.84] and the corresponding differential magnitudes for unit luminosity at the quadrature [V=+0.320, B=-0.005 and U=-0.130], we derived the colours (B-V) and (U-B) of the primary, hot component to be 0.32 and -0.06.

Assuming no space reddening, the derived colours for the primary component corresponds to an average temperature of $7000 \, \pm \, 100$ K [3, (Allen 1976]; [20, Popper 1980]; [23, Schmidt-Kaler 1982)]. Hence, a reanalysis of the individual light curves as well as a combined solutions for U, B and V colours was made with $T_{\rm e,h}=7000$ K and various values of q (0.7 to 1.0) as fixed parameters. In this analysis the discordant points in the phase range 0.6 to 0.93 were removed from consideration. From a plot of the resulting $\Sigma W({\rm O}-{\rm C})^2$ against q it was found that the minimum occurs at q=0.90. The individual solution with q=0.90 are given in Cols. 2, 3 and 4 of Table 1.

  

Table 1: YY CMi: Elements obtained from the solution of individual and combined VBU light curves using W-D method

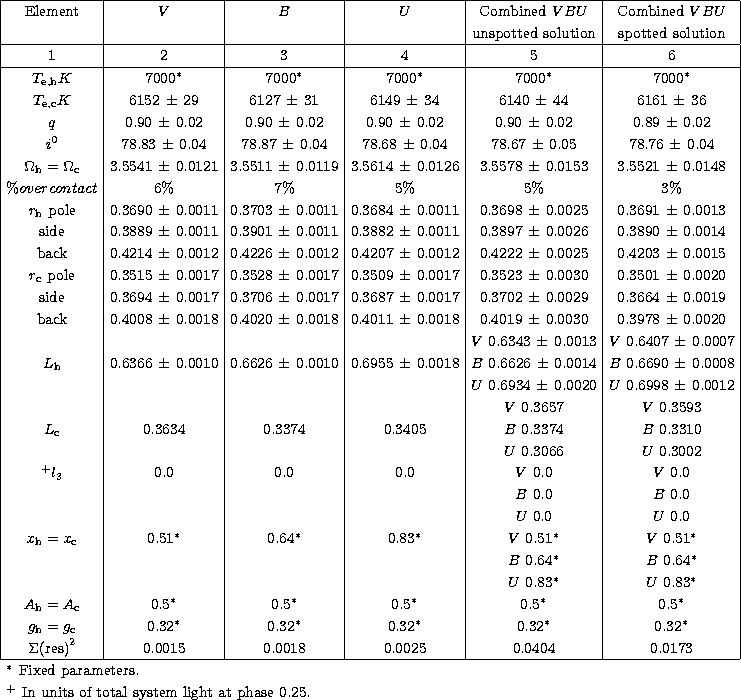Taking the average parameters of these solutions as preliminary elements a final combined solution was obtained keeping i, $T_{\rm h}$, $\Omega_{\rm h}$ and $L_{\rm h}$ as adjustable parameters and $x_{\rm h}$, $x_{\rm c}$, $g_{\rm h}$, $g_{\rm c}$,$A_{\rm h}$ and $A_{\rm c}$ as fixed parameters. It is given in Col. 5 of Table 1. One can notice that l₃ is absent in all the three colours in the individual as well as in the combined solutions. The theoretical curves obtained from the elements given in Table 1, Col. 5 are shown in Figs. 1a and 1b as solid lines.

  

Figure 1: a) YY CMi: Light curves in V and B passbands. Open diamonds represent V observations, open triangles represent B observations, solid lines represent unspotted solution and dashed lines represent spotted solution. b) YY CMi: Light curve for the U passband. Open squares represent U observations, solid line represents unspotted solution and dashed line represents spotted solution

In these figures, the open diamonds (V), open triangles (B) and open squares (U) represent the individual observations of [1, Abhyankar (1962a)].

2.2 Spotted solution

Figures 1a and 1b do show that the theoretical light curves of the unspotted solutions fit the data quite well except the reduced light in the phase range 0.6 to 0.93. So we tried to obtain a better fit by introducing a cool spot on the surface of the secondary (cooler) component. The spot region was centered in the co-latitude ranges 90 to 60 degrees, while the other spot parameters namely longitude (measured counter-clockwise on the secondary as defined in the Wilson-Devinney programme), angular size and temperature factor were first selected by trial and error to reproduce the light curve perturbations by using the parameters found in the unspotted solution in the LC (light curve) programme of the Wilson & Devinney. The spot parameters were later subjected to a DC programme which gave the results listed in Table 2.

  

Table 2: YY CMi: Comparison of the spot parameters obtained from the present studies and by [18, Niarchos et al. (1998)] on the secondary component

$\parbox{16cm}{ $^*$\space Fixed parameter.\\ $^{**}$\space T.F is the... ...d in the W-D programme (see text). The system is assumed to revolve clockwise.}$

These data were used for deriving the spotted solution of the light curve. The temperature of the hotter (primary) component was fixed at the value found in the unspotted solutions. The other parameters namely, i, $T_{\rm c}$, $\Omega_{\rm h}$, q and $L_{\rm h}$ were varied. The differential corrections were calculated until the adjustments became smaller than their probable errors. The final results of the spotted solution is given in Table 1, Col. 6.

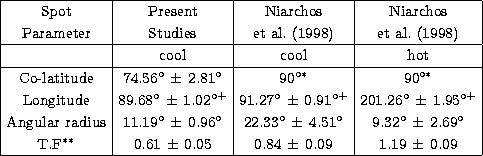
The theoretical light curves for the spotted solution are shown as dashed lines in Figs. 1a and 1b.

2.3 Comparison with the solution of
[18, Niarchos et al. (1998)]

First we note that we have derived $T_{\rm e,h}=7000$ K as compared to their $T_{\rm e,h}=6360$ K. But our value is preferred because it is based on UBV colours while theirs is based on V only. Similarly the fit of the spotted solution indicates that we do not need a hot spot on the secondary as found by [18, Niarchos et al. (1998)]. The parameters, except for the longitude, of the cool spot are also different from theirs. This indicates a variation in the spot activity on the secondary star of the binary.

The difference in the longitude of the cool spot in the two solutions can be simply explained by the fact that the revolution of the binary is defined in a different way in the two solutions. In [18, Niarchos et al. (1998)] the system revolves counter-clockwise (according to Binary Maker 2.0), while in our solution the revolution is assumed to be clockwise. In both solutions the cool spot is better seen at phase 0.75, thus explaining the deficiency of light around Max II.