4 Astrometric calibration

4.1 $\rho$ and $\theta$ calibration

Several wide double stars for calibration of differential astrometry parameters $\rho$ and $\theta$ were initially selected from the list of [2, Brosche & Sinachopoulos (1988)]. In the pre-Hipparcos era this source was believed to be a comprehensive and reliable compilation of visual binary star parameters. At the time of the present study the Hipparcos data [5, (ESA 1997)] became available for some of them. Only two of five pair-calibrators have independent observations of both components in the output catalogue: WDS 09233+0330 = HIP 46028/9 and WDS 12151+0959 = HIP 59739/7. Their parameters agree with Hipparcos rather satisfactory: differences in separation are 0$.\!\!^{\prime\prime}$03 and $-0\hbox{$.\!\!^{\prime\prime}$}06$ and in $\theta$ are $0.28\hbox{$^\circ$}$ and $0.18\hbox{$^\circ$}$, respectively.

  

Table 4: Astrometric standards' parameters. Reference column: "HIP" = [5, (ESA 1997)], "CDS" = [2, (Brosche & Sinachopoulos 1988)]

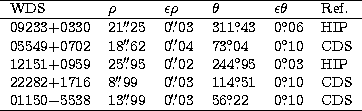The resulting data on our calibrators are shown in Table 4 with the reference to the source finally used.

Averaging of results gave a scale factor of our optical system $S=0.4456\pm0.0005$ ($^{\prime\prime}$/pixel) (see below Sect. 4.3). The correction for differential refraction which affects usually the measurements of wide double stars did not introduce significant change in the calibration. The moderate variations of ambient temperature also prevented a substantial scale drift.

The epochs of Hipparcos, the CDS list of [2, Brosche & Sinachopoulos (1988)] and our average epoch of observations are almost the same, so we needed no corrections for precession or relative proper motion of the components for position angle calibration. The astrometric standard position measurements provided the zero point of the position angle with relatively large uncertainty: $\alpha_{\theta}=\theta_{0}-\theta=89\hbox{$.\!\!^\circ$}88\pm0\hbox{$.\!\!^\circ$}16$.

Such a low quality of astrometric calibration data is supposedly related to the very short exposures taken. Indeed, the calibrators were bright objects and were observed in the V -band, so the duration of exposures was about 3 s. It is well known (e.g. [9, Lindegren 1980)] that it is not possible to achieve good and reproducible astrometric results with such exposures.

We also applied the trail technique for the determination of right ascension direction. Through the observational sets the stellar trails were taken in the V -band in total nine times, at least once in a mission. The time of passage of an equatorial star across the field of view was $\approx 10$ s. Two illustrative cases of these trails and their linear regression are shown in Fig. 1. It is clear that for trails as well as for astrometric standards a much longer exposure time should be used to get a more accurate calibration.

Evidently, low-frequency modulation of the atmospheric refractive index of line-of-sight air does not allow for a high-accuracy calibration of the position angle with such short exposures. The formal averaging of our 9 values for the inclination of the trail gave a $\theta$ zero point of $89\hbox{$.\!\!^\circ$}80\pm0\hbox{$.\!\!^\circ$}20$.This does not differ from the value obtained from the astrometric standard stars reduction. Therefore, as a final value we adopted $\alpha_{\theta}=89\hbox{$.\!\!^\circ$}84\pm0\hbox{$.\!\!^\circ$}1$.

4.2 Account for a differential chromatic refraction

We consider here the effect that the different colours of stars result in not equal shifts of their apparent positions. For this differential chromatic refraction (DCR) the separation between the components plays no role, but the spectral difference does (e.g. [10, Pravdo & Shaklan 1996)]. The reason is the atmospheric dispersion (while for differential monochromatic refraction it is the increasing of the refraction angle with zenith distance between two stars). Hence, even if we deal with relatively close binaries, we should investigate the significance of the DCR effect.

To check the importance of this effect in our case we calculated its approximate value for all the objects in the following way. First, we computed effective wavelengths in the U B V system for all the classes of stars. The spectral energy distributions $S(\lambda)$ [, (Straizys & Sviderskiene 1977)] were taken from A. Mironov (Sternberg Institute), who kindly supplied us with ready-to-use electronic tables. Then we computed the effective wavelengths $\lambda_{\rm eff}$ of stars in U , B  and V   bands according to the conventional formula (see, for example, [13, Straizys 1977], p. 16). Afterwards, given the known dependence of the refractive coefficient of air $N_{\rm air}(\lambda)$ [, (Allen 1977)], we computed for each observed star the value of the DCR effect and the apparent displacement of a secondary component relative to a primary. For this we assumed the stars to belong to the Main Sequence (MS) of the $\rm H-R$ diagram.

The most significant effect, up to 50 milliarcsec (mas) was found in the B -filter; in U and V it was only up to 10 mas; 10% of values exceed 20, 9 and 6 mas in B , U and V , respectively. Fortunately, in the B band there is no large difference in $\lambda_{\rm eff}$ between giant and dwarf stars and the treatment of all the stars as the MS ones does not introduce a large error.

Although the values are relatively small, we applied these corrections to our measurements. The resulting astrometric parameters are given in Table 3. One line per object is given representing the WDS designation and the HIP-number (when available), $\rho$ and $\theta$with errors and the number of observations. In this table we already averaged the results in different filters; the errors are assigned to the least error among the individual filter values (in most cases -- the values in U -filter, which was exposed longer). These final errors of the parameters include those of scale factor and $\theta$ zero point. The average uncertainty of our separations $\epsilon_{\rho}$ is less than 10 mas.

4.3 Comparison with Hipparcos

  The Hipparcos catalogue provides in the Double and Multiple Stars Annex (DMSA) the information for resolved binaries that is known to have quite a good precision. We compare the $\rho$ and $\theta$ from Hipparcos with our values where it is possible. The cross-identification of our sample of double stars with the Hipparcos stars was performed on the basis of coordinates comparison. The resulting list of common pairs contains 36 objects (see Table 3, Col. 2); all of them belong to part C of the DMSA (component solutions) and have solution quality A.

First, we find that our position angles differ from the Hipparcos ones by $+0\hbox{$.\!\!^\circ$}09$ on average, with a rms difference of 0$.\!\!^\circ$16. Thus we can conclude that the two sets of $\theta$ values practically do not differ.

Second, the average ratio of Hipparcos separations to ours

$$\left<\rho_{\rm HIP}/\rho\right\gt = 1.0020 \pm 0.0002.$$

The difference of this value from unity is significant. But taking this factor into account, the derived rescaled $\rho$ in our sample have standard deviation of only 7 mas from the Hipparcos ones, slightly more than the average Hipparcos error of separations for a given sample ($\left<\epsilon_{\rho}^{\rm HIP}\!\right\gt=5.1$ mas).