3 Photometric reduction

One basic assumption to obtain the absolute photometry data was that the extinction at cerro Las Campanas is the same as that measured at the Swiss telescope at cerro La Silla (which lies only 30 km to the south). In order to check this we obtained Bouguer curves for an E3-area standard star HD 49789 [6, (Graham 1982)] in the night of 30.11/1.12.91. Resulting extinction coefficients were quite close to the values that Genevian data for that night supply:

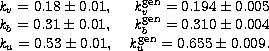
One can thus see that there is no significant difference neither in V nor in B filters. The lower extinction in our U filter is interpreted as caused by the slightly "redder" effective wavelength of our filter compared to the Genevian one. Hence, it was decided to apply Genevian values in B and V bands and 80% of ${\it k}_{\it u}^{\rm gen}$value for the extinction correction. The second-order extinction was neglected for two reasons. First, the colours $({\it B}-{\it V})$ of our objects are normally close to zero (76% of the components have $({\it B}-{\it V})<0.3$) and airmass was low (<1.5), so the expected error in ${\it k}_{\it b}$, ${\it k}_{\it u}$ was estimated not to exceed 0$.\!\!^{\rm m}$005. Second, to account properly for secondary extinction for early-type stars their two-dimensional spectral types have to be known (see [, Straizys 1972], p. 128).

From 13 photometric standard star measurements we determined the coefficients C and A of linear transformation from the instrumental to the standard U B V system: $M^{\rm std}-M^{\rm inst}=C_M+A_M \times CI^{\rm inst}$(here the colour index CI is $({\it B}-{\it V})$ for $M\equiv{\it V}$,$({\it B}-{\it V})$ and $({\it U}-{\it B})$ for $M\equiv({\it U}-{\it B})$). For our standards we used the data of [8, Landolt (1973)]; [6, Graham (1982)] and the improved photometric values kindly provided by [7, Grenon (1992)]. The derived colour dependency coefficients are: $A_V=0.122\pm0.005$, $A_{B-V}= 0.007\pm0.004$ and $A_{U-B}=0.077\pm0.014$.

The comparison of the photometric results obtained in different nights allowed us to determine the overall measure of photometry data reliability:

• Absolute photometry standard deviations:
  in V : $0.04^{\rm m}$, in $({\it U}-{\it B})$ and $({\it B}-{\it V})$ : $0.02^{\rm m}$;
• Differential photometry standard deviations:
  in $\Delta {\it V}$: $0.023^{\rm m}$, in $\Delta ({\it U}-{\it B})$ and $\Delta ({\it B}-{\it V})$: $0.015^{\rm m}$.

  

Figure 1: Two cases of stellar trails and their regression. These trails were taken in the same night but gave quite different apparent inclinations: $-0\hbox{$.\!\!^\circ$}13$ and $+0\hbox{$.\!\!^\circ$}06$

The final photometric results are given in Table 1. This table provides two lines per object, for primary component (A) and for secondary (B). As a primary identifier we choose the IDS-style designation formed from the coordinates for epoch 2000 taken from WDS (1996). The columns give this WDS and Durchmusterung designations of the star, component designation, V , $({\it U}-{\it B})$ and $({\it B}-{\it V})$ values with their errors, number of observations $N_{\rm obs}$ and a note sign. The notes are collected separately in Table 2. The errors were estimated from the individual spread of values in each observation and differences of values obtained in two nights. They do not include transformation errors, which were discussed above, and extinction uncertainties. It should be stressed that as photometry error for the secondaries we give those of differences of their V and colours with primaries. But, since the primary magnitudes were obtained from the total object magnitude $\rm Mag_{A+B}$ and magnitude difference $\Delta\ {\rm Mag}$ values, the errors for the A-component include both errors $\epsilon\ {\rm Mag}_{\rm A+B}$ and $\epsilon \Delta\ {\rm Mag}$.