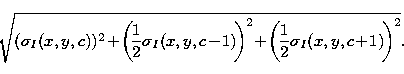Up: Faint source detection in
Subsections
As glitches are the main limitations for faint ISOCAM source detection,
not the noise, it is clear that an analysis on the
final raster image with a standard method (detection at  the
noise level + background) would lead to poor results if the glitches
with transients have not been removed. In order to avoid other
problems (dark current subtraction, flat field, transient and long drift
correction, etc.), a solution is to
perform a temporal source detection technique
rather than a standard source detection technique on the
final raster map. The temporal source detection method is based on the
fact that the flux observed by a single detector increases
when the detector points toward a source and decreases when the camera is moved
to the subsequent phase of a raster observation. This temporal
behavior of the flux observed by a detector has the advantage of being
dark current and flat field independent. Indeed, the flat field and dark
current act as a
multiplicative and an additive constant on the total temporal signal,
and do not effect the shape of the signal. Thus, the signature of a
source can be identified.
the
noise level + background) would lead to poor results if the glitches
with transients have not been removed. In order to avoid other
problems (dark current subtraction, flat field, transient and long drift
correction, etc.), a solution is to
perform a temporal source detection technique
rather than a standard source detection technique on the
final raster map. The temporal source detection method is based on the
fact that the flux observed by a single detector increases
when the detector points toward a source and decreases when the camera is moved
to the subsequent phase of a raster observation. This temporal
behavior of the flux observed by a detector has the advantage of being
dark current and flat field independent. Indeed, the flat field and dark
current act as a
multiplicative and an additive constant on the total temporal signal,
and do not effect the shape of the signal. Thus, the signature of a
source can be identified.
Short glitches (i.e. first type) can be easily removed by masking the position where
they appear (Starck et al. 1999). For each pixel (x,y), we
indicate the deglitched data as D(x,y,c,r) and the corresponding
mask as M(x,y,c,r) (0 if the position is masked, 1 otherwise), where
c and r indicate respectively the configuration (raster position)
and the readout number in this configuration.
Values corresponding to the same sky position and the same configuration
are averaged:
| 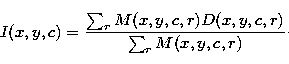 |
(12) |
The temporal noise 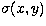 is estimated for each pixel
independently using a k-sigma clipping method, so the noise on the
mean value of signal in a configuration is given by:
is estimated for each pixel
independently using a k-sigma clipping method, so the noise on the
mean value of signal in a configuration is given by:
| 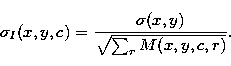 |
(13) |
The detection is done by calculating the signal:
|  |
(14) |
and its associated noise:

| 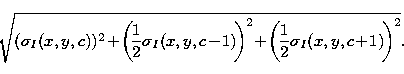 |
(15) |
Then we consider we have a detection at pixel (x,y) and at the
configuration c if:
| 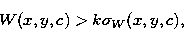 |
(16) |
where, in general, k is taken equal to 3. If a source is detected
at position (x,y,c) we put I(x,y,c)=1, otherwise I(x,y,c)=0. We
can therefore coadd the C I(x,y,c) matrixes in order to obtain a
matrix of detections with size equal to that of the total image:
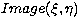 indicates how many times a source has been
detected at the sky position
indicates how many times a source has been
detected at the sky position  during the raster
observation. For instance, for a raster observation with half
overlapping,
during the raster
observation. For instance, for a raster observation with half
overlapping, 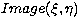 can take the integer values between 0
and 4.
can take the integer values between 0
and 4.
The detection has been made under the assumption of Gaussian noise. Due
the large number of glitches, false detections will occur. Two parameters
can be adjusted in
order to limit the number of false detections:
- 1.
- the detection level (k parameter). By default, the detection is done
at
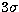 (it corresponds to a false detection probability of 0.25%).
Increasing the detection level eliminates false detections
(but also weaker objects).
(it corresponds to a false detection probability of 0.25%).
Increasing the detection level eliminates false detections
(but also weaker objects).
- 2.
- the number of required redundancy
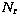 . For a raster made
by overlaping half the array, a source should be detected four times (two times if it
is on the border of the raster image). Fixing a minimum of two detections
should suppress most of the false detections.
. For a raster made
by overlaping half the array, a source should be detected four times (two times if it
is on the border of the raster image). Fixing a minimum of two detections
should suppress most of the false detections.
A robust detection is performed by comparing Image(x,y) to the number 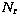 of
required redundancy. A high redundancy allows one to increase
of
required redundancy. A high redundancy allows one to increase 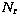 and improve
the robustness of the detection.
We point out that Image(x,y) is independent of the background level, the flat
field, and the dark.
and improve
the robustness of the detection.
We point out that Image(x,y) is independent of the background level, the flat
field, and the dark.
Once (Goldschmidt et al. 1997; Serjeant et al.
1997) the detection is done, sources must be extracted with
astrometric and photometric information. This is done using the final
calibrated raster image (see Siebenmorgen et al. 1996, for a complete
description of each calibration step). For observations with the six
arc second lens, the PSF is mainly contained in one single pixel. So
PSF fitting does not help, and the flux of an object can be obtained
by integrating the flux in a small box around the detected
position,using an estimate of the background. The gain
variation due to dippers and faders will have an effect on the accuracy
of the photometry, because it modifies the background on a
individual pixel. To summarize this approach, the advantages are that the
detection is relatively robust and independent of the dark current and the
flat field, while the drawbacks are:
- 1.
- the photometry is poor;
- 2.
- the temporal detection does not allow the use of correlation
between adjacent pixels, which is needed for extended weak sources
detection;
- 3.
- data cannot be coadded before detection.
To overcome these problems, the only way is to correct the data from
the gain variation due to faders and dippers.


Up: Faint source detection in
Copyright The European Southern Observatory (ESO)
![]() the
noise level + background) would lead to poor results if the glitches
with transients have not been removed. In order to avoid other
problems (dark current subtraction, flat field, transient and long drift
correction, etc.), a solution is to
perform a temporal source detection technique
rather than a standard source detection technique on the
final raster map. The temporal source detection method is based on the
fact that the flux observed by a single detector increases
when the detector points toward a source and decreases when the camera is moved
to the subsequent phase of a raster observation. This temporal
behavior of the flux observed by a detector has the advantage of being
dark current and flat field independent. Indeed, the flat field and dark
current act as a
multiplicative and an additive constant on the total temporal signal,
and do not effect the shape of the signal. Thus, the signature of a
source can be identified.
the
noise level + background) would lead to poor results if the glitches
with transients have not been removed. In order to avoid other
problems (dark current subtraction, flat field, transient and long drift
correction, etc.), a solution is to
perform a temporal source detection technique
rather than a standard source detection technique on the
final raster map. The temporal source detection method is based on the
fact that the flux observed by a single detector increases
when the detector points toward a source and decreases when the camera is moved
to the subsequent phase of a raster observation. This temporal
behavior of the flux observed by a detector has the advantage of being
dark current and flat field independent. Indeed, the flat field and dark
current act as a
multiplicative and an additive constant on the total temporal signal,
and do not effect the shape of the signal. Thus, the signature of a
source can be identified.
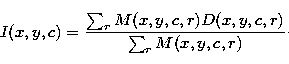
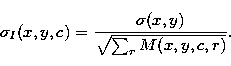

![]()