In a wavelet transform, a series of transformations of an image is generated, providing a resolution-related set of "views'' of the image. The properties satisfied by a wavelet transform, and in particular the à trous wavelet transform ("with holes'', so called because of the interlaced convolution used in successive levels: see step 2 of the algorithm below) are further discussed in (Starck et al. 1998).
We consider sampled data,
![]() , defined as the scalar product at
pixels k of the function f(x) with a scaling function
, defined as the scalar product at
pixels k of the function f(x) with a scaling function ![]() which corresponds to a low pass band filter:
which corresponds to a low pass band filter:
| (17) |
 |
(18) |
The smoothed data cj(k) at a given resolution j and at a position
k is the scalar product
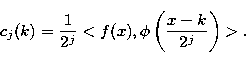 |
(19) |
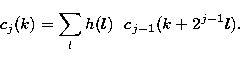 |
(20) |
| wj(k) = cj-1(k) - cj(k) | (21) |
 |
(22) |
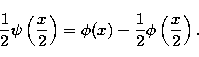 |
(23) |
A series expansion of the original signal, c0,
in terms of
the wavelet coefficients is now given as follows.
The final smoothed array ![]() is added to all the differences wj:
is added to all the differences wj:
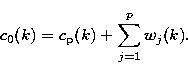 |
(24) |
At each scale j, we obtain a set ![]() . This has
the same number of pixels as the input signal.
. This has
the same number of pixels as the input signal.
The above à trous algorithm has been discussed in terms of a single
index, x, but is easily extendable to
two-dimensional space. The use of the B3 spline leads to a
convolution with a mask of ![]() :
:
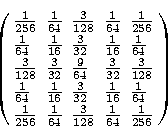 |
To facilitate computation, a simplification of this wavelet is to assume
separability in the 2-dimensional case. In the case of the B3 spline, this
leads to a row by row convolution with ![]() ; followed by column by column
convolution.
; followed by column by column
convolution.
As for the one dimensional case, an exact reconstruction is obtained
by adding all the scales and the final smoothed array:
 |
(25) |
We wish to thank Suzanne Madden for her kind help in the revision of the manuscript. We also would like to thank the anonymous referee whose comments had helped us to improve the quality of the paper.
Copyright The European Southern Observatory (ESO)