

Up: Faint source detection in
Subsections
In Fig. 1c, at readout 120,
a bump can be seen lasting one whole exposure time (30 readouts).
![\begin{figure}
\includegraphics [width=8.8cm,clip]{fig_3nglitch.ps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg3.gif) |
Figure 1:
These three plots show a single detector response in Analog to
Digital Units (ADU) as a function of time, expressed here in number of
readouts, where each readout corresponds to 2 s. Three types glitches
due to cosmic rays can be found here:
a) top: the most common glitches, lasting only one readout. b)
middle: a "fader'', occuring around readout 160. This glitch presents a slowly
decreasing tail. It has been truncated above 100 ADUs, but its original
intensity is 2558 ADUs. c) bottom: a "dipper'', beginning around readout
240. This glitch is followed by a memory effect lasting about 100 readouts.
In these observations, the camera draws a mosaic on the sky (raster). Hence as
long as an object, such as a star or a galaxy, is in the line of sight of
a given pixel, the measured signal increases. A faint galaxy is visible
on the bottom plot c) around readout 120, lasting only one position
in the raster. Dashed lines mark different observation positions |
This is the signal expected when the camera pointing is such that a
source falls on the examined pixel. Thus we see that temporal detection
of sources is a possible and useful alternative to the usual spatial
detection. This temporal
behavior of the observed flux by a pixel has the advantage of being
dark and flat independent. Indeed, the flat and dark act as a multiplicative
and an additive constant on the temporal signal, which does not affect
the shape of the signal.
The redundancy inside the raster can be used for robust detection.
For example, for a raster observation with successive array displacements
corresponding to one half of the array on the sky, a source
should be detected temporally four times (see Fig. 2).
![\begin{figure}
\begin{tabular}
{cc}
\includegraphics [width=7cm,clip]{fig_hdf_t...
...&
\includegraphics [width=7cm,clip]{fig_hdf_temp4.ps}
\end{tabular}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg4.gif) |
Figure 2:
Four pixel histories (top left pixel (4,12), top right pixel (12,12),
bottom left pixel (20,12), and bottom right pixel (27,12)). The signal in ADU is
plotted versus the readout number. The dotted lines indicate the change of camera
pointing (i.e. between two dotted lines, the observed flux is the same). The same
source is seen by the four pixels respectively at position 2,3,4,5. It can be
relatively easily detected in pixel (12,12) and (20,12), while it is more
difficult
to see it in pixels (4,12) and (27,12) |
A criterion for a robust
detection can be obtained by considering the number of times a source is
detected. In the case of Fig. 2, the source
can easily be detected by eye in the second and third plots while
in the other two, the signal is too noisy.
We tested an automatic "temporal detection technique'' which is
described in Appendix A.
Although its results are relatively robust, the technique still suffers
from severe limitations:
- 1.
- low signal to noise ratio (SNR): in a mosaic, a source
generally extends over several pixels. Co-adding them allows us to
increase the SNR. This is not possible in this technique.
- 2.
- poor photometry: because of the previous point and also
due to the difficulty of estimating the background level.
- 3.
- sources are split: the signal of weak sources extended
over several pixels (either because they are intrinsically extended or
because of the Point Spread Function, PSF, or because of the camera
distortion) is split, resulting again in a decrease of the SNR of the source.
- 4.
- false detections: false detections are possible for
a redundancy of 10 or more, when searching for extremely faint
objects, due to the large number of cosmic ray impacts.
In order to avoid these difficulties, it is necessary to identify
the glitches
with memory effects (faders and dippers), and extract them from the
data, if possible without loosing the associated information.
Co-addition then becomes possible and a standard spatial source detection
algorithm can be used, keeping in mind that noise is not homogeneously
distributed on the map. This is exactly what PRETI allows us to do.
New methods based on wavelet transforms have recently been
developed for source extraction in an image (Bijaoui & Rué
1995), and successfully adapted for spectral analysis (Starck
et al. 1997). Using such an approach, a temporal signal can be
decomposed in its different components, selected from their frequency.
In terms of noise, in the temporal technique the noise standard deviation
is divided by  (where
(where 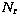 is the number of readouts
per raster position), while it is divided by
is the number of readouts
per raster position), while it is divided by
 (where
(where  is the number of
redundancies inside the raster, i.e. the number of pixels which see
the same sky position) for co-added data.
is the number of
redundancies inside the raster, i.e. the number of pixels which see
the same sky position) for co-added data.
In the Multi-Scale Vision Model (Bijaoui & Rué 1995), an object
in a signal is defined as a set of structures detected in the wavelet
space. The wavelet transform algorithm used for such a decomposition
is the so-called "à trous'' algorithm, which allows us to represent a
signal D(t) by a simple sum of its wavelet coefficients wj and a
smoothed version of the signal  (see Appendix B for more details
about the "à trous'' algorithm)
(see Appendix B for more details
about the "à trous'' algorithm)
| 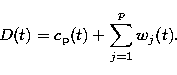 |
(1) |
The algorithm produces p+1 arrays of the same size, each one
containing only information
at a given frequency band. In such signals, we define a
"structure'' as a group of connected significant (above a given threshold)
wavelet coefficients. A complete description of how to estimate
the significance of a wavelet coefficient, which
depends on the nature of the noise, can be found in Starck et al.
(1998). An object is described as a hierarchical set of structures.
Two structures in a single object can be connected by "interscale-relation".
Consider two structures at two successive scales, S1j and
S2j+1.
Each structure is located on one of the individual arrays of the
decomposition and corresponds to a region where the
signal is significant. S1j is said to be connected to
S2j+1 if S2j+1 contains the pixel position
of the maximum wavelet coefficient value of S1j (i.e. the maximum
position of the structure S1j must also be contained in the structure
S2j+1). A set of connected structures is called an object in the
interscale connectivity graph.
Once an object is detected in wavelet space, it can be isolated by
searching for the simplest function which presents the same signal in
wavelet space. The problem of reconstruction (Bijaoui & Rué
1995) consists then in searching for a signal V such that its
wavelet coefficients are the same as those of the detected structure. By
noting  , the wavelet transform operator, and
, the wavelet transform operator, and  , the
projection operator in the subspace of the detected coefficients
(i.e.
, the
projection operator in the subspace of the detected coefficients
(i.e.  set all coefficients at scales and positions where
nothing was detected to zero), the solution can be found by minimizing the
following expression:
set all coefficients at scales and positions where
nothing was detected to zero), the solution can be found by minimizing the
following expression:
| 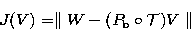 |
(2) |
where W represents the detected wavelet coefficients of the signal.
A complete description of algorithms for minimization of such a
functional can be found in (Bijaoui & Rué 1995).
In two dimensions, the method is identical.
Figure 3 shows how
several structures in different scales are linked together and form objects.
![\begin{figure}
\includegraphics [width=8.8cm]{8374f3.eps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg14.gif) |
Figure 3:
The Multiscale Vision Model: contiguous significant wavelet coefficients form
a structure, and following an interscale relation, a set of structures form an object.
Two structures Sj,Sj+1 at two successive scales belong to the same object if
the position pixel of the maximum wavelet coefficient value of Sj is included in
Sj+1 |
In ISOCAM data it is the cosmic ray glitches with memory effects
which are the typical
objects to be extracted from the time sequence of the
signal. Indeed, the signal associated with a fader or a
dipper type glitch is significant at several frequencies: a strong and rapid peak
makes them significant in the highest frequency wavelet coefficient
decomposition of the initial signal while the memory effect makes them
significant in the lower frequency wavelet coefficients. Hence, the
multi-scale approach is an ideal tool to discriminate glitches from
real signal. We will call pattern recognition, the action of
searching for objects showing properties typical of those expected for
faders and dippers.
The idea developed here is to use the multi-scale vision modeling for
a decomposition of a signal into its main components. In practice, a
simple object reconstruction from the detected structure in the
wavelet space, as proposed in Bijaoui & Rué (1995),
would produce poor results because of the strong confusion between the
numerous objects that can be found in the data. Moreover, wavelet
transforms present a drawback: the wings of the wavelet function are
negative (so that the integral of the function is zero) which implies that
when a positive signal falls onto one wing of the wavelet function it
produces a negative signal in the wavelet transform. The quality of
the object reconstruction is good only when additional constraints are
introduced, such as positivity constraint for positive objects, and negativity
constraint for negative objects. An object is defined as positive
(or negative) when the wavelet coefficient of the object,
which has the maximum absolute value, is positive (or negative).
The problem of confusion between numerous objects can be solved when
including a selection criterion in the detection of these
objects. Using the knowledge we have about the objects, in this case, glitches,
the problem of unknown object reconstruction is reduced to a pattern
recognition problem, where the pattern is the glitch itself. We only
search for objects which satisfy a given set of conditions in the
Multi-Scale Vision Model (MVM). For example, finding glitches of the
first type is equivalent to finding objects which are positive, strong,
and with a duration shorter than those of the sources. The method that
we use for the decomposition of the signal of a given ISOCAM pixel,
D(t0... tn), is summarized below:
- 1.
- detection of the glitches of the first type (i.e. few readout glitches)
in wavelet
space: the corresponding signal, C1(t0... tn), is then subtracted
from the initial data, D: D1 = D - C1. This is the first deglitching step.
- 2.
- detection of the negative components due to dippers: the
multi-scale vision model is applied to D1, hence negative objects
are detected and the reconstructed signal, C2(t0... tn), is
subtracted to the output of the previous step: D2 = D1 -
C2. This is the second deglitching step where throughs following
glitches are corrected.
- 3.
- detection of the positive components due to faders and dippers:
this step must be done carefully, since sources also produce positive
components in the signal. Only positive objects lasting much longer
or much less than the time spent on a given position on
the sky are automatically
considered as glitches. The output signal, C3(t0... tn), is then
subtracted again from the previous signal: D3 = D2 - C3.
- 4.
- detection of a very strong positive signal on scales where
sources are expected. This step is done in preparation for the baseline
subtraction; the final source detection is not done at this stage.
The multiscale vision model is applied to D3 and
strong positive objects with a correct temporal size are
reconstructed: we obtain C4(t0... tn), and we calculate D4 = D3 -
C4.
- 5.
- baseline subtraction: the signal D4 contains only noise and
temporally undetectable faint sources.
The baseline is easily obtained by convolving D4 by
a low frequency pass band filter.
We obtain C5(t0... tn).
- 6.
- The residual noise is obtained by C6 = D4 - C5; its mean value is
zero.
Finally, the set (C1,C2,C3,C4,C5,C6), represents the
decomposition of the signal into its main components. Note also
that the input signal D is equal to the sum of all components:
| 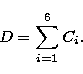 |
(3) |
A deglitched signal is obtained by:
| 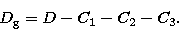 |
(4) |
For faint source detection, we use the signal  ,which is background, dark, and glitch free.
,which is background, dark, and glitch free.
![\begin{figure}
\includegraphics [width=8.8cm,clip]{fig_iso_plot7.ps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg18.gif) |
Figure 4:
These two plots show the signal of a single pixel as a function of time
before calibration (top, flux in ADU) and after calibration (bottom, flux in
ADU/gain/second). The trough following the second glitch (dipper) has
disappeared and the remaining signal contains only Gaussian noise (photon noise
+ readout noise) plus sources (one relatively bright source is located at
readout 120, fainter sources will only appear after co-addition of all pixels
having seen the same sky position in the final map) |
The background has been
subtracted, and glitches with their long duration effects have been
suppressed. Applying the pattern recognition method to all detector
pixels, we obtain a cube  . All other component are kept in
the cubes Ci. The baseline suppression presents several
advantages: first, the final raster map is dark-corrected
without the need of a library dark, since we end up with a mean zero
level for each pixel. This is particularly important when the library
dark is not good enough, and induces visual artifacts
(Starck et al. 1999). Second, the flat-field accuracy only
affects the photometry
of the sources but not the background level, which is extracted in the
baseline. Thus, its influence in the final calibration is decreased.
. All other component are kept in
the cubes Ci. The baseline suppression presents several
advantages: first, the final raster map is dark-corrected
without the need of a library dark, since we end up with a mean zero
level for each pixel. This is particularly important when the library
dark is not good enough, and induces visual artifacts
(Starck et al. 1999). Second, the flat-field accuracy only
affects the photometry
of the sources but not the background level, which is extracted in the
baseline. Thus, its influence in the final calibration is decreased.
Figure 4 (bottom) presents the result obtained with this
method. The decomposition of the original signal
(Fig. 4 top) into its main components is shown in
Fig. 5: (a), (b), and (d) are features subtracted
from the original signal (short glitches, dipper, and
baseline, respectively), which present no direct interest for faint source
detection, and only (c) and (e) (bright sources and noise plus
faint sources, respectively) are kept for building the final image.
The noise must also be kept because faint sources are often detectable
only after co-addition of the data.
![\begin{figure}
\includegraphics [width=13cm,clip]{fig_iso_plot6.ps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg20.gif) |
Figure 5:
Decomposition of the signal into its main components:
a) short glitch, b) trough of a dipper, c) bright source, d)
baseline, e) noise plus faint sources. The simple sum of the fives
components is exactly equal to the original data (see Fig. 2). The
calibrated background free data are obtained by addition of signals
c) and e). Figure c) shows the reconstruction of a source
approximated as a Gaussian, but sources are kept in the signal and
their shape differ from one source to the other |
The
simple sum of the five components is exactly equal to the original
data (see Fig. 4 top). The calibrated background free
data (see Fig. 4 bottom) are then obtained by addition
of (c) and (e).
Three kinds of transients must be distinguished:
- 1.
- a long term transient at the beginning of the observation. It
can be either a downward or an upward transient depending on the
flux level of the previous observation.
If the difference between the present background level (which
dominates the signal in faint source observations) and the previous
background level is high, then the transient can affect several
hundred frames. Long term transients have no effect on source
detection when using the multi-resolution approach, because they are
eliminated with the baseline.
- 2.
- an upward transient each time a pixel points in the direction of
a source. There is presently no physical model which describes the
ISOCAM upward transient. This type of transient affects mainly the
photometry. Objects with a flux at the theoretical detection limit
are not detected because the signal measured is only a fraction
(typically 60%) of the signal after stabilization (Starck et al.
1999).
- 3.
- a downward transient after each source, which can produce ghosts
when following bright sources, since the downward transient may remain
above the noise level even after the change of camera pointing.
For an automatic source detection method, the last type of transient must be
corrected for. Physical models exist for downward transients and
several methods may be used (Starck et al. 1999). In our
case, a very trivial approach can also be used, which consists of
treating the reconstructed temporal objects. Indeed, we can assume
that the part of the object which appears after the displacement of
the array is the transient, and it can be eliminated by a simple
thresholding.
Figure 6 bottom shows the result after such a treatment.
A signal containing a source (top) shows a strong downward transient,
which is very clear after deglitching and baseline subtraction
(middle). The three successive positions on the array are affected by
the transient, which induces ghosts in the final image if they are not
removed. The correct shape of the source (bottom) is obtained through
the technique developed by Abergel et al.
(1996).
![\begin{figure}
\includegraphics [width=8.8cm,clip]{fig_transient.ps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg21.gif) |
Figure 6:
Examples of transient corrections. Top: signal containing a
strong source. Middle: signal after deglitching and subtraction of the baseline.
The dashed line shows the configuration limits and crosses indicate the readouts which
have been masked. Bottom: signal after the transient correction |
The presented method produces good results but requires a long computation
time. A similar but faster method, producing results of
equivalent quality and
avoiding the delicate problem of the negative wings of wavelet
functions, is to use the Multi-Resolution Median Transform (MMT)
(Starck et al. 1998) instead of the wavelet transform. No
confusion between positive and negative objects is possible because this
multi-resolution transform does not present the ringing drawback. The
MMT has been proposed for data compression (Starck et al. 1996),
and it has also recently been used for ISOCAM short glitch suppression
(Starck et al. 1999).
The MMT algorithm is relatively simple. Let med(S,n) be the median
transform of a one-dimensional signal S within a window of dimension
n.
If we define, for  resolution scales, the coefficients:
resolution scales, the coefficients:
|  |
(5) |
| (6) |
we can expand the original signal similarly to the "à trous algorithm'':
| 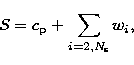 |
(7) |
where  is the residual signal.
is the residual signal.
Applying the multi-scale vision model (MVM) with the MMT, the object
reconstruction is straightforward, because no iteration is needed to
get a good quality reconstruction.
Figure 7 shows the
comparison between the "à trous'' wavelet transform (on the left)
and the MMT (on the right) of the input signal in Fig. 1c.
In these diagrams, the scale is represented as a function of the time.
We can see that with the MMT, it is easier to distinguish
sources from glitches.
Figure 8 shows the result of MVM using the MMT instead
of the "à trous'' algorithm. From (a) to (e), we see
the reconstructed source, the dipper, the baseline,
the sum of the glitches and the baseline (i.e. non-interesting data),
and the original signal from which the signal (d) has been subtracted.
![\begin{figure}
\includegraphics [width=8cm,clip]{fig_wt_glitch1.eps}
\hspace*{1mm}
\includegraphics [width=8cm,clip]{fig_mmt_glitch1.eps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg25.gif) |
Figure 7:
Comparison between the "à trous'' wavelet transform (left) and the
multresolution median transform (right) of the signal of Fig. 1c.
Resolution scale is represented versus the time. We note that the separation between
the source and the glitch is improved using the MMT |
![\begin{figure}
\includegraphics [width=13cm,clip]{fig_glitch_median.ps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg26.gif) |
Figure 8:
Decomposition of the signal into its main components using
the MMT:
a) source, b) dipper, c) baseline,
d) Sum of the glitches and the baseline (i.e. non interesting data),
and e) original signal minus d) |
Once the calibration is done, the raster map
can normally be created, with flat field correction, and all data
co-added. The associated rms map can now be used for the detection,
which was impossible before due to the strong effect of residual
glitches. Since the background has been removed, simple source detection
can be done just by comparing the flux in the raster map to the rms
map.


Up: Faint source detection in
Copyright The European Southern Observatory (ESO)
![]() (where
(where ![]() is the number of readouts
per raster position), while it is divided by
is the number of readouts
per raster position), while it is divided by
![]() (where
(where ![]() is the number of
redundancies inside the raster, i.e. the number of pixels which see
the same sky position) for co-added data.
is the number of
redundancies inside the raster, i.e. the number of pixels which see
the same sky position) for co-added data.
![]() (see Appendix B for more details
about the "à trous'' algorithm)
(see Appendix B for more details
about the "à trous'' algorithm)
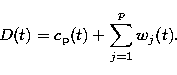
![]() , the wavelet transform operator, and
, the wavelet transform operator, and ![]() , the
projection operator in the subspace of the detected coefficients
(i.e.
, the
projection operator in the subspace of the detected coefficients
(i.e. ![]() set all coefficients at scales and positions where
nothing was detected to zero), the solution can be found by minimizing the
following expression:
set all coefficients at scales and positions where
nothing was detected to zero), the solution can be found by minimizing the
following expression:
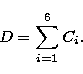
![\begin{figure}
\includegraphics [width=13cm,clip]{fig_iso_plot6.ps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg20.gif)
![]() resolution scales, the coefficients:
resolution scales, the coefficients:

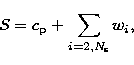
![\begin{figure}
\includegraphics [width=8cm,clip]{fig_wt_glitch1.eps}
\hspace*{1mm}
\includegraphics [width=8cm,clip]{fig_mmt_glitch1.eps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg25.gif)