Once all data have been calibrated, the final raster map R(x,y) and
its associated rms map ![]() can be created. If several
rasters of the same field are available, they can be co-added in order
to improve the signal to noise ratio. The noise in R(x,y) (i.e.
can be created. If several
rasters of the same field are available, they can be co-added in order
to improve the signal to noise ratio. The noise in R(x,y) (i.e.
![]() ) is non-homogeneously distributed over the map,
first because some pixels have been masked (short glitches) and
second because some areas of the field (particularly the border of
the mosaic) present low redundancy (few readouts per sky
position). For this reason the noise around the border of the image
can be relatively
high with respect to the noise toward the image center. Therefore, if we
made the
simple hypothesis of uniform noise (for instance Gaussian noise of
standard deviation
) is non-homogeneously distributed over the map,
first because some pixels have been masked (short glitches) and
second because some areas of the field (particularly the border of
the mosaic) present low redundancy (few readouts per sky
position). For this reason the noise around the border of the image
can be relatively
high with respect to the noise toward the image center. Therefore, if we
made the
simple hypothesis of uniform noise (for instance Gaussian noise of
standard deviation ![]() ), it would lead to a large amount of false
detections on the border. The correct solution is to use the
), it would lead to a large amount of false
detections on the border. The correct solution is to use the
![]() map. In order to detect faint sources on the final
image, we can use the multi-scale vision model (MVM) in
two-dimensions. This time we use the "à trous'' algorithm because the
linearity of the wavelet transform allows us to derive a robust
modelling of the noise in wavelet space (using the rms map
map. In order to detect faint sources on the final
image, we can use the multi-scale vision model (MVM) in
two-dimensions. This time we use the "à trous'' algorithm because the
linearity of the wavelet transform allows us to derive a robust
modelling of the noise in wavelet space (using the rms map
![]() ), which is impossible using the MMT. Moreover, in this
case the artefacts around sources are negligible since we have no
strong sources.
), which is impossible using the MMT. Moreover, in this
case the artefacts around sources are negligible since we have no
strong sources.
For each wavelet coefficient wj(x,y) of R, the exact
standard deviation ![]() has to be calculated from the root
mean square map
has to be calculated from the root
mean square map ![]() .
.
A wavelet coefficient wj(x,y) is obtained by the correlation
product between the image R and a function gj:
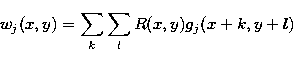 |
(8) |
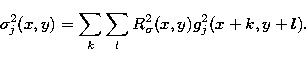 |
(9) |
| (10) |
| (11) |
Finally, the outputs of PRETI are numerous and contain all information at all scales divided into several cubes of data and images in FITS format, but the most commonly used outputs are the following:
A field where this faint source detection method is widely applied is the study
of source number counts in galaxy surveys, as for example the ISOCAM
survey in the Hubble Deep Field region (Aussel et al. 1999).
We will explain in the next section how simulations allows us
to determine the accuracy of the so called ![]() diagrams,
which show the number N of sources as a function of the emitted flux S.
diagrams,
which show the number N of sources as a function of the emitted flux S.
![\begin{figure}
\includegraphics [width=8cm,clip]{imabruit.eps}
\hspace*{2mm}
\includegraphics [width=8cm,clip]{imasrc.eps}\end{figure}](/articles/aas/full/1999/14/ds8374/Timg40.gif) |
Figure:9
Simulation of the ISO-HDF mosaic (I): (left) this image
contains only simulated photon noise plus readout noise, i.e. Gaussian
noise, (right) image of the ISO-HDF mosaic without any noise and with
simulated sources according to a distribution without
evolution (Franceschini 1997).
Sources ranges from |
Copyright The European Southern Observatory (ESO)