To understand where and how integrated optics can play a role in astronomical interferometry, we review the different optical functions present within an interferometer (see Fig. 1). This comes after a summary of stellar interferometry principles. All interferometers but GI2T being single-mode beam combiners (the field is limited to the diffraction pattern of each aperture), we limit our study to the single-mode field, the most appropriate mode for integrated optics.
A two-telescope stellar interferometer provides the measure of interference
fringes between two beams at the spatial frequency ![]() , where
, where
![]() is the wavelength, and B the projection of the baseline vector
is the wavelength, and B the projection of the baseline vector
![]() defined by the two telescopes along
defined by the two telescopes along ![]() the unit vector
pointing to the source. The complex visibility of these fringes
is proportional to the Fourier transform of the object intensity
distribution (Van-Cittert Zernike theorem). Hereafter we call
visibility V the modulus of the degree of coherence at the spatial
frequency
the unit vector
pointing to the source. The complex visibility of these fringes
is proportional to the Fourier transform of the object intensity
distribution (Van-Cittert Zernike theorem). Hereafter we call
visibility V the modulus of the degree of coherence at the spatial
frequency ![]() normalized to the value at the zero
frequency,
normalized to the value at the zero
frequency,
 |
(1) |
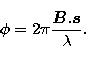 |
(2) |
The stellar light is collected by each individual aperture. These apertures can be either siderostats (e.g. Mark III, PTI, IOTA) or telescopes (e.g. GI2T, VLTI, Keck Interferometer). The coverage of the spatial frequencies is usually done by carefully locating the apertures in order to take advantage of the earth rotation which induces a variation of the length and orientation of the projected baselines (super-synthesis effect). If the structure of the object does not depend on wavelength, then observing at different wavelengths is equivalent to observing at different spatial frequencies. When the apertures are movable (GI2T, IOTA, SUSI), the interferometer can cover many different baselines with different geometrical configurations.
The beams coming out from each telescope must be directed toward the beam combination table. Two different techniques can achieve this transportation:
Flat mirrors are usually used to carry the light from the single apertures toward the central beam combiner. Their main advantages are high throughput and low wavelength dependency. However they are sensitive to thermal and mechanical disturbance and they require many degrees of freedom to align the beams.
Two different philosophies have been developed for transportation. 1) The Coudé trains are symmetrical to prevent differential polarization rotations and phase shifts. It leads to a large number of mirrors and thus a low throughput especially in the visible. One still get residual polarization effects essentially due to optical coatings differences which are not negligible. 2) The number of optics is reduced to a minimum and the large resulting polarization effects are calibrated and corrected inside the interferometer (Sect. 2.4).
[Froehly (1981)] and [Connes et al. (1984)] were the first to propose fiber optics to
connect different apertures. Major efforts have been achieved in this
field by [Shaklan & Roddier (1987),Shaklan (1990),Reynaud et al. (1994),Reynaud & Lagorceix (1996)] with silica fibers and in the
2.2 ![]() m range by [Coudé du Foresto & Ridgway (1991),Coudé du Foresto et al. (1996)] with fluoride fibers.
m range by [Coudé du Foresto & Ridgway (1991),Coudé du Foresto et al. (1996)] with fluoride fibers.
The optical fiber throughput is very high: 100-m silica fiber has a
throughput of ![]() at
at ![]() (0.15 dB/km). In addition,
fibers offer some flexibility since the only degrees of freedom are
located at the entrance and output of the fiber. That is one reason why
[Turner & Brummelaar (1997)] have proposed optical fibers to combine the visible beams
of CHARA. Using fibers can be significantly less expensive than bulk
optics.
(0.15 dB/km). In addition,
fibers offer some flexibility since the only degrees of freedom are
located at the entrance and output of the fiber. That is one reason why
[Turner & Brummelaar (1997)] have proposed optical fibers to combine the visible beams
of CHARA. Using fibers can be significantly less expensive than bulk
optics.
The several drawbacks of using optical fibers are: chromatic dispersion if the optical path through the different fibers is not matched; mechanical and thermal sensitivity (optical fibers are also used as micro-sensors); and birefringence of the material. However [Reynaud & Lagorceix (1996)] have shown that one can overcome most of these difficulties by controlling actively the fiber length, carefully polishing the fiber ends and by using polarization maintaining fibers.
The optical path from the beam combiner upward to the stellar source are not identical for each beam. The interferometer must equalize the pathlength at the micron-level accuracy. Furthermore the path lengths change with time and the interferometer must take into account the sidereal motion. This optical function is performed with delay lines.
The classical solution consists in a retro-reflector based on a moving chart [Colavita et al. (1991)]. The retro-reflector can be either a cat's eye or a corner cube. [Reynaud & Delaire (1994),Zhao et al. (1995)] have proposed to stretch optical fibers to delay the optical path. Laboratory experiments showed that this type of delay lines can achieve more than 2 m continuous delay with 100 m silica fibers [Simohamed & Reynaud (1996)], and about 0.4 mm continuous delay with 3.4 m fluoride fibers [Zhao et al. (1995)]. However in the latter case, the maximum optical path delay is somewhat limited since the fiber length is restricted to the maximal accepted stretch: [Zhao et al. (1995),Mariotti et al. (1996)] proposed multi-stage delay lines which perform short continuous delays by fiber stretching and long delays by switching between fiber arms of different lengths. However the differential dispersion in fibers of different length still remains a limiting factor of this technology.
Optical path modulation using silica fibers has been implemented in the ESO prototype fringe sensor unit [Rabbia et al. (1996)].
The stellar light goes through the atmosphere where the wavefront is disturbed. Depending on the wavelength and the size of the turbulent cell (r0) compared to the aperture size, the incoming wavefront is corrugated and the stellar spot divided in several speckles with phase differences in the focal plane. Single-mode interferometers select only one speckle and therefore the atmospheric turbulence leads to signal losses proportional to the Strehl ratio. Using adaptive optics to correct at least partially the incoming wavefront increases the total throughput of an interferometer. The minimum wavefront correction is the tip-tilt correction used on many interferometers (IOTA, SUSI, PTI, ...)
Due to the same atmospheric perturbations but at the baseline scale, the optical path between two apertures will rapidly vary. When requiring a high sensitivity like for spectral analysis, one needs to increase the acquisition time. The interferometric signal must be analyzed faster than the turbulence time scale to prevent visibility losses due to fringe blurring. The fringe tracker analyzes the fringe position and actively control a small delay line to compensate the atmospheric delay. The fringes are stabilized.
Instrumental polarization can dramatically degrade the fringe visibility. The main effects are differential rotations and phase shifts between the polarization directions [Rousselet-Perraut et al. (1996)]. Even if special care is taken in designing the optical path to have the most symetrical path for each beam, in practice the incident angles are not exactly the same and the mirrors do not have the same coatings.
Differential rotations can be compensated by rotator devices [Rousselet-Perraut et al. (1998)] whereas differential phase shifts can be corrected by Babinet compensators [Reynaud (1993)] or Lefèvre fiber loops [Lefèvre (1980)].
The incoming wavefronts propagate through a spatial filter, a geometrical
device which selects only one coherent core of the beams. It can be
achieved either by a micrometer-sized hole or by an optical waveguide
like a fiber [Shaklan & Roddier (1988)]. This principle has been applied successfully
to the FLUOR interferometric instrument [Coudé du Foresto (1996)]. The beams
including atmospheric turbulence effects are then characterized by only
two quantities, the amplitude and the phase of the outcoming electric
field![]() . Combined with
photometric calibration, this process leads to accurate visibilities (see
Sect. 2.5).
. Combined with
photometric calibration, this process leads to accurate visibilities (see
Sect. 2.5).
| Figure 2: The different types of beam combination in classical optics with the profile of the output intensity |
[Mariotti et al. (1992)] have classified the different types of beam combinations. In the single-mode case, there are two types of beam combination:
In bulk optics, the co-axial combination is performed with a beam splitter whereas the multi-axial combination is done by focusing the different beams on the same spot. In the case of multi-axial combination, the differential tilt between the beams produces fringes on the point spread function. The co-axial combination can be regarded as a particular case of the multi-axial mode where all the beams are superposed without tilts: the fringes disappears and the amplitude of the resulting spot depends on the phase difference between the two beams.
The fringe encoding is achieved, in the co-axial case, by modulating the
optical path difference between the two beams which results in an intensity
modulation, or, in the multi-axial case, by sampling the spatial fringes
with a detector matrix![]() . Usually if the fringes are coded in one direction, the
other direction is compressed to reduce the number of pixels.
. Usually if the fringes are coded in one direction, the
other direction is compressed to reduce the number of pixels.
The spectral information can be obtained by dispersing the fringes with a dispersive element (GI2T, PTI). Mariotti & Ridgway (1988) also suggested to apply the concept of Fourier transform spectrography to interferometry by performing double Fourier transform interferometry.
In the visible, the detectors are either CCDs or photon-counting cameras. In the infrared, for long mono-pixel InSb detectors have been used, but with the availability of array detectors with low read-out noise, interferometers started to use detector matrices.
Copyright The European Southern Observatory (ESO)