In our search for multiperiodicity in the selected ![]() Cen data sets we
applied the Fourier analysis and two methods that try to get rid of
aliases due to data sampling. They are the CLEAN (Roberts et al. 1987) and the
CLEANEST (Foster 1995) algorithms implemented in a SUN workstation by Emilio
(1997). Both methods are based on modeling the observed data in Fourier space
as a combination of trial trigonometric functions. CLEANEST is more powerful,
because it uses more than one trial function simultaneously. In the case of our
spectroscopic data, frequency analysis was performed
on each of the individual time series formed by data at each resolution step
across the He I
Cen data sets we
applied the Fourier analysis and two methods that try to get rid of
aliases due to data sampling. They are the CLEAN (Roberts et al. 1987) and the
CLEANEST (Foster 1995) algorithms implemented in a SUN workstation by Emilio
(1997). Both methods are based on modeling the observed data in Fourier space
as a combination of trial trigonometric functions. CLEANEST is more powerful,
because it uses more than one trial function simultaneously. In the case of our
spectroscopic data, frequency analysis was performed
on each of the individual time series formed by data at each resolution step
across the He I ![]() 667.8 nm line profile. The lpv were also
analysed
with the Fourier-Doppler Imaging technique (FDI) (KWM). In that method, the
temporal variations of the line profile series are transformed in both time and
Doppler space; a two-dimensional Fourier representation of the variations is
thus obtained, where the frequencies along the velocity axis can be identified
with the degrees l rather than with the (apparent) azimuthal orders
(Gough, private communication to Kennelly et al. 1997).
667.8 nm line profile. The lpv were also
analysed
with the Fourier-Doppler Imaging technique (FDI) (KWM). In that method, the
temporal variations of the line profile series are transformed in both time and
Doppler space; a two-dimensional Fourier representation of the variations is
thus obtained, where the frequencies along the velocity axis can be identified
with the degrees l rather than with the (apparent) azimuthal orders
(Gough, private communication to Kennelly et al. 1997).
High order lpv is quite conspicuous in ![]() Cen. Additional low-order
lpv is also strongly present, as it can be seen in the peculiar average
stellar line profile (see Fig. 1).Variations in line depth at the
Cen. Additional low-order
lpv is also strongly present, as it can be seen in the peculiar average
stellar line profile (see Fig. 1).Variations in line depth at the ![]() 1-2%
level in time scales of
1-2%
level in time scales of ![]() 5 min are also observed in the central region of
the HeI
5 min are also observed in the central region of
the HeI ![]() 667.8 nm line. They are probably due to intrinsic Be-type
variations probably arising in the circumstellar disk, not linked to NRP.
667.8 nm line. They are probably due to intrinsic Be-type
variations probably arising in the circumstellar disk, not linked to NRP.
The CLEAN algorithm was applied to each of the 385 residual time series formed by subtracting the global mean spectrum of the observing run from each individual spectrum, and following the procedure of Gies & Kullavanijaya (1988). The gain was set at 0.8. The main peaks were identified after a few iterations, and there were no significant changes afterwards; we thus limited to 10 the number of iterations. A CLEANed periodogram at each position across the line is shown in Fig. 1 with the global average profile in the lower panel. Frequencies separated by 1 c/d can be combinations of a true frequency and an alias that CLEAN could not eliminate.
Indeed, the sequences ![]() 0.3/1.3/3.3 and 1.7/2.7/3.7 c/d
never occur together at any wavelength; only one of the frequencies of each
group is probably present in the star.
0.3/1.3/3.3 and 1.7/2.7/3.7 c/d
never occur together at any wavelength; only one of the frequencies of each
group is probably present in the star.
We also applied the CLEANEST algorithm (Foster 1995) to our 385 time series across the line profile. This algorithm requires the number of frequencies to be defined a priori. We found that the clearest two-dimensional pattern is obtained by searching for just two frequencies. Since the method is applied to each of the 385 wavelength bin time series, more than two frequencies will show up (if more than two are present). In fact, we constructed two distinct residuals time series. A first one was formed by subtracting the global mean spectrum of the observing run from each individual spectrum; for the second one, we subtracted the mean nightly profile from each spectrum. For the first time series, lower frequencies are enhanced, while higher frequencies are more easily distinguished in the second series. Figure 2a shows the results of CLEANEST using the global mean spectrum; the corresponding periodogram summed across the wavelength axis is shown in Fig. 2b. The same is presented in Figs. 3a,b, but now using the nightly mean spectrum to form the residuals. Note that the algorithm was not able to eliminate completely the 1-day aliases.
The FDI method (KWM) was also applied to the 385 time series across the line
profile. This technique maps the residuals onto a space where the coordinates
are the time frequency and the normalized wavelength frequency, provided that
the wavelength is mapped onto stellar longitude ![]() using:
using:
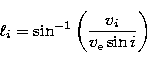 |
(1) |
where vi is the velocity corresponding to the wavelength bin i
with respect to the center of the line (KWM). It can be shown that the
normalized wavelength frequency corresponds to the pulsation degree l.
In the case of sectoral modes, it will naturally be equal to
![]() . The main advantage of this technique is that it
decomposes
complex patterns of multiple modes. However, great care must be taken in the
interpretation of the results, since simulations indicate that there is not a
one-to-one relationship between an oscillation mode and its representation in
Fourier space (e.g. Kennelly et al. 1997).
The FDI was applied to the two residual time series as was done with CLEANEST. The projected rotational velocity is determined in
Sect. 4.1.
The variations of the line
profile overall shape were decomposed by the FDI method into very strong
low-degree pulsation modes (l = 2, 4), although higher degree modes up
to
. The main advantage of this technique is that it
decomposes
complex patterns of multiple modes. However, great care must be taken in the
interpretation of the results, since simulations indicate that there is not a
one-to-one relationship between an oscillation mode and its representation in
Fourier space (e.g. Kennelly et al. 1997).
The FDI was applied to the two residual time series as was done with CLEANEST. The projected rotational velocity is determined in
Sect. 4.1.
The variations of the line
profile overall shape were decomposed by the FDI method into very strong
low-degree pulsation modes (l = 2, 4), although higher degree modes up
to ![]() 15 can also be seen. In spite of the fact that the
two-dimensional map is hampered by one-day aliases in the time frequency
direction, the main frequencies coincide with that produced by CLEANEST.
15 can also be seen. In spite of the fact that the
two-dimensional map is hampered by one-day aliases in the time frequency
direction, the main frequencies coincide with that produced by CLEANEST.
In order to examine the nightly variations, we also applied the CLEANEST and
FDI methods to each night separately. In our case, the low limit time frequency
that can be determined from each night is about 5.5 c/d (corresponding to
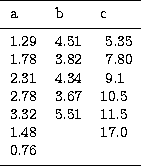
![]() 4.4 h nightly observing runs). The results are shown in Table 2 and
Fig. 4 for nights May 15, 16. Note the changing pattern from night to night.
In fact, for nights 11,
15 and 17 the two-dimensional map is apparently dominated by a mode with
l =
4.4 h nightly observing runs). The results are shown in Table 2 and
Fig. 4 for nights May 15, 16. Note the changing pattern from night to night.
In fact, for nights 11,
15 and 17 the two-dimensional map is apparently dominated by a mode with
l = ![]() 2,
whereas for nights 12, 16 and 18 a mode with
2,
whereas for nights 12, 16 and 18 a mode with ![]() 4 is by far
the strongest. However, one must be cautious about the quantitative aspect of this interpretation,
because signals with frequencies
4 is by far
the strongest. However, one must be cautious about the quantitative aspect of this interpretation,
because signals with frequencies ![]() 5.5 c/d are incompletely observed on a given night
(see Sect. 4.3).
5.5 c/d are incompletely observed on a given night
(see Sect. 4.3).
This apparent mode alternation will be discussed later (see the
Discussion). For reasonable values of the stellar rotation frequency (see
Sect. 4.1), high intensity modes lie generally above the non-propagating
line, namely ![]()
![]() , which defines the position of
surface phenomena that are locked to the stellar rotation. Those modes
would thus correspond to prograde modes.
Taking into account the extension in wavelength of occurrence of each frequency
and from the power spectra summed across the wavelength axis (see Figs. 2b and
3b), the main detected periodicities are summarized in Table 2. Other weak
modes also appear at higher frequencies. For the moment, we will not discuss which
frequencies are really present in the star; it appears clear, however, that even
CLEANEST is not capable of eliminating all aliases due to data sampling. It is worth noting that the
spectroscopic coverage is 1.07 days observed in total over a time span of 7.16 days. Clearly the large
gaps in sampling cause significant ambiguities to exist in extracting the actual power spectrum from
the data.
, which defines the position of
surface phenomena that are locked to the stellar rotation. Those modes
would thus correspond to prograde modes.
Taking into account the extension in wavelength of occurrence of each frequency
and from the power spectra summed across the wavelength axis (see Figs. 2b and
3b), the main detected periodicities are summarized in Table 2. Other weak
modes also appear at higher frequencies. For the moment, we will not discuss which
frequencies are really present in the star; it appears clear, however, that even
CLEANEST is not capable of eliminating all aliases due to data sampling. It is worth noting that the
spectroscopic coverage is 1.07 days observed in total over a time span of 7.16 days. Clearly the large
gaps in sampling cause significant ambiguities to exist in extracting the actual power spectrum from
the data.
 |
The CLEAN and CLEANEST algorithms have also been applied to the time series
formed by the individual measurements of the radial velocity (RV), full width
at half maximum (FWHM), and equivalent width (EW) of our HeI line
observations. These parameters have been measured using standard IRAF
procedures. Those two algorithms have also been used to analyse the temporal
series of RV, FWHM and EW data measured by SBHB in SiIII ![]() 455.26 nm
line profiles of
455.26 nm
line profiles of ![]() Cen. The main frequencies found in these analyses are shown in Table 3.
Cen. The main frequencies found in these analyses are shown in Table 3.
We have searched for periodic variations in five different sets of photometric
data (ground based using Strömgren b filter): (1) data published by Cuypers et al. (1989) corresponding to
observations made in 1987 and (2) in 1988, (3) Hipparcos data,
obtained between early 1990 and August 1992, (4) data published by SBHB,
corresponding to observations collected in 1992 and (5), observations obtained at LNA in 1993. The temporal analysis of
these data sets was equally performed using both the CLEAN and CLEANEST
algorithms, except for Hipparcos data which have been analysed with CLEAN. In
Fig. 5 we show the dirty spectrum and the periodogram of LNA May-August 1993
data, obtained with CLEAN. The typical uncertitude on the frequencies detected
in our photometric data is ![]() 0.08 c/d, corresponding to the FWHM of the
peaks
in the periodogram. The main frequencies found in five data sets are:
0.08 c/d, corresponding to the FWHM of the
peaks
in the periodogram. The main frequencies found in five data sets are:
![\begin{figure}
\includegraphics [width=8.8cm]{1580f5a.eps}
\includegraphics [width=8.8cm]{1580f5b.eps}\end{figure}](/articles/aas/full/1999/12/ds1580/Timg32.gif) |
Figure 5: a) Dirty spectrum for photometric measurements obtained at LNA (May-August 1993). b) Corresponding CLEANed periodogram |
Copyright The European Southern Observatory (ESO)