It should be mentioned that the evaporation problem is closely related to an often discussed
criticism of the photodissociation pump mechanism. The evaporation rate is responsible for the
replacement of the large amount of gaseous water that is destroyed by photodissociation.
Only with sufficient evaporation going on for an extended time the masers can operate without
turning off. In the present
stationary maser model the evaporation rate ![]() equals the number of water molecules
destroyed
per
equals the number of water molecules
destroyed
per ![]() and second (see Eq. (2)). An evaporation rate of
and second (see Eq. (2)). An evaporation rate of ![]() is necessary if e.g. 107 water
molecules are destroyed per
is necessary if e.g. 107 water
molecules are destroyed per ![]() and second! The question is whether such high
evaporation rates are possible at all.
The stationary maser model given here implies a highly dynamical equilibrium between
evaporation and destruction in which the densities of OH and
and second! The question is whether such high
evaporation rates are possible at all.
The stationary maser model given here implies a highly dynamical equilibrium between
evaporation and destruction in which the densities of OH and ![]() adjust to the given
photodissociation rates. In this suggested mechanism the evaporated water is converted to
translationally hot hydrogen atoms and relatively low oxygen atoms by the VUV radiation
from the central star and heats the environment in areas where water is evaporated
("photolytic
heating").
adjust to the given
photodissociation rates. In this suggested mechanism the evaporated water is converted to
translationally hot hydrogen atoms and relatively low oxygen atoms by the VUV radiation
from the central star and heats the environment in areas where water is evaporated
("photolytic
heating").
The region around the star that is exposed to the direct heat- and VUV- flux from the star will
reach out only to a region where small grains are present in high abundance. With a grain
density of ![]() for
for ![]() grains, which is considered to be typical
for cold interstellar
clouds, an optical density of
grains, which is considered to be typical
for cold interstellar
clouds, an optical density of ![]() is
obtained. This implies that the radiation will
be attenuated to 1/e along a distance of only
is
obtained. This implies that the radiation will
be attenuated to 1/e along a distance of only ![]() AU. This thin layer of a few AU
thickness blocks the direct radiation. Although the radiation will diffuse further out, it is
expected
that there will be no VUV beyond that border. We will use the term "small grain border" for
this thin layer below.
AU. This thin layer of a few AU
thickness blocks the direct radiation. Although the radiation will diffuse further out, it is
expected
that there will be no VUV beyond that border. We will use the term "small grain border" for
this thin layer below.
The small grains at this border are exposed to the direct heat flux from the star and
will be evaporated with time leading to a growth of the HII region. The time until complete
evaporation increases with the size of the grains. If the small ![]() grains are already
completely evaporated larger grains will remain at the inner side of the small grain border.
Because their evaporation takes a longer time they will be a source of gas phase water
molecules which are exposed to the VUV field from the central star. If we assume in addition
that the grains move with
their gravitational velocity towards the star large grains will penetrate deeper into the HII
region than small grains. Because the optical density of the remaining large grains is much
lower than that for the small grains at the border they are exposed to the direct heat- and
VUV- flux from the star. This increases with
decreasing distance to the star. Consequently evaporation and photolysis of water takes place
simultaneously in this regions and yields the astrophysical
situation where the present maser model applies. Below we will discuss the processes that
occur to the larger grains at the inner side of the small gain border in more detail.
grains are already
completely evaporated larger grains will remain at the inner side of the small grain border.
Because their evaporation takes a longer time they will be a source of gas phase water
molecules which are exposed to the VUV field from the central star. If we assume in addition
that the grains move with
their gravitational velocity towards the star large grains will penetrate deeper into the HII
region than small grains. Because the optical density of the remaining large grains is much
lower than that for the small grains at the border they are exposed to the direct heat- and
VUV- flux from the star. This increases with
decreasing distance to the star. Consequently evaporation and photolysis of water takes place
simultaneously in this regions and yields the astrophysical
situation where the present maser model applies. Below we will discuss the processes that
occur to the larger grains at the inner side of the small gain border in more detail.
For a single grain the evaporation is determined mainly by its surface area and temperature. The surface temperature depends on the heat transfer from and to the surface. The heat transferred to the surface results from the direct heat flux from the star and from collisions with the surrounding gas, including e.g. the heat resulting from the adsorption of water or atoms that are generated by photolytic heating. The heat losses result from black body radiation, heat conduction to the bulk and evaporative cooling by desorption.
The evaporation of grains is extremely difficult to predict quantitatively because it depends on too many and mostly unknown parameters. Features like porosity or chemical composition of the surface strongly affect surface area and temperature leading to large variations in the evaporation rate. This problem is well known from comets (e.g. [Combi et al.] 1998; [Schultz et al.] 1992) where the identical problem is encountered. The astrophysical problem of the evaporation from grains near new born stars may also be compared with the evaporation of droplets in spray combustion where large difficulties are encountered in a quantitative treatment despite massive experimental and theoretical efforts. Because it is impossible to derive quantitative evaporation rates we restrict ourselves to a qualitative discussion of evaporation immediately from the analogy with spray combustion. The large droplets survive longer than small droplets in spray evaporation and penetrate deeper into the gas.
There are nevertheless some important qualitative conclusions which can be drawn. Here larger grains live longer when they are exposed to the direct heat flux from the star and penetrate the HII region deeper than the small grains. Closer to the star they are exposed to an increasing heat flux, acquire larger temperatures and may yield rather high evaporation rates in the presence of intense VUV radiation there.
To determine the evaporation rate ![]() both the desorption flux
density
both the desorption flux
density ![]() and the
surface area of all grains in
and the
surface area of all grains in ![]() maser volume have to be known. The desorption flux density is
closely related to the vapour pressure of ice. Under thermal equilibrium conditions the same
number of water molecules are adsorbed and desorbed on the surface, i.e., the desorption flux
density
maser volume have to be known. The desorption flux density is
closely related to the vapour pressure of ice. Under thermal equilibrium conditions the same
number of water molecules are adsorbed and desorbed on the surface, i.e., the desorption flux
density ![]() equals the adsorption flux density
equals the adsorption flux density ![]() . We approximate the
adsorption flux density
by
. We approximate the
adsorption flux density
by ![]() with the gas phase density n = p/kT and velocity
with the gas phase density n = p/kT and velocity ![]() . This implies
. This implies
![]() with the vapour pressure
p of ice. For the vapour pressure p
of ice we use
the well known standard expression
with the vapour pressure
p of ice. For the vapour pressure p
of ice we use
the well known standard expression ![]() ([Handb. of Chem. Phys.]).
With
([Handb. of Chem. Phys.]).
With ![]() and
and ![]() this yields
this yields
| |
(25) |
The evaporating grains have a finite life time that is determined by their surface temperature
and their mass. In this qualitative discussion we neglect adsorption which would yield an even
longer life time.
Because ![]() is the number
is the number ![]() of water molecules desorbing from the grain in
the time
of water molecules desorbing from the grain in
the time ![]() ,
we have
,
we have ![]() . With the density
. With the density ![]() of ice, the total number of water
molecules on a grain is
of ice, the total number of water
molecules on a grain is ![]() under the
assumption of spherical grains.
Therefore
under the
assumption of spherical grains.
Therefore ![]() which yields
which yields
![]() .
This simple model yields a decrease of the grain radius with time that is independent
of the grain radius:
.
This simple model yields a decrease of the grain radius with time that is independent
of the grain radius:
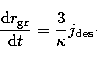 |
(26) |
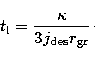 |
(27) |
| (28) |
It is an obvious but important result that small grains are evaporated much faster than large grains and that large grains penetrate deeper. The same effect occurs as mentioned above in the evaporating sprays in Diesel engines where big droplets live much longer than small droplets and penetrate much deeper into the hot gas. This is well known to create one of the most important problems in Diesel combustion, i.e., soot formation which is avoided in modern engines today by the generation of finer droplets.
The importance of the above consideration should be stressed again: The larger water carrying grains penetrate the HII region and are evaporated in a region where they are exposed to the VUV radiation field. Large grains, like comets, may penetrate very deep in the HII region where the heat flux goes up and massive evaporation of water molecules sets in and intense VUV radiation fields are present for sure. This yields the astrophysical situation in which grains are exposed to the heat- and VUV- flux from the star, the situation in which our maser model applies.
First we treat the region close to the border of the small grain region. We calculate the grain
density required for the evaporation rate of ![]() that was
used above to discuss j=3/2
masers. We assume a temperature of 120 K and obtain, according to
Eq. (1), this rate
that was
used above to discuss j=3/2
masers. We assume a temperature of 120 K and obtain, according to
Eq. (1), this rate
![]() with
with
![]() . This surface area (per
. This surface area (per ![]() maser
volume) originates from a grain
size distribution that is not known. If we assume spherical
maser
volume) originates from a grain
size distribution that is not known. If we assume spherical
![]()
![]() grains the
required surface of
area
grains the
required surface of
area ![]() is obtained with a grain density of
is obtained with a grain density of ![]()
![]() . Much lower
grain densities would result for highly porous grains. If we compare these grain densities to the
often used grain density of
. Much lower
grain densities would result for highly porous grains. If we compare these grain densities to the
often used grain density of ![]() for
for ![]() grain in cold clouds, this does not seem to
be too exotic.
grain in cold clouds, this does not seem to
be too exotic.
This implies that a gain of ![]() is obtained for the j=3/2 maser with e.g. a
moderate grain
density of only 24 grains with
is obtained for the j=3/2 maser with e.g. a
moderate grain
density of only 24 grains with ![]() radius in a volume of
radius in a volume of ![]() . These
. These
![]() grains would
live at T=120 K for roughly 30 years and penetrate the HII region 30 AU in this time. The
continuous flow of grains towards the star could thus replaces the grains that are evaporated or
the masers may simply move outwards with the expansion velocity of the HII region. This
mechanism implies that the ground state masers can last as long as the cloud surrounding the
HII region is not expanded so much that the evaporation and
photodissociation rate become too small.
grains would
live at T=120 K for roughly 30 years and penetrate the HII region 30 AU in this time. The
continuous flow of grains towards the star could thus replaces the grains that are evaporated or
the masers may simply move outwards with the expansion velocity of the HII region. This
mechanism implies that the ground state masers can last as long as the cloud surrounding the
HII region is not expanded so much that the evaporation and
photodissociation rate become too small.
According to this picture the ground state OH masers could result from the evaporation of
grains e.g. in the range of ![]() that lie in the circumstellar shell at the inner side of the
small
grain border. In this situation large maser tube lengths of several 100 AUs are possible
tangentially to the border, i.e. large gain lengths are possible which in turn can yield intense
ground state masers.
that lie in the circumstellar shell at the inner side of the
small
grain border. In this situation large maser tube lengths of several 100 AUs are possible
tangentially to the border, i.e. large gain lengths are possible which in turn can yield intense
ground state masers.
As mentioned above the high evaporation rate used above
(e.g. ![]() ) for the single
intense maser spot given by [Baudry & Diamond] (1998) is much more difficult to explain: this evaporation
rate is 3000 times higher than that assumed for the ground state masers. This high evaporation
rate assumed for the
13.44 GHz maser can be explained qualitatively on the basis of the above discussion and the
speculation that this maser is located very close to the star, e.g. at a distance of less than
200 AUs.
This speculation is based on the location of the maximum of the 23.8 GHz continuum map,
where according to [Baudry & Diamond] (1998) the star is suspected to be. It is interesting to note that with
this location of the star most of the j=3/2 masers seem to be indeed at a distance of
) for the single
intense maser spot given by [Baudry & Diamond] (1998) is much more difficult to explain: this evaporation
rate is 3000 times higher than that assumed for the ground state masers. This high evaporation
rate assumed for the
13.44 GHz maser can be explained qualitatively on the basis of the above discussion and the
speculation that this maser is located very close to the star, e.g. at a distance of less than
200 AUs.
This speculation is based on the location of the maximum of the 23.8 GHz continuum map,
where according to [Baudry & Diamond] (1998) the star is suspected to be. It is interesting to note that with
this location of the star most of the j=3/2 masers seem to be indeed at a distance of
![]() AUs, where we assume the small grain border to be.
AUs, where we assume the small grain border to be.
We assume, as before for the j=3/2 masers, that the j=7/2 maser is pumped by evaporation
from water containing grains. In this case, however, the grains must have traveled from
1000 AU to 200 AU and still evaporate water. Therefore the "grains" must be very large
because they survived the increasingly massive evaporation on their way towards the star.
Because a time of roughly 800 years is required to travel the distance of 800 AU only very big
"grains", like comets or planets, survive this journey. We assume an average temperature of
200 K for a "grain" with radius 20 km approaching the star to estimate its life time. With the
desorption flux ![]() at 200 K this yields a life time of
at 200 K this yields a life time of
![]() years and at
800 AUs the "grain" would still have a radius of 10 km. The situation described here is in
closest analogy to comets that approach the sun and yield high water evaporation rates there.
years and at
800 AUs the "grain" would still have a radius of 10 km. The situation described here is in
closest analogy to comets that approach the sun and yield high water evaporation rates there.
At 200 AU, however, the temperature of this 10 km block can be considerably higher, in
particular because the continuously increasing photolytic heating. Without any better
knowledge we discuss an example with a temperature of 250 K for the 10 km block at 200 AU
to explain the high evaporation rate of ![]() . With the desorption flux
. With the desorption flux
![]() we obtain
we obtain ![]() to explain this evaporation rate. Under the
assumption of 10 km
"grains" this requires a "grain" density
to explain this evaporation rate. Under the
assumption of 10 km
"grains" this requires a "grain" density ![]() .
.
This means that one block of 10 km radius is in a volume of ![]() or an
average distance
between these blocks of
or an
average distance
between these blocks of ![]() . For this grain density a mass of
. For this grain density a mass of ![]() is contained in the
tubular maser volume of
is contained in the
tubular maser volume of ![]() that was assumed above for the single intense 13.44 GHz
maser spot by [Baudry & Diamond] (1998). With the mass
that was assumed above for the single intense 13.44 GHz
maser spot by [Baudry & Diamond] (1998). With the mass ![]() of Earth this
implies that one third
of the mass
of earth is contained in the maser volume. For "grains" with
of Earth this
implies that one third
of the mass
of earth is contained in the maser volume. For "grains" with ![]() higher porosity much less
mass is required in the maser volume. These porous grains may survive the passage because of
poor heat conduction to the inner part of the grain. Because the j=7/2 masers are observed
only once in the interstellar medium the somewhat exotic assumptions made here appear not to
be too unreasonable.
higher porosity much less
mass is required in the maser volume. These porous grains may survive the passage because of
poor heat conduction to the inner part of the grain. Because the j=7/2 masers are observed
only once in the interstellar medium the somewhat exotic assumptions made here appear not to
be too unreasonable.
One last remark is related to the probability for the appearance of a particular maser. This probability is determined not only by the gain but also by the probability for spontaneous emission, which clearly favours the excited state masers. On the other hand excited state masers require much larger evaporation rates than the ground state masers. Because these high evaporation rates are not available near the relatively cold border of the HII region the excited state masers should be much closer to the star where the heating of grains increases. The ground state masers on the other hand require neither high evaporation nor high photodissociation rates. If they are located at the border of the HII region they have long tube length and can nevertheless start even by spontaneous emission. Closer to the star, where the evaporation is high, the excited state masers may operate as amplifiers with e.g. the 20 mJy background radiation observed for the 13441 MHz maser.
Copyright The European Southern Observatory (ESO)