Here we assume that grains are exposed to the heat flux from the star and will evaporate water. The term heat flux describes the total amount of energy from the star which heats the grains either by direct absorption or indirect absorption (e.g. photolytic heating). The evaporated water will be photolysed and yield OH with a peculiar nascent distribution over different quantum states. The continued formation and relaxation yields inversion between all those quantum states between which masing has been observed in star forming regions. The OH quantum state distribution presented here might also be affected by the absorption of FIR radiation from the surrounding dust and the reabsorption of the OH rotational lines which are emitted after photolysis of water because OH is formed in rotationally excited states. Because of the difficulties in quantifying these effects, they are excluded up to now. Nevertheless we think that the photodissociation and the subsequent IR relaxation will dominate the quantum state population at least under certain conditions, e.g. at high photodissociation rates. For the ground state masers the FIR pumping may play a more important role than for the excited state masers.
The evaporation from the grains is described by the evaporation rate ![]() , i.e., the
number of
water molecules desorbed from grains per
, i.e., the
number of
water molecules desorbed from grains per ![]() and second. In the evaporation process
water
molecules go off the grains to the gas phase, which implies that the grain size decreases with
time.
and second. In the evaporation process
water
molecules go off the grains to the gas phase, which implies that the grain size decreases with
time.
In the gas phase the water molecules are photolysed in the VUV radiation field with a
photodissociation rate ![]() . The nascent OH is formed in different quantum states
with a
probability fi for state i. The nascent quantum state population in OH relaxes subsequently
by
IR emission towards lower states with IR relaxation rates Aik. There is an interesting
competition
between photodissociation and IR relaxation which depends on the photodissociation rate. The
OH is also photolysed in the VUV radiation field with a photodissociation rate
. The nascent OH is formed in different quantum states
with a
probability fi for state i. The nascent quantum state population in OH relaxes subsequently
by
IR emission towards lower states with IR relaxation rates Aik. There is an interesting
competition
between photodissociation and IR relaxation which depends on the photodissociation rate. The
OH is also photolysed in the VUV radiation field with a photodissociation rate ![]() ,
which presents
the only loss mechanism for ground state OH in the present model. The corresponding maser
model is shown in Fig. 2.
,
which presents
the only loss mechanism for ground state OH in the present model. The corresponding maser
model is shown in Fig. 2.
The density of the grains with radius ![]() (number of grains of that radius per
(number of grains of that radius per ![]() ) is
denoted by
) is
denoted by
![]() . From the number
. From the number ![]() of grains with radius
of grains with radius ![]() and
their surface
and
their surface ![]() we calculate
the grain surface area contained in
we calculate
the grain surface area contained in ![]() of the maser volume by
of the maser volume by ![]() .
.![]() is thus the total surface (= the sum of the surfaces of all grains) contained in
is thus the total surface (= the sum of the surfaces of all grains) contained in ![]() with the unit
with the unit ![]() .
.
The number of molecules desorbed per area and second, i.e. the desorption flux density
![]() , multiplied with the surface area
, multiplied with the surface area ![]() per
per ![]() yields the evaporation rate
yields the evaporation rate
![]()
| |
(1) |
![\begin{displaymath}
\frac{{\rm d}}{{\rm d} t}
{\rm [H_2O]}=+\Gamma - \gamma_1 \cdot {\rm [H_2O]},\end{displaymath}](/articles/aas/full/1999/11/h1151/img28.gif) |
(2) |
| |
(3) |
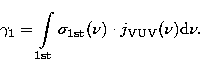 |
(4) |
Each photodissociation event leads to an OH molecule. Thus the density [OH] of OH
increases due to the photodissociation of water by ![]() . Simultaneously the OH
density
decreases due to the photodissociation of OH by
. Simultaneously the OH
density
decreases due to the photodissociation of OH by ![]() [OH].
[OH].
![\begin{displaymath}
\frac {{\rm d}}{{\rm d}t}{\rm [OH]}=+\gamma_1
{\rm [H_2O]} - \gamma_2{\rm [OH]}.\end{displaymath}](/articles/aas/full/1999/11/h1151/img43.gif) |
(5) |
![\begin{displaymath}
{\rm [OH]}=\frac{\Gamma}{\gamma_2}\cdot\end{displaymath}](/articles/aas/full/1999/11/h1151/img45.gif) |
(6) |
Now we show that the water evaporated from grains attenuates the VUV field not too much.
The optical density for the absorption of VUV in the first absorption band of water is given by
![]() , where the average absorption cross section is
, where the average absorption cross section is ![]() . The density of water under stationary conditions is determined
according to Eq. (2) by
. The density of water under stationary conditions is determined
according to Eq. (2) by ![]() . With a high evaporation rate of
. With a high evaporation rate of
![]() and
and ![]() , which we will consider as an extreme
case only for the j=7/2 masers, we obtain
, which we will consider as an extreme
case only for the j=7/2 masers, we obtain ![]() . Even for this upper limit, the
optical density is lower than
. Even for this upper limit, the
optical density is lower than ![]() which implies that the VUV field can
penetrate 1000 AUs deep into the maser volume. Close to the border of
the HII region the
attenuation of the VUV by evaporating water is therefore negligible.
which implies that the VUV field can
penetrate 1000 AUs deep into the maser volume. Close to the border of
the HII region the
attenuation of the VUV by evaporating water is therefore negligible.
A warning should be given here because the simplistic picture given above does not hold in
detail. The state to state photodissociation yields in some cases even anti-inversion between
the ![]() -doublets. In addition vibrational excitation can not be neglected. An even more
detailed study about the wavelength dependent nascent OH quantum state distribution from
single
-doublets. In addition vibrational excitation can not be neglected. An even more
detailed study about the wavelength dependent nascent OH quantum state distribution from
single ![]() quantum states is required to improve the present model.
quantum states is required to improve the present model.
![\begin{figure}
\begin{center}
\includegraphics [width=7cm,clip]{1151f3.eps}
\end{center} \end{figure}](/articles/aas/full/1999/11/h1151/Timg61.gif) |
Figure 3:
Nascent OH population out of photodissociation of water as a fraction of the total
number of dissociated molecules. In equilibrium with OH photolysis the population is given as
|
The derived values of fi are shown in Fig. 3.
The nascent population can be calculated from the fi values. In the stationary case
Eqs. (2) and (5) vanish. This gives:
 |
(7) |
The reader may be reminded that the total OH density is simply the sum over the OH quantum state populations (compare Eq. (6)).
We will demonstrate that by far the largest population - and therefore the highest gain - is obtained in the ground states for small photodissociation rates. The result that the highest gain is obtained for low photodissociation rates may be surprising at the first glance but becomes obvious in the following discussion.
The density ni in quantum state i of OH increases due to photodissociation of water by
![]() and decreases due to photodissociation of OH by
and decreases due to photodissociation of OH by ![]() . In
addition, the quantum state
density decreases because of IR relaxation out of state i to lower states by
. In
addition, the quantum state
density decreases because of IR relaxation out of state i to lower states by ![]() , where the
sum goes over all final states that can be reached from state i and increases because of IR
relaxation from higher states by
, where the
sum goes over all final states that can be reached from state i and increases because of IR
relaxation from higher states by ![]() . This implies
. This implies
![\begin{displaymath}
\frac{{\rm d}}{{\rm d}t}n_i=+f_i\gamma_1 {\rm [H_2O]} - \gamma_2 n_i -\sum\limits_{k} A_{ik}
n_i+\sum\limits_{k} A_{ki} n_k.\end{displaymath}](/articles/aas/full/1999/11/h1151/img69.gif) |
(8) |
The equation system is solved numerically. For this we rewrite
Eq. (8) as a matrix equation. We define a vector n by ![]() representing the density of OH
in different quantum states and a vector f by
representing the density of OH
in different quantum states and a vector f by ![]() containing the
probabilities for the
formation of OH in different quantum states as described in
Sect. 2.1. We define
further a diagonal matrix D with
matrix elements (dij) with
containing the
probabilities for the
formation of OH in different quantum states as described in
Sect. 2.1. We define
further a diagonal matrix D with
matrix elements (dij) with ![]() which account
for the IR relaxation out of state i and a
matrix A with only off diagonal elements Aki which accounts for the IR relaxation
into state i
from all states k that are above state i and are possible due to the IR selection rules. The
matrices contain
which account
for the IR relaxation out of state i and a
matrix A with only off diagonal elements Aki which accounts for the IR relaxation
into state i
from all states k that are above state i and are possible due to the IR selection rules. The
matrices contain ![]() elements.
With these definitions we rewrite
Eq. (8):
elements.
With these definitions we rewrite
Eq. (8):
![\begin{displaymath}
\frac{{\rm d}}{{\rm d}t} {\vec n}\!=\!
{\vec f}\gamma_1 {\rm...
...
{\vec f}\gamma_1 {\rm [H_2O]} \!+\!
{\bf T(\gamma_2)}{\vec n}\end{displaymath}](/articles/aas/full/1999/11/h1151/img76.gif) |
(9) |
For a stationary maser all time derivatives in
Eqs. (2, 5, 8, 9, 12, 13) vanish. In particular we have
![]() and obtain the quantum state densities from the solution of the matrix
Eq. (15)
and obtain the quantum state densities from the solution of the matrix
Eq. (15)
| |
(10) |
Figure 4 shows how the OH quantum state populations are affected by the competition
between photodissociation and IR relaxation. The population is given here only for the four
lowest rotational states of the ![]() ladder resolved according to hyperfine structure. An
absolute value of
ladder resolved according to hyperfine structure. An
absolute value of ![]() is used here for the evaporation rate which
determines the total OH density but has no effect on the OH quantum state distribution.
is used here for the evaporation rate which
determines the total OH density but has no effect on the OH quantum state distribution.
The nascent OH population resulting directly from photodissociation of ![]() is given
in both plots (filled bars) to allow an easier comparison with the OH populations resulting from
our maser model (open bars) which includes the competition between photodissociation and IR
relaxation. The only difference between the two figures is that a
is given
in both plots (filled bars) to allow an easier comparison with the OH populations resulting from
our maser model (open bars) which includes the competition between photodissociation and IR
relaxation. The only difference between the two figures is that a
![]() smaller photodissociation
rate is used in Fig. 4A. The actual value of the photodissociation rates is given in the
corresponding figure.
smaller photodissociation
rate is used in Fig. 4A. The actual value of the photodissociation rates is given in the
corresponding figure.
The first and most obvious difference between Figs. 4A
and 4B is that more than an order of
magnitude larger total OH densities are obtained for the smaller photodissociation rate. The
population in Fig. 4A goes up to more than ![]() whereas it stays at several times
whereas it stays at several times
![]() in Fig. 4B. This somewhat surprising result is easily
understood in terms of
Eq. (6),
which predicts for a
in Fig. 4B. This somewhat surprising result is easily
understood in terms of
Eq. (6),
which predicts for a ![]() larger destruction rate of OH,
larger destruction rate of OH, ![]() less total OH. It may be emphasized
again that the same evaporation rate is used in both cases. The very large population in the
ground state of more than
less total OH. It may be emphasized
again that the same evaporation rate is used in both cases. The very large population in the
ground state of more than ![]() leads to large inversion and gain for the ground state
masers for low photodissociation rates.
leads to large inversion and gain for the ground state
masers for low photodissociation rates.
Large differences are also found for the relative distribution among the quantum states. Obviously the nascent distribution differs considerably from that of our maser model. Because IR relaxation transfers population from higher to lower states the distribution obtained from our model is always shifted towards lower states compared to the nascent distribution. This shift is more pronounced for small photodissociation rates because the OH molecules have more time to relax before they are destroyed by photodissociation.
For the small photodissociation rates almost all population is concentrated in the ground state
with little population left in excited states. For the high photodissociation rate ![]() in Fig. 4B there is still more population in the ground state than in higher states. In
comparison to the small photodissociation rate there is relatively more population in the first
excited state (j=5/2) and also the j=7/2 state has a non-vanishing population. The excited
states are populated more, because at higher dissociation rate (such as 0.2/s) the OH molecules
have less time to relax before they are destroyed.
in Fig. 4B there is still more population in the ground state than in higher states. In
comparison to the small photodissociation rate there is relatively more population in the first
excited state (j=5/2) and also the j=7/2 state has a non-vanishing population. The excited
states are populated more, because at higher dissociation rate (such as 0.2/s) the OH molecules
have less time to relax before they are destroyed.
It may be interesting to note that the population of the first excited state
(j=5/2) is enhanced
compared to the nascent population. This is because the IR relaxation out of this state is
slower than the IR relaxation into this state. Our results show an enhancement of the
population in a given quantum state - relative to the nascent population - as long as the
photodissociation rate ![]() exceeds the IR relaxation rate
exceeds the IR relaxation rate ![]() of this particular
rotational state (e.g.
of this particular
rotational state (e.g. ![]() ,
, ![]() ,
,
![]() ).
).
In order to evaluate the influence of the photodissociation rate in a more detailed way the population inversion for some important OH maser transitions is plotted in Fig. 5. The population inversion PIul is defined as the difference between the population of the upper level (nu) and the population of the lower level (nl):
| PIul=nu-nl. | (11) |
The inversion in the excited states behaves in a very different manner than the inversion in the ground state. Whereas the inversion in the ground state increases dramatically with decreasing dissociation rates it remains almost constant for the excited states for small dissociation rates and drops off only at larger dissociation rates. This effect was already discussed above but becomes more obvious here. This effect is understood in terms of the different losses out of the ground and excited states: losses due to IR relaxation occur only out of the excited states whereas there is no such loss out of the ground state. Because the only loss in the ground state results from destruction of OH by photodissociation these losses decrease with decreasing dissociation rate.
For the excited states the loss rate is dominated by the losses due to IR relaxation, which is
independent of ![]() . This leads to an almost constant population inversion for low
dissociation rates, which is, however, much smaller than in the ground state. Only at
dissociation rates higher than 0.1/s the losses due to photodissociation become comparable to
the losses due to the IR relaxation. This causes the population and therefore the population
inversion to go down. This bend-off is weaker for the higher excited states than for the lower
lying excited states and the ground state.
. This leads to an almost constant population inversion for low
dissociation rates, which is, however, much smaller than in the ground state. Only at
dissociation rates higher than 0.1/s the losses due to photodissociation become comparable to
the losses due to the IR relaxation. This causes the population and therefore the population
inversion to go down. This bend-off is weaker for the higher excited states than for the lower
lying excited states and the ground state.
It may be interesting to note that for higher ![]() 's (
's (![]() ) the population inversion
becomes higher in the excited states than for the ground states.
) the population inversion
becomes higher in the excited states than for the ground states.
The ![]() densities are not expected to exceed
densities are not expected to exceed ![]() . This
yields a collisional
probability
. This
yields a collisional
probability ![]() . According to the discussion above, the
photodissociation rates are expected to vary between
. According to the discussion above, the
photodissociation rates are expected to vary between ![]() and 1/s. This implies that
collisions will affect the OH quantum state densities only for small photodissociation
rates.
and 1/s. This implies that
collisions will affect the OH quantum state densities only for small photodissociation
rates.
Because the IR relaxation from excited states is fast, the excited state OH masers have to be
pumped fast to
compete with IR relaxation. We assume that at least for the case of the 13441 MHz
(j=7/2) with relaxation rates of ![]() collisions can be neglected safely. Even
effects like FIR pumping will play a minor role so that the present model is expected to hold
better for the excited state masers.
collisions can be neglected safely. Even
effects like FIR pumping will play a minor role so that the present model is expected to hold
better for the excited state masers.
 |
If the lower and upper maser level are denoted by l and u,
respectively, we
obtain:
![\begin{displaymath}
\frac{{\rm d}}{{\rm d}t}n_l=+f_i\gamma_1 {\rm [H_2O]} - \gamma_2 n_l -\sum\limits_{k} A_{lk} n_l+S_{ul}
n_l-S_{ul}n_u
\\ \end{displaymath}](/articles/aas/full/1999/11/h1151/img108.gif) |
(12) |
![\begin{displaymath}
\frac{{\rm d}}{{\rm d}t}n_u=+f_i\gamma_1 {\rm [H_2O]} - \gamma_2 n_i -\sum\limits_{k} A_{uk} n_u-
S_{ul}n_u+S_{ul}n_l\end{displaymath}](/articles/aas/full/1999/11/h1151/img109.gif) |
(13) |
| |
(14) |
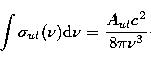 |
(15) |
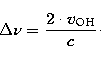 |
(16) |
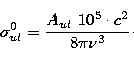 |
(17) |
| (18) |
For the amplification of the photon flux along some propagation direction
z we use the peak
cross section for
stimulated emission and obtain:
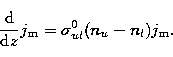 |
(19) |
| |
(20) |
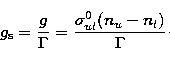 |
(21) |
![\begin{figure}
\includegraphics [width=7cm,clip]{1151f6a.eps}
\includegraphics [width=7cm,clip]{1151f6b.eps}
\end{figure}](/articles/aas/full/1999/11/h1151/Timg129.gif) |
Figure 6:
The specific gain calculated from our model for all maser transitions observed in
W3(OH).
The absolute gain can be
derived by multiplying the specific gain with the
evaporation rate |
Figure 6A shows the specific gain for the maser transitions in the ![]() ladder as
a function of the photodissociation rate
ladder as
a function of the photodissociation rate ![]() . In general, the results for the specific gain
are similar to those for the population inversion that was shown in
Fig. 5. This is not
surprising because, apart from the evaporation rate, the only important difference between
specific gain and population inversion is the different cross section for stimulated emission
(compare Eq. (20)). The comparison between Figs. 5 and 6 thus shows the effects resulting from
the different cross sections for stimulated emission. The general agreement in features, like
increase of the specific gain in the ground state with decreasing
. In general, the results for the specific gain
are similar to those for the population inversion that was shown in
Fig. 5. This is not
surprising because, apart from the evaporation rate, the only important difference between
specific gain and population inversion is the different cross section for stimulated emission
(compare Eq. (20)). The comparison between Figs. 5 and 6 thus shows the effects resulting from
the different cross sections for stimulated emission. The general agreement in features, like
increase of the specific gain in the ground state with decreasing ![]() or the bend-over for
the excited state at larger dissociation rates are therefore easily understood.
or the bend-over for
the excited state at larger dissociation rates are therefore easily understood.
A large difference appears between specific gain and inversion for the main and satellite lines in
the ground state. The specific gain for the 1612 MHz and 1720 MHz masers is much smaller
than for the 1667 MHz and 1665 MHz masers although the inversion is similar. This is a result
of the roughly ![]() smaller stimulation cross section
smaller stimulation cross section ![]() for the satellite lines
compared to the main lines.
for the satellite lines
compared to the main lines.
For the excited states the specific gain is again almost constant over a wide range of
![]() 's and decreases when the photodissociation rate becomes as large as the IR
relaxation rate. Because the stimulation rates are smaller for the excited states the specific
gain - in contrast to the population inversion - is always smaller in the excited states than for
the ground state main line transitions.
's and decreases when the photodissociation rate becomes as large as the IR
relaxation rate. Because the stimulation rates are smaller for the excited states the specific
gain - in contrast to the population inversion - is always smaller in the excited states than for
the ground state main line transitions.
This seems to propose that ground state masers should dominate excited state masers even at high dissociation rates. Such conclusions cannot be drawn. First, it is not clear how the much larger spontaneous emission rates in the excited states compared to the ground state affect the appearance of a given maser transition.
Second, if the dissociation rates become larger than the IR relaxation rates, the population
distribution for both the ground and excited states approaches the nascent population from
direct photolysis. The nascent inversion in the ground state, however, depends strongly on the
population of quantum states in the parent water molecule ([Häusler et al.] 1987). Photodissociation of the
rotational ground state of water even
yields anti-inversion for the ground state transitions in
OH. For small dissociation rates this effect is less important because the high nascent inversion
in the high lying rotational states is transferred to the ground state. This is because the IR
relaxation conserves the inversion. Consequently the model given above is too simple for the
ground state at large dissociation rates. A closer look at this problem reveals that for high
![]() 's the picture will change but remain more or less constant for low
's the picture will change but remain more or less constant for low ![]() 's,
because the population inversion is then more determined by IR relaxation from highly inverted
upper rotational states.
's,
because the population inversion is then more determined by IR relaxation from highly inverted
upper rotational states.
Figure 6B shows the specific gain for the three transitions of the ![]() state. Photodissociation of
state. Photodissociation of ![]() yields anti-inversion between all
yields anti-inversion between all ![]() -doublets
of the
-doublets
of the ![]() multiplet and therefore yields a "negative specific gain" as seen for the
4750 MHz and the 4660 MHz transitions in Fig. 6B. For the 4765 MHz transition,
however, a different behavior is observed. Here the specific gain is still negative for small
dissociation rates below 0.05/s as expected. However, for
multiplet and therefore yields a "negative specific gain" as seen for the
4750 MHz and the 4660 MHz transitions in Fig. 6B. For the 4765 MHz transition,
however, a different behavior is observed. Here the specific gain is still negative for small
dissociation rates below 0.05/s as expected. However, for ![]()
![]() the specific
gain becomes positive with a maximum of
the specific
gain becomes positive with a maximum of
![]() at
at ![]() . Nevertheless the specific gain stays small and it may be hard
to explain this maser without additional mechanisms like FIR pumping.
. Nevertheless the specific gain stays small and it may be hard
to explain this maser without additional mechanisms like FIR pumping.
The gain g is obtained from the specific gain ![]() by multiplication with
by multiplication with ![]() . It will be
seen below
that
. It will be
seen below
that ![]() can vary strongly with the astrophysical conditions and depends sensitively on
the density, sizes and temperatures of the grains. This implies in turn a large variation of maser
phenomena with different astrophysical conditions.
can vary strongly with the astrophysical conditions and depends sensitively on
the density, sizes and temperatures of the grains. This implies in turn a large variation of maser
phenomena with different astrophysical conditions.
The calculations given below neglect saturation effects which implies exponential
growth of the maser intensity and yields for an amplification factor ![]()
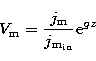 |
(22) |
In Fig. 6 it can be seen that the specific gain in the j=3/2 maser can become very large,
in particular for dissociation rates lower than ![]() . Under these circumstances
population and inversion are accumulated in the ground state due to IR-relaxation with little
OH destroyed by photodissociation. Note that the nascent inversion in the ground state is
lower than the inversion after relaxation.
. Under these circumstances
population and inversion are accumulated in the ground state due to IR-relaxation with little
OH destroyed by photodissociation. Note that the nascent inversion in the ground state is
lower than the inversion after relaxation.
This is illustrated by an example with a photodissociation rate of
![]() , where we obtain a specific gain of
, where we obtain a specific gain of ![]() for the 1667 MHz maser. A
moderate evaporation rate of
for the 1667 MHz maser. A
moderate evaporation rate of ![]() yields a gain of
yields a gain of
![]() , which implies under the
assumption of exponential growth an amplification of
, which implies under the
assumption of exponential growth an amplification of ![]() for a tube length of
roughly 150 AU. For the 6035 MHz maser the specific gain is
for a tube length of
roughly 150 AU. For the 6035 MHz maser the specific gain is ![]() for
for ![]() below
0.1/s. Nevertheless, a gain of
below
0.1/s. Nevertheless, a gain of ![]() can be obtained, with a
much higher
evaporation rate of
can be obtained, with a
much higher
evaporation rate of ![]() , however. In this case an amplification of
106 is obtained with a tube length of roughly 60 AU.
, however. In this case an amplification of
106 is obtained with a tube length of roughly 60 AU.
For the 13.44 GHz maser the specific gain is even smaller. In the range of low
photodissociation rates we have ![]() . To explain the gain of
. To explain the gain of
![]() , suggested by [Baudry & Diamond] (1998) for the single bright maser spot in W3(OH), an even higher
evaporation rate of
, suggested by [Baudry & Diamond] (1998) for the single bright maser spot in W3(OH), an even higher
evaporation rate of
![]() is required. This gain yields an amplification of
is required. This gain yields an amplification of
![]() for a tube length of 15 AU. It should be mentioned that there is a general
background of 20 mJy at the maser frequency from all over the region of this maser. The
amplification of this background by
for a tube length of 15 AU. It should be mentioned that there is a general
background of 20 mJy at the maser frequency from all over the region of this maser. The
amplification of this background by ![]() yields exactly the 20 Jy observed for the
single bright maser spot.
yields exactly the 20 Jy observed for the
single bright maser spot.
For the 4765 MHz maser in ![]() state gain is obtained only for
photodissociation rates
above 0.05/s. The maximum specific gain is obtained for
state gain is obtained only for
photodissociation rates
above 0.05/s. The maximum specific gain is obtained for ![]() and is
there around
and is
there around ![]() ,
the smallest specific gain from all observed masers. Even with
,
the smallest specific gain from all observed masers. Even with ![]() we obtain a gain of
only
we obtain a gain of
only ![]() and require a tube length of 50 AU for an amplification of 1000. This
maser
operates according to the present model only if the photodissociation and the evaporation
rates are high.
and require a tube length of 50 AU for an amplification of 1000. This
maser
operates according to the present model only if the photodissociation and the evaporation
rates are high.
To summarize the results from our gain considerations, we state that over a wide range of
![]() 's
specific gain is obtained for all observed maser transitions that appear in regions of star
formation. In contrast to the specific gain, the gain itself depends strongly upon the
evaporation rates. For the same evaporation rate the relative gain between different states is
determined by the relative specific gains. The specific gain for the excited state masers in
's
specific gain is obtained for all observed maser transitions that appear in regions of star
formation. In contrast to the specific gain, the gain itself depends strongly upon the
evaporation rates. For the same evaporation rate the relative gain between different states is
determined by the relative specific gains. The specific gain for the excited state masers in
![]() is much smaller than for the ground state masers. Small specific gain is obtained also for the
4765 MHz maser, however, only for
is much smaller than for the ground state masers. Small specific gain is obtained also for the
4765 MHz maser, however, only for ![]() above 0.05/s. Much smaller specific gain is
also obtained between states higher than j=7/2 in
above 0.05/s. Much smaller specific gain is
also obtained between states higher than j=7/2 in ![]() where no masing is observed.
However, the gain is so small for these states that masing is not expected from the present
maser model, in agreement with observations.
where no masing is observed.
However, the gain is so small for these states that masing is not expected from the present
maser model, in agreement with observations.
For all states in ![]() the gain for the F state with higher multiplicity dominates the
gain with
lower multiplicity. This predicts a preference for hyperfine transitions in the sense that the
transition belonging to the larger F- value should be stronger. For the ground state masers the
gain for the main lines dominates that for satellite lines. Because the specific gain can become
very high in the ground state the satellite lines are also expected to yield maser radiation with a
slight preference for the 1720 MHz transition.
the gain for the F state with higher multiplicity dominates the
gain with
lower multiplicity. This predicts a preference for hyperfine transitions in the sense that the
transition belonging to the larger F- value should be stronger. For the ground state masers the
gain for the main lines dominates that for satellite lines. Because the specific gain can become
very high in the ground state the satellite lines are also expected to yield maser radiation with a
slight preference for the 1720 MHz transition.
Here we discuss whether spontaneous emission from a tubular volume with cross
sectional area ![]() and length l can start the maser even without external background
emission from
e.g. grains. We use the quantum state populations given in Sect. 2.2. We consider an
infinitesimal
element
and length l can start the maser even without external background
emission from
e.g. grains. We use the quantum state populations given in Sect. 2.2. We consider an
infinitesimal
element ![]() along the maser's propagation direction z which has a volume
along the maser's propagation direction z which has a volume
![]() with a
density nu in the upper maser level. The number of spontaneous emission events from this
volume is
with a
density nu in the upper maser level. The number of spontaneous emission events from this
volume is ![]() per second. The fraction
per second. The fraction ![]() of these spontaneous photons
passes through the exit area of the maser tube. Only these spontaneous photons will propagate
through the inverted maser volume, will be amplified on this path and contribute to the maser
emission observed on earth. The maser photon flux density that exits the front area
of these spontaneous photons
passes through the exit area of the maser tube. Only these spontaneous photons will propagate
through the inverted maser volume, will be amplified on this path and contribute to the maser
emission observed on earth. The maser photon flux density that exits the front area ![]() of the
maser tube is then
of the
maser tube is then ![]() .
The maser flux density will give rise also to the stimulated emission
.
The maser flux density will give rise also to the stimulated emission ![]() in
the volume
in
the volume ![]() . The increase
. The increase ![]() of the maser flux density results therefore not only
from the spontaneous emission
of the maser flux density results therefore not only
from the spontaneous emission ![]() but also from the
stimulated emission
but also from the
stimulated emission ![]() which implies
which implies
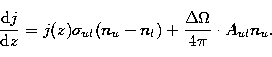 |
(23) |
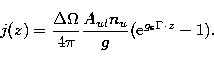 |
(24) |
In contrast, the ground state satellite line masers and the excited state maser show a much
smaller growth under these conditions that are chosen to explain the main line ground state
masers. This results from their much smaller specific gain which in turn comes from the small
evaporation rate of only ![]() . This implies the main line ground state
masers will work even far away from the star, whereas the excited state masers will not
operate there.
According to the discussion below much higher evaporation rates may be expected closer to
the star. There the specific gains of the different maser transitions becomes more similar at the
expected higher dissociation rates (see Fig. 6). The competition between the masers
under these conditions (closer to the star) have not been investigated yet.
. This implies the main line ground state
masers will work even far away from the star, whereas the excited state masers will not
operate there.
According to the discussion below much higher evaporation rates may be expected closer to
the star. There the specific gains of the different maser transitions becomes more similar at the
expected higher dissociation rates (see Fig. 6). The competition between the masers
under these conditions (closer to the star) have not been investigated yet.
Nevertheless the results show that with reasonable tube length the ground state maser may start with spontaneous emission without any amplification of background radiation from the surrounding dust shell. At a given maser tube length the output becomes higher with such additional microwave background radiation.
Copyright The European Southern Observatory (ESO)