8 Mass and age of dwarf A0 stars

8.1 The HR diagram

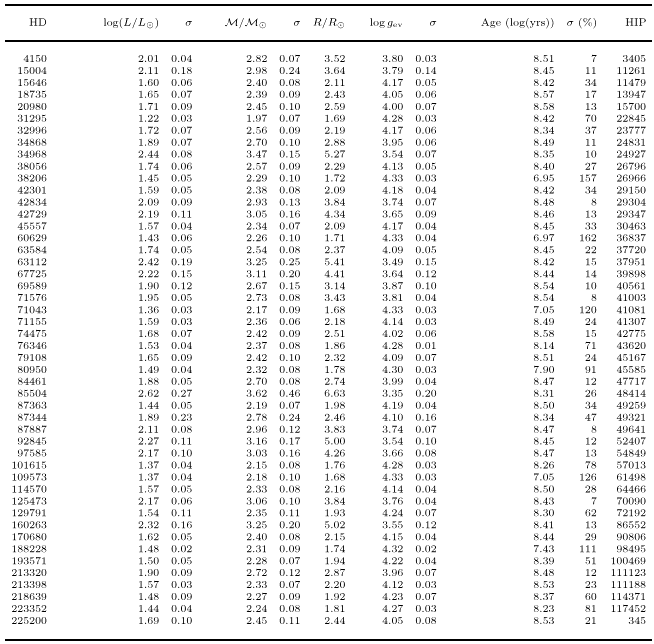
Hipparcos parallaxes enable us to establish the HR diagram for this set of stars, in order to determine their masses and ages.

The effective temperature is that derived from photometric calibrations. The visual absolute magnitudes (M_V) and their ${\sigma}$ are computed from the parallax data taken from the Hipparcos Main Catalogue and given in Cols. 13, 14 and 15, 16 of Table 2. These values are obtained by taking into account the colour excess.

One of our goals being to compute the stellar masses, we restrict the analysis to the reduced sample defined in the previous section.

We create the HR diagram by plotting the $T_{\mathrm{eff}}$ derived from the MD calibration versus the luminosity (Fig. 9). The luminosity has been computed from M_V with a bolometric correction taken from the Bessell et al. (1998) tables and $M_{\rm bol\odot}=4.75$, as given by Cayrel de Strobel (1996), and adopted by IAU Commissions 29 and 36 (1997, IAU General Assembly). The values of $L/L_{\odot}$ are given in Table 4, Col. 2 and the errors in Col. 3; these latters are due to the errors on the parallaxes. On this plot the stars are divided according to their photometrically derived logg(MD) values. The evolutionary tracks by Schaller et al. (1992) are overplotted for 2.0, 2.5 and 3.0 solar masses, and Z=0.02.

  

Table 4: Parameters computed from the HR diagram and evolutionary tracks for the reduced sample; the star HD 216931 has been excluded from this table as well as HD 27660. The evolutionary tracks used for these computations are those by Schaller et al. (1990). The errors are given for the determination of log$(L/L_\odot$), $\cal M$/$\cal M$$_\odot$, log$g_{\rm ev}$. For the ages the error is given in percentage

The cross represents the Vega position ($T_{\mathrm{eff}}=$ 9550 K; log g=3.95 according to Castelli & Kurucz (1994). The position of the misclassified HD 216931 lies out of the boundaries of the plot.

  

Figure 9: The HR diagram for the reduced sample. The luminosity is expressed in $L/L_{\odot}$.The logg ranges are distinguished by using the following symbols: $\ast$ logg ${\geq}$ 4.3; $\triangle$ 4.05 ${\leq}$ logg <4.3; + 3.8 < logg < 4.05; hexagone logg ${\leq}$ 3.8; The filled symbols triangle and hexagone are used for the evolutionary tracks with the same intervals for logg. Vega is labelled with the symbol: $\times$

We note the large spread in luminosity; we note also that Vega parameters do not represent the average values of dwarf A0 stars neither in luminosity nor in $T_{\mathrm{eff}}$.

We remark that the only non peculiar A0 III star of our sample (HD 87887) does not have the lowest logg value (3.55), nor the brightest luminosity (log($L/L_{\odot}) = 2.11$). If we do not consider the shell stars, the most extreme values, which should indicate the most luminous objects, are the lowest value of logg = 3.30 (HD 67725) or the largest value for log($L/L_{\odot}$) (2.62) (HD 85504); we note that both refer to stars classified as A0 V.

We recall that HD 67725 (log($L/L_{\odot}) = 2.22$)is reddened and has an H$_\gamma$ profile which is not reproduced by computations. HD 85504 is a peculiar object which has the spectral properties of a Population I star and the kinematics of a Population II star, according to Adelman & Pintado (1997).

8.2 Evolutionary based surface gravity

We used the HR diagram to derive the value of log$g_{\rm ev}$ from evolutionary models and the Hipparcos parallaxes in order to compare them with the value of log$g_{\rm ph}$ obtained from photometric data.

Balona (1994) found serious discrepancies between the gravities derived from evolutionary models and those obtained from photometric and spectroscopic determinations; this author questioned the reliability of the photometrically derived logg values and of the Kurucz (1979) LTE grid of models.

To compute log$g_{\rm ev}$ ($g_{\rm ev}$ = G${\cal M} /R^{2}$), we applied the following relation:

$$R = (L/4{\pi}{\sigma}T_{\rm eff}^{4})^{1/2}$$

The stellar masses $\cal M$/$\cal M$$_\odot$ are derived from $L/L_{\odot}$and $T_{\mathrm{eff}}$ by interpolation using Asiain (1998) method on the same evolutionary tracks (Schaller et al. 1992) used in the previous sub-section. The results are given in Table 4 Col. 4 and Col. 5 for the errors; the mean value of the error on the mass determination, due to the uncertainty on M_V is 0.1 $\cal M/ \cal M_\odot$.

We compare these log$g_{\rm ev}$ (the values are given Table 4) with the log$g_{\rm ph}$ obtained from $ubvy\beta$ photometric data Fig. 10. The log$g_{\rm ph}$ have been already compared with model atmosphere calculations; our data include a Balmer line, which in this domain of temperature, is highly sensitive to the surface gravity. If we exclude the two shell stars (HD 15004, HD 225200) the most discrepent between the two logg determinations are for: HD 67725, HD 85504, HD 114570 whose peculiarities are discussed in the Appendix; for two more stars, HD 69589 and HD 87344, we do not have any obvious explanation.

From the diagram plotted Fig. 10 we note that, for most of the stars, the evolutionary gravities agree reasonably well with the photometric ones, the log$g_{\rm ev}$ being systematically slightly higher than the log $g_{\rm ph}$, except for the stars with logg ${\geq}$ 4.3. The behaviour of these "high" gravity stars is related to the systematic overestimation of logg by MD as discussed in Sect.4.

We cannot confirm, in our range of gravity values, the discrepancy found by Balona (1994), the discrepancy being, at least partly, due to the use of old Kurucz models and the Lester et al. (1986) synthetic indices.

  

Figure 10: The relation between (log $g)_{\rm ev}$ and (log $g)_{\rm ph}$; the latter is that derived from the MD calibration; the symbols are the same as in Fig. 9

8.3 Mass-luminosity relation

In order to evaluate the possible dependency of mass values with respect to the adopted stellar models, we compared the masses, as computed in the previous section, with those obtained by interpolating in the tracks by Bressan et al. (1993) and by Lebreton et al. (1997) using the CESAM code (Morel 1997). The differences between the masses computed from Schaller et al. (1992) and Bressan et al. (1993) have a mean value of -0.01 $\cal M$/$\cal M$$_\odot$ and for Lebreton computations, the differences have a mean value of 0.04 $\cal M$/$\cal M$$_\odot$, which is negligible for our analysis.

We underline the fact that through the Hipparcos experiment the $\cal M$-L relationship can be derived from non eclipsing field stars. This relation is illustrated in Fig. 11a. We note the very tight relationship between the two parameters, mass and luminosity, but we recall that they cannot be considered as being totally independent both relying upon M_V for their determination.

We have compared the relation derived from our sample of stars to the empirical one from binary systems (see Fig. 5 in Andersen 1991), also plotted in the same Fig. 11a. The general agreement appears clearly. Let us recall that our relation depends on stellar evolutionary models and that the relation based on eclipsing binaries is totally independent from a methodological point of view. Figure 11a shows that the gap around log ${\cal M}=0.5$ in the Andersen sample is filled by the present study.

  

Figure 11: a) The mass versus luminosity diagram for the stars of luminosity class V in our ($\times$) and Andersen (square) samples. b) Zoom of the previous plot centered around A0 stars; the symbols are the same as in Fig. 9

Andersen (1991) pointed out a significant scattering of the points around the mean relation and related it to age and chemical composition effects on luminosity. The evolutionary effect on the stars of our sample is revealed by the logg parameter. If we split the stars of our and Andersen samples (in the $T_{\mathrm{eff}}$ range covered by A0 V stars) in narrow intervals of log g (see Fig. 11b), the dominant effect on the scatter is clearly related to gravity, since the mean relation for each group is smooth and better defined.

The use of the $\cal M$-L relationship to determine the mass of individual dwarf stars requires the knowledge of logg, parameter decreasing with stellar age, even inside the stellar main sequence life as it can be seen Fig. 12 where the effect of evolution is emphasized by overplotting the values of mass and luminosity derived from evolutionary models. Only the points corresponding to the core hydrogen burning phase are displayed.

As a result the derived luminosity is directly related to the accuracy of the adopted logg value.

  

Figure 12: The combined mass versus luminosity diagrams (same symbols as in Fig. 11b) on which the evolution of the luminosity for various masses (taken from Schaller et al. 1992, tables) is overplotted using the same symbols but with thick lines

The masses extracted from an HR diagram $L-T_{\mathrm{eff}}$ coupled with evolutionary tracks does not need the knowledge of log g and allows to derive the mass of a star by taking into account its distance from the ZAMS. In this case the uncertainty on the mass depends on the reliability of the evolutionary tracks.

8.4 Ages

The ages of the non binary and non peculiar stars have been determined by interpolation through the evolutionary tracks in the HR diagram and are given in Col. 9 of Table 4, the errors are expressed in % in Col. 10.

There are 6 stars younger than 10⁸ years.

From Table 4 and the corresponding Fig. 9 we note that a small number of objects are very near the ZAMS and may still preserve signs of their recent formation as, for instance, an IR excess. We underline once more that a significant number of slightly evolved stars is present among the A0 stars of luminosity class V.

8.5 Rotational velocities

We should not forget that a third parameter can affect the position of a star in the HR diagram: the rotational velocity. Such influence has been largely analysed from a theoretical point of view and recently studied, for stars hotter than those of the present paper, by Brown & Verschueren (1997).

We overplotted the observed spectra, after correction for RV, on the appropriate synthetic spectrum; the rotation value introduced in the computed spectrum that better fits the observations, is given in Col. 12 of Table 2, independent of the detection of established or suspected binarity. For some stars two values are given in the Table, when the $v\,\sin\,i$ was very uncertain; for HD 111786 the two values represent the velocities of the two components of the binary system. For the fastest rotators only H$_\gamma$ and Mg II 4481 can be used for the comparison with computations.

We know that dwarf A-type stars are intrinsically fast rotators and generally characterized by mean-high values of $v\,\sin\,i$, with an average value not lower than 100 $\mathrm {km\, s^{-1}}$. Stars with projected rotational velocities much lower than this value deserve some attention.

An account of the unknown parameter ${\it i}$,a low $v\,\sin\,i$ value may indicate that the object under study belongs to a class of the CP stars, is a close binary or is a Blue Horizontal Branch Star. From our sample we note that, among the 34 slowly rotating stars, 20 belong to one of the above categories.

The detection of binaries from broad lined spectra is more delicate and difficult; the availability of several orders of echelle spectra and the study of the cross correlation between observed and computed spectra has been fundamental for this detection.

Four of the observed stars belong to the Catalogue of $v\,\sin\,i$ standard stars by Slettebak et al. (1975). These stars are: HD 4150, HD 71155, HD 125473 and HD 188228.