5 Meso-Nh outputs and performances

5.1 Simulation of the flow by the model

To generate optical turbulence it is necessary to have both a temperature gradient and a dynamic instability (Coulman et al. 1995). We analyze first the thermic and then the dynamic sources of turbulence related to the 16/5/93 night of the PARSCA93 campaign in order to give an explicit demonstration that the lee waves produced by the high mountain steps are correctly resolved by the model. The temporal evolution of the potential temperature over 4 hour simulation time is reported in Figs. 2a-c. High density isolines regions correspond to static stability and low density isolines are associated with static instability. The irregular isolines indicate the presence of gravity waves. The source of these waves is the steep chilean coast and the waves propagate in the interior region (quoted by two straight lines in Figs. 2a-c) of the atmosphere over Paranal mountain. This suggests that some optical turbulence over Paranal is generated far away over the chilean coast. Figure 3 shows a vertical section of the vertical wind fluctuations selected over 40 km along the east-west direction centered over Paranal mountain. The alternation of positive and negative values is a further proof of the presence of gravity waves. This particular structure of the isolines in the first 10 km attests the sensitivity of the model in this part of the atmosphere. In Fig. 4 we report profiles of the wind vertical fluctuations obtained after 30 minutes, 1 hour and 4 hours of simulation time. The vertical wave propagation is deduced from the temporal sequence of images. Values of the order of 1 m/s in the first 12 km suggest that the model is capable of representing this aspect of the atmospheric dynamics. Finally in Fig. 5 we show a vertical section of the turbulence kinetic energy produced by orographic effect not only at the ground but also at higher altitudes (8000 m). The mixing length, shown in Fig. 6, is strongly correlated to energy e.

  

Figure 2: Potential temperature east-west vertical sections across the Paranal mountain extended over 40 km with a resolution of 500 m. Meso-Nh outputs during the 16/5/93 night (PARSCA93 campaign) at different simulation times. After a) 0 hours b) 2 hour c) 4 hours

  

Figure 3: Vertical wind fluctuations east-west vertical section across Paranal mountain after 4 hours simulation time during the 16/5/93 night (PARSCA93 campaign). Negative values mean a wind direction towards the ground and positive towards the top of the atmosphere

  

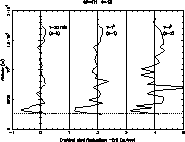Figure 4: Vertical wind fluctuations profile simulated above Paranal after 30 minute, 1 and 4 hours simulation time during the 16/5/93 night (PARSCA93 campaign)

  

Figure 5: Turbulent kinetic energy east-west vertical section across Paranal mountain after 4 hours simulation time during the 16/5/93 night (PARSCA93 campaign). The minimum value is 10-4 m/s-2

5.2 Simulation time to achieve a steady - state

Particular attention must be paid to define the simulation time necessary to adapt the flow to the orography and to converge to a steady state (spin-up time). We should expect that the adaptation time will, in general, depend on the initial configuration. In general, starting a simulation in a near dynamic equilibrium state will produce a faster adaptation process. In order to estimate this time we modified the code to have access to the temporal seeing evolution sampled with 2.5 s. Figure 7 shows the simulated temporal seeing evolution over Paranal related to the best and the worst PARSCA93 campaign nights with respect to the mean value of the whole campaign. During the 25/5/93 night (the best one), after about 1 hour, the seeing is oscillating around its mean value (0.7 arcsec). On the contrary, during the 16/5/93 night (the worst one) the seeing seems stable and, suddenly, increases to up 1.5 arcsec after 9 000 and 14 000 s, with a more chaotic trend. On this night, the strong degradation of the seeing is associated with the appearance of a turbulent layer at 4 km as one can see on the $C_{\rm N}^2$ profile Fig. 8. This turbulent layer is correlated to the gravity waves already shown in both potential temperature instabilities of Fig. 2 and vertical wind fluctuations Figs. 3 and 4). Moreover, in the same Fig. 8, the model reproduces the $C_{\rm N}^2$ profile measured by Scidar during the same night but, for this case, at least 4 hours are necessary to reproduce a correct vertical profile of turbulence spatial distribution.

  

Figure 6: As Fig. 5. Mixing length or also called geophysical outer scale

 

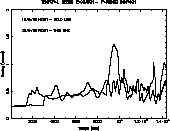Figure 7: Temporal seeing evolution (4 hours) during the 16/5 and the 25/5 nights (PARSCA93 campaign)

 

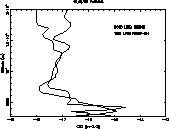Figure 8: $C_{\rm N}^2$ vertical profile above Paranal mountain simulated by Meso-Nh after 4 hours simulation time (thin line) and measured by Scidar (bold line) between 01:00 and 02:00 U.T. the 16/5/93 night

5.3 Sensitivity of results to horizontal resolution

A previous study (Bougeault et al. 1995) shows that the horizontal model resolution is, potentially, a critical parameter for the simulations. Two cases were studied (Bougeault 1995) using an horizontal resolution of 10 km (Lannemezan, altitude: 600 m) and 3 km (Mt. Lachens, altitude: 1700 m). In this last case, comparing the measured and simulated seeing at different grid points, the best spatial correlation was found at about 9 km beside the mountain peak. In the conclusion the authors ascribed the low spatial correlation to the poor horizontal resolution.

Using our model, having an horizontal resolution of 500 m, we can expect to obtain more precise results, resolving the development of the turbulence generated by dynamic instabilities, that is by gravity waves. To study the impact that the horizontal resolution could have on the simulations we used different resolutions on the same geographic surface. Sampling the ground surface on grid meshes of different dimensions, we could change the model resolution and we created further orographic maps having a lower resolution. The larger the grid dimension, the greater the average action of the model and the filtered energy. Figure 9 shows, as an example, the temporal seeing evolution over 4 hour simulation time for the 16/5/93 night of the PARSCA93 campaign obtained using horizontal resolutions of 1000 m and of 500 m. With the higher resolution configuration, the seeing fluctuations related to the $C_{\rm N}^2$ layers produced during the night at different altitudes are enhanced. This shows that the horizontal grid model dimension is a critical parameter for an operational model.

 

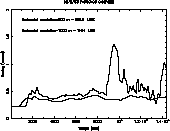Figure 9: Temporal seeing evolution during the 16/5/93 night simulated by Meso-Nh using two different horizontal resolutions: 1000 m $\times$ 1000 m (thin line) and 500 m $\times$ 500 m (bold line)

5.4 Model output relevant to astronomy

In the following, typical model outputs related to the same 16/5/93 night of the PARSCA93 campaign show how the simulation results could be useful for flexible scheduling and site testing.

In Fig. 10 is reported an east-west $C_{\rm N}^2$(x, z) vertical section centered on the Paranal and extending over 80 grid points (40 km). In Figs. 11a-e are reported east-west vertical sections, selected over the same 40 km, of different integrated parameters such as the seeing $\varepsilon$(Fig. 11a), the coherence wavefront time $\tau_{\rm AO}$ (Fig. 11b), the isoplanatic angle $\theta_{\rm AO}$(Fig. 11c), the scintillation rate $\sigma ^{2}_{\rm I}$ (Fig. 11d) and the spatial coherence outer scale ${\cal L}_0$(Fig. 11e). In Figs. 12a-e are displayed horizontal maps of the same parameters over the geographic surface displayed in (Fig. 1). One can observe the general coherence of these model outputs. Above the chilean coast, on the west, we find large seeing values as seen in Fig. 11a and Fig. 12a. This is caused by the presence of the steep slope of this mountainous region producing the maximum rate of turbulence. Weak seeing values characterize the central region around Paranal and, finally, a more important seeing is found above higher mountains (> 3000 m) east of Paranal.

 

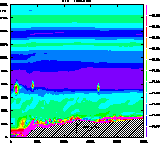Figure 10: 16/5/93 night (PARSCA93 campaign). $C_{\rm N}^2$ east-west vertical section across Paranal selected over the same surface as Fig. 2. Colour figure on Web A&AS site

 

Figure 11: As Fig. 10. East-west vertical sections of the integrated astronomic parameters coded in Meso-Nh model. a) Seeing $\varepsilon$. b) Coherence wavefront time $\tau_{\rm AO}$. c) Isoplanatic angle $\theta_{\rm AO}$. d) Scintillation rate $\sigma ^{2}_{\rm I}$. e) Spatial coherence outer scale ${\cal L}_0$. Paranal is located in the center of the vertical coupe. The chilean coast is placed at the 12-th grid point

  

Table 1: $v_{\rm AO}$ and r₀ contributions to the coherence wavefront time $\tau_{\rm AO}$ over Paranal (40-th grid point in Fig. 11b) and the coast (11-teen grid point in Fig. 11b). In the first two lines are reported the values of $\tau_{\rm AO}$, $v_{\rm AO}$ and r₀ computed over the whole atmosphere [0-20] km. In the next lines are reported the same parameters computed on the near ground atmosphere [0-4] km and the free atmosphere [4-20] km

  

Figure 12: Horizontal maps of the parameters showed in Fig. 11 simulated on the same surface as selected by the dashed lines in Fig. 1. a) Seeing $\varepsilon$. Color code: values between [0 - 1.6] arcsec are represented with a step of 0.2 arcsec. Red regions are related to a bad seeing, blu regions to a good seeing. b) Coherence wavefront time $\tau_{\rm AO}$. Color code: values between [0 - 10] msec are represented with a step of 1 msec. Red regions are related to a great $\tau_{\rm AO}$, blue regions to a low $\tau_{\rm AO}$. c) Isoplanatic angle $\theta_{\rm AO}$. Color code: values between [1 - 4] arcsec are represented with a step of 0.25 arcsec. Red regions are related to a great $\theta_{\rm AO}$, blue regions to a low $\theta_{\rm AO}$. d) Scintillation rate $\sigma ^{2}_{\rm I}$. Color code: values between [0 - 50]% are represented with a step of 10%. Red regions are related to a strong scintillation, blue regions to a low scintillation. e) Spatial coherence outer scale ${\cal L}_0$. Color code: values between [1 - 10] m are represented with a step of 1 m. Red regions are related to a great ${\cal L}_0$, blue regions to a small ${\cal L}_0$. Colour figure on Web A&AS site

In Fig. 11b and Fig. 12b one can remark, over the coast, the minimum value for the coherence wavefront time $\tau_{\rm AO}$. What is the reason of such a different behavior of $\tau_{\rm AO}$ over the coast and over the Paranal? This parameter, defined in Eq. (27), depends on the 5/3 power of the wind intensity and on a linear power of the $C_{\rm N}^2$. Which of these two parameters has the greatest impact on the $\tau_{\rm AO}$? The turbulence above the coast is stronger than that above the Paranal (Fig. 10). The altitudes characterized by the strongest wind (jet-stream) are typically 12 km and, at this fixed altitude z, the wind intensity can reach 60 m/s but it is quite constant over the x, y direction. The wind intensity in the low atmosphere blows at a slower intensity [1-10] m/s but it is generally more variable in the x, y direction. In order to better discriminate the different contributions provided by the turbulence ($C_{\rm N}^2$ profiles) and the velocity $v_{\rm AO}$ in the $\tau_{\rm AO}$ estimation Eq. (27) we computed (Table 1) the r₀, $v_{\rm AO}$ and $\tau_{\rm AO}$ over the whole atmosphere [0-20] km, the first [0-4] km and the remaining [4-20] km above the Paranal mountain (40-th grid point in Fig. 11b) and the coast (11-th grid point). Analyzing the results obtained over the whole atmosphere one can observe that the ratio $r_{\rm 0,P}/r_{\rm 0,C}$ is $\sim 25$ and $v_{\rm AO,P}/v_{\rm AO,C}$ is $\sim 2$. One can deduce that, in this case, the extremely little value of r₀ is the principal cause of the strong decrease of $\tau_{\rm AO}$ above the coast. Moreover, we can affirm that such a little value of r₀ is ascribed to near ground turbulence. In fact, we find over [0-4] km the same r₀ = 1.33 cm computed over the whole atmosphere. $\tau_{\rm AO}$ becomes sensitive to the fluctuations of the velocity $v_{\rm AO}$ when we analyze only the free atmosphere turbulence [4-20] km contributions. In this part of the atmosphere the ratio $r_{\rm 0,C}/r_{\rm 0,P}$ is $\sim 1.14$ and $v_{\rm AO,P}/v_{\rm AO,C}$ is $\sim 1.49$, that is, in this case, the contributions provided by the $v_{\rm AO}$ variation is greater than the r₀ one and, ignoring the first 4 kilometers, $\tau_{\rm AO,C}\gt\tau_{\rm AO,P}$.

As the coherence wavefront time, the isoplanatic angle (Fig. 11c, Fig. 12c) decreases over the coast. It maintains a more or less constant value over the interior region. One can observe that, in this case, the principal cause of a decreasing value of $\theta_{\rm AO}$, from 0.3 to 0.1 arcsec, is the near ground turbulence present above the coast.

The scintillation profile is strongly correlated to the seeing one (Fig. 11a, Fig. 11c). A uniform value is observed on the broad central region except for two little peaks at about 10 km to the east and west of Paranal. In Fig. 12c) one can remark a non realistic value ($\sigma ^{2}_{\rm I}$ > 1) of the scintillation rate above the chilean coast. This is due to the fact that Eq. (24) is obtained with the weak perturbation theory (Tatarski 1995), which is not verified in this area. It is known that the scintillation rate is proportional to the $C_{\rm N}^2$ $\cdot$ $\delta h$ turbulence intensity only in the range $\sigma ^{2}_{\rm I}$ < 0.3. For a greater $C_{\rm N}^2$ $\delta h$ values the $\sigma ^{2}_{\rm I}$ reaches a saturated value of about 1. This means that any $\sigma ^{2}_{\rm I}$ value greater of this threshold is not significant. Finally, one can observe in Fig. 11e and Fig. 12e that the outer scale ${\cal L}_0$increases above the region of maximum $C_{\rm N}^2$ production, that is over the coast, and at about 10 km at the east of the Paranal. One notes that the spatial outer scale reaches very low values over the Paranal area (< 1 m). In spite of the still open discussion in the astronomic community about the ${\cal L}_0$estimation, these values agree with those found by some authors (Nightingale et al. 1991; Fuchs 1995) and they are supported by the physical mechanism recently proposed (Coulman et al. 1995) to explain the optical turbulence formation.

  

Figure 13: Temporal evolution of the $C_{\rm N}^2$ profiles simulated for the 3/11/95 night over the Roque de Los Muchachos Observatory in Canaries Isles. Colour figure on Web A&AS site

In the introduction of this paper we remembered that all the parameters affected by the optical turbulence have a stochastic behavior. During a night, thin turbulent layers can appear and disappear at different altitudes and times. Most simulation results presented here are sampled at an interval time of the order of 30 minutes or 1 hour. In order to fill this lack of information in the temporal scale we modified the code to have a further output. It is now possible to follow the temporal evolution of the $C_{\rm N}^2$ profiles simulated at a precise point (x₀,y₀) with a sampling time of about 2 minute. In Fig. 13 is reported an example of such a temporal $C_{\rm N}^2$(h, t) output obtained over Roque de los Muchachos site in Canaries Isles. One can remark the presence of a strong turbulent layer at ground level, persisting during the whole night and a more variable turbulent structure at about 10 km. It is interesting to note that, during the first 30 minutes, the model has not yet reached an orographic adaptation. This tool could make simpler a comparison with Scidar measurements and it could be helpful to better define the forecast time.