

Up: 3D mapping of optical
Subsections
The Meso-Nh Atmospheric Simulation System (Lafore et al. 1998) can simulate the time evolution of
the atmospheric three dimensional motions ranging from the large meso-alpha
scale (100 km) down to the typical microscale of the Large Eddy Simulation
(LES) models (50 m). It can forecast several meteorological variables on its 3D computation grid:
the three components of the wind, the temperature, the moisture, the
pressure and the turbulence kinetic energy. An optical
turbulence scheme has been added later and is sketched in Sect. 3.3
(seeing 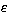 ,
, 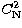 profiles, isoplanetic angle
profiles, isoplanetic angle 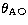 , scintillation rate
, scintillation rate 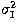 ,
coherence wavefront time
,
coherence wavefront time 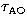 and spatial coherence outer scale
and spatial coherence outer scale 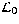 ).
Meso-Nh is a non-hydrostatic numerical
model (Lafore et al. 1998) based on the anelastic approximation. The principal characteristic of this
approximation is that all acoustic waves are filtered but nevertheless, the model can represent accurately the
gravity waves that enhance the shear production of turbulence. The lee waves occurring downstream of the mountain ranges and resulting
in flow deceleration are particularly well simulated by this model. These waves
can perturb the flow and increase the level of the turbulence activity. Using a high model resolution,
we need a non-hydrostatic model
to resolve the orographic effects in the turbulence developement
and obtain a more accurate estimation of the turbulent kinetic energy because
such a model describes this physical phenomenon.
).
Meso-Nh is a non-hydrostatic numerical
model (Lafore et al. 1998) based on the anelastic approximation. The principal characteristic of this
approximation is that all acoustic waves are filtered but nevertheless, the model can represent accurately the
gravity waves that enhance the shear production of turbulence. The lee waves occurring downstream of the mountain ranges and resulting
in flow deceleration are particularly well simulated by this model. These waves
can perturb the flow and increase the level of the turbulence activity. Using a high model resolution,
we need a non-hydrostatic model
to resolve the orographic effects in the turbulence developement
and obtain a more accurate estimation of the turbulent kinetic energy because
such a model describes this physical phenomenon.
The input data required by
the model are:
- a numerical terrain model with high spatial resolution;
- the fields of atmospheric pressure, temperature, humidity and wind
known at an initial time t0. One
can use either analyses provided by Meteorologic Centers or radiosoundings
provided by Meteorological Stations.
The basic equations of the model that are used to compute the time
evolution of the physical system are the conservation of momentum
(equations of motion), the first law of thermodynamics combined with equation of state and the equations of
dry-air-mass and moisture conservation. The turbulence is among the physical
processes that occur at scales too small to be resolved by the model and so it
must be parameterized. Although the model offers a choice of 3D turbulent schemes,
we used a 1D mode which takes into account only the vertical turbulent
fluxes.
The method used to describe the turbulence
production is detailed in previous papers (Bougeault et al. 1995, 1989). It
relies on the turbulence kinetic energy equation which takes the following
form in Meso-Nh (Cuxart et al. 1995):
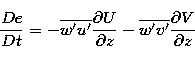
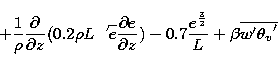
where the first and second term on the right hand side represent the shear production, the third
term the diffusion and the fourth term the dissipation. The
last term is the buoyancy term: 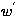 is the vertical wind
fluctuation,
is the vertical wind
fluctuation, 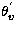 the virtual potential temperature
fluctuation and
the virtual potential temperature
fluctuation and 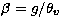 (g is the gravity
acceleration). The vertical fluxes of wind and temperature are parameterized
following the eddy diffusivity approach:
(g is the gravity
acceleration). The vertical fluxes of wind and temperature are parameterized
following the eddy diffusivity approach:
| 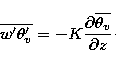 |
(3) |
The physical parameterizations are somewhat different from those of the
previous hydrostatic model Peridot (Bougeault 1995) developed at the CNRM
in Toulouse (Fr).
In the Peridot model, the eddy diffusivity is given by:
| 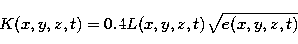 |
(4) |
where L is a mixing
length. In Meso-Nh the eddy diffusivity is a function given by:
| 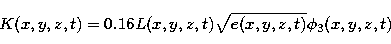 |
(5) |
where 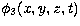 is an inverse turbulent Prandtl number.
is an inverse turbulent Prandtl number.
L2/e behaves in a different ways in stable and unstable layers.
In a very stable layer the mixing length is nearly equivalent to the
Deardoff length
| 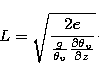 |
(10) |
Replacing Eq. (10) in Eq. (9) leads to 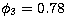 .
In a very unstable layer
.
In a very unstable layer 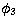 takes larger
values and an upper bound is set as
takes larger
values and an upper bound is set as 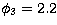 , based on theoretical and experimental results.
, based on theoretical and experimental results.
Finally, if we substitute Eqs. (5) in (3), we obtain the microscopic
quantities related to
the macroscopic variables L, e and 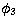 .
.
| 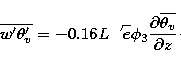 |
(11) |
The Meso-Nh model has been adapted to simulate the optical atmospheric
turbulence which is estimated by measuring the structure constant of the
temperature fluctuations (Wyngaard et al. 1971; André et al. 1978;
Coulman et al. 1986):
| 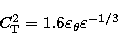 |
(12) |
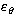 is the rate of temperature variance
destruction by viscous processes
and
is the rate of temperature variance
destruction by viscous processes
and 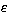 is the rate of energy dissipation related to the
turbulence characteristic length L and the energy e by the Kolmogorov law
is the rate of energy dissipation related to the
turbulence characteristic length L and the energy e by the Kolmogorov law
| 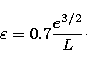 |
(13) |
Equation (12) assumes that 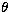 is a passive additive constituent. This is not true in general since
buoyancy forces are associated with temperature inhomogeneities and those buoyancy forces are taken into
account in other aspects of our computation by the
is a passive additive constituent. This is not true in general since
buoyancy forces are associated with temperature inhomogeneities and those buoyancy forces are taken into
account in other aspects of our computation by the  term. This theory is based on the analogy between the velocity
fluctuations in a turbulent flow and the concentration fluctuations of a
conservative passive additive
term. This theory is based on the analogy between the velocity
fluctuations in a turbulent flow and the concentration fluctuations of a
conservative passive additive 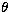 in a turbulent flow. It is based on a
law that links the microscopic and the macroscopic physical parameters.
The prognostic equation of the potential temperature variance
in a turbulent flow. It is based on a
law that links the microscopic and the macroscopic physical parameters.
The prognostic equation of the potential temperature variance 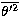 in the turbulent energy budget is (André et al. 1978):
in the turbulent energy budget is (André et al. 1978):
| 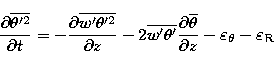 |
(14) |
where 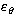 is the molecular dissipation and
is the molecular dissipation and 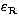 the radiative
dissipation. Assuming that we can neglect
the contributions from the triple correlations
the radiative
dissipation. Assuming that we can neglect
the contributions from the triple correlations 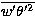 and the radiative dissipation we have
and the radiative dissipation we have
| 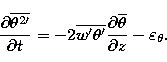 |
(15) |
The steady state balance equation for the rate of destruction of the variance leads to:
| 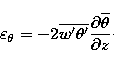 |
(16) |
If we substitute (16) and (13) into (12) using
Eq. (11) presented in the last paragraph we obtain 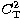 expressed as a function of macroscopic variables only
expressed as a function of macroscopic variables only
| 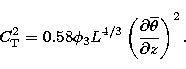 |
(17) |
Finally, the structure constant of the refraction index is obtained using the
Gladstone's law:
| 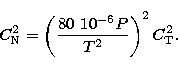 |
(18) |
Today we need to measure seeing and
other parameters such as the coherence wavefront time (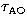 ), the
isoplanatic angle (
), the
isoplanatic angle (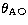 ) and the spatial coherence outer scale
(
) and the spatial coherence outer scale
(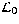 ). All these parameters
are related to the refractive index fluctuations which appear inside the
atmospheric turbulent layers and to the wind velocity profile. We summarize, in the following, the parameters
which have been coded in the model. All the following parameters are referred to the zenith
direction. Starting from the Fried parameter r0
given by:
). All these parameters
are related to the refractive index fluctuations which appear inside the
atmospheric turbulent layers and to the wind velocity profile. We summarize, in the following, the parameters
which have been coded in the model. All the following parameters are referred to the zenith
direction. Starting from the Fried parameter r0
given by:
| ![\begin{displaymath}
r_{0}=\left[ 0.423\left( \frac{2\pi }{\lambda }\right)
^{2}...
...}^{\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h\right] ^{-3/5}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img54.gif) |
(19) |
the seeing 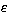 , defined as the width at the half
height of a star image at the focus of a large diameter telescope
was expressed as follows (Roddier 1981):
, defined as the width at the half
height of a star image at the focus of a large diameter telescope
was expressed as follows (Roddier 1981):
| 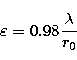 |
(20) |
where  is the optical wavelength. As others authors we choose
is the optical wavelength. As others authors we choose
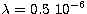 m for this study.
m for this study.
The isoplanatic angle 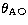 (Roddier et al. 1982; Fried 1979) defined as the
maximum angular separation of two stellar objects producing similar
wavefronts at the telescope entrance pupil, has the following analytical
expression:
(Roddier et al. 1982; Fried 1979) defined as the
maximum angular separation of two stellar objects producing similar
wavefronts at the telescope entrance pupil, has the following analytical
expression:
| 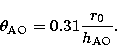 |
(21) |
Knowing that the seeing layer 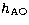 is a sort of average distance weighted by a 5/3 power law
is a sort of average distance weighted by a 5/3 power law
| ![\begin{displaymath}
h_{\rm AO}=\left[ \frac{\int\limits_{0}^{\infty }h^{5/3}C_{\...
...}^{\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h}\right] ^{3/5}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img60.gif) |
(22) |
we obtain
| 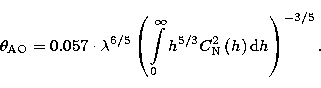 |
(23) |
The scintillation rate (Roddier 1981) was expressed as follows
| 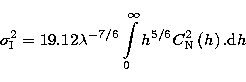 |
(24) |
The coherence wavefront time 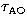 (Roddier et al. 1982) is:
(Roddier et al. 1982) is:
| 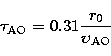 |
(25) |
where
| ![\begin{displaymath}
\upsilon _{\rm AO}=\left[
\frac{\int\limits_{0}^{\infty}\le...
...{\infty }C_{\rm N}^{2}
\left( h\right) {\rm d}h }\right] ^{3/5}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img64.gif) |
(26) |
and 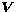 (h) is the horizontal wind velocity vector. Thus,
(h) is the horizontal wind velocity vector. Thus, 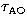 can be expressed as:
can be expressed as:
| ![\begin{displaymath}
\tau _{\rm AO} = 0.057 \cdot\lambda^{6/5}
\left[\int\limits_...
...ert
^{5/3}C_{\rm N}^{2}\left(h\right) {\rm d}h\right]^{-3/5} .\end{displaymath}](/articles/aas/full/1999/10/ds7850/img65.gif) |
(27) |
Finally, the spatial coherence outer scale
(Borgnino 1990)
| ![\begin{displaymath}
{\cal L}_{0}=\left[\frac{\int\limits_{0}^{\infty }
{L(h)}^{-...
...0}^{\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h}
\right]^{-3}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img66.gif) |
(28) |
where L is the Bougeault-Lacarrere mixing length defined in Sect. 3.2.


Up: 3D mapping of optical
Copyright The European Southern Observatory (ESO)
![]() ,
, ![]() profiles, isoplanetic angle
profiles, isoplanetic angle ![]() , scintillation rate
, scintillation rate ![]() ,
coherence wavefront time
,
coherence wavefront time ![]() and spatial coherence outer scale
and spatial coherence outer scale ![]() ).
Meso-Nh is a non-hydrostatic numerical
model (Lafore et al. 1998) based on the anelastic approximation. The principal characteristic of this
approximation is that all acoustic waves are filtered but nevertheless, the model can represent accurately the
gravity waves that enhance the shear production of turbulence. The lee waves occurring downstream of the mountain ranges and resulting
in flow deceleration are particularly well simulated by this model. These waves
can perturb the flow and increase the level of the turbulence activity. Using a high model resolution,
we need a non-hydrostatic model
to resolve the orographic effects in the turbulence developement
and obtain a more accurate estimation of the turbulent kinetic energy because
such a model describes this physical phenomenon.
).
Meso-Nh is a non-hydrostatic numerical
model (Lafore et al. 1998) based on the anelastic approximation. The principal characteristic of this
approximation is that all acoustic waves are filtered but nevertheless, the model can represent accurately the
gravity waves that enhance the shear production of turbulence. The lee waves occurring downstream of the mountain ranges and resulting
in flow deceleration are particularly well simulated by this model. These waves
can perturb the flow and increase the level of the turbulence activity. Using a high model resolution,
we need a non-hydrostatic model
to resolve the orographic effects in the turbulence developement
and obtain a more accurate estimation of the turbulent kinetic energy because
such a model describes this physical phenomenon.
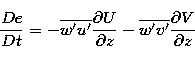
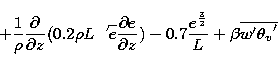
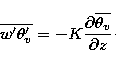

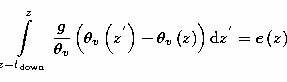
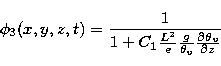
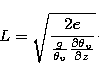
![]() .
.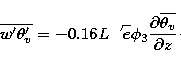
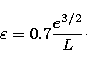
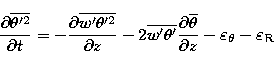
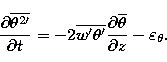
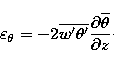
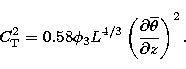
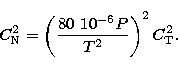
![]() ), the
isoplanatic angle (
), the
isoplanatic angle (![]() ) and the spatial coherence outer scale
(
) and the spatial coherence outer scale
(![]() ). All these parameters
are related to the refractive index fluctuations which appear inside the
atmospheric turbulent layers and to the wind velocity profile. We summarize, in the following, the parameters
which have been coded in the model. All the following parameters are referred to the zenith
direction. Starting from the Fried parameter r0
given by:
). All these parameters
are related to the refractive index fluctuations which appear inside the
atmospheric turbulent layers and to the wind velocity profile. We summarize, in the following, the parameters
which have been coded in the model. All the following parameters are referred to the zenith
direction. Starting from the Fried parameter r0
given by:
![\begin{displaymath}
r_{0}=\left[ 0.423\left( \frac{2\pi }{\lambda }\right)
^{2}...
...}^{\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h\right] ^{-3/5}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img54.gif)
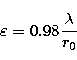
![]() (Roddier et al. 1982; Fried 1979) defined as the
maximum angular separation of two stellar objects producing similar
wavefronts at the telescope entrance pupil, has the following analytical
expression:
(Roddier et al. 1982; Fried 1979) defined as the
maximum angular separation of two stellar objects producing similar
wavefronts at the telescope entrance pupil, has the following analytical
expression:
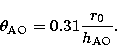
![\begin{displaymath}
h_{\rm AO}=\left[ \frac{\int\limits_{0}^{\infty }h^{5/3}C_{\...
...}^{\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h}\right] ^{3/5}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img60.gif)
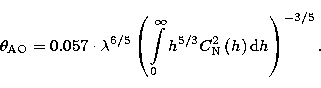
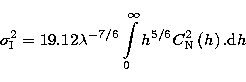
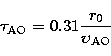
![\begin{displaymath}
\upsilon _{\rm AO}=\left[
\frac{\int\limits_{0}^{\infty}\le...
...{\infty }C_{\rm N}^{2}
\left( h\right) {\rm d}h }\right] ^{3/5}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img64.gif)
![\begin{displaymath}
\tau _{\rm AO} = 0.057 \cdot\lambda^{6/5}
\left[\int\limits_...
...ert
^{5/3}C_{\rm N}^{2}\left(h\right) {\rm d}h\right]^{-3/5} .\end{displaymath}](/articles/aas/full/1999/10/ds7850/img65.gif)
![\begin{displaymath}
{\cal L}_{0}=\left[\frac{\int\limits_{0}^{\infty }
{L(h)}^{-...
...0}^{\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h}
\right]^{-3}\end{displaymath}](/articles/aas/full/1999/10/ds7850/img66.gif)