5 Derivation of proper motions

  The proper motion of a Tycho star was derived from its position at epoch J1991.25, as given in the Tycho Catalogue, and the AC observations identified with it. Although the typical number of AC observations per Tycho star is two, 20183 Tycho stars with only one observation in AC were also accepted for TRC.

5.1 Least-squares adjustment

  The derivation of proper motions followed the standard weighted least-squares fit procedure, applied if more than two positions per star were available. The constraint on the upper limit of the Tycho proper motion modulus (cf. Sect. 4.2) allowed to use the simple linear model:

 

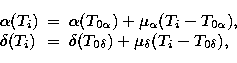
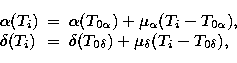$$\begin{array} {lcl} \alpha(T_i) & = & \alpha(T_{0\alpha}) ... ...a(T_{0\delta}) + \mu_{\delta} (T_i-T_{0\delta}),\\ \end{array}$$ (6)

where the meaning of the various symbols is as follows: $T_{0\alpha}$,$T_{0\delta}$ - the weighted mean epochs of right ascension and declination; $\alpha(T_{0\alpha})$, $\delta(T_{0\delta})$ - the weighted means of right ascension and declination at epoch $T_{0\alpha}$ and $T_{0\delta}$; T_i, $\alpha(T_i)$, $\delta(T_i)$ - epoch, right ascension, and declination of the individual observation; $\mu_{\alpha}$ and $\mu_{\delta}$ - resulting proper motion components in right ascension and declination.

The individual positions were weighted by the inverse square of their respective standard errors. Those of the Tycho positions were defined by the published standard errors of right ascension and declination, while those of the AC positions were estimated from the rms scatter of the plate reduction residuals (the same for all measurements on a given plate) and estimates for the systematic errors of the individual positions, based on the covariance matrix of the plate parameters derived at step 3 of the reduction procedure (see Sect. 3). The Tycho Catalogue data is treated as one observation per star in this context.

The chi-square of the residuals after each least-squares adjustment was compared with the expected value. Any large discrepancy indicates a problem case due to misidentification, unresolved duplicity etc. Stars with one of the chi-squares (for $\alpha$ or $\delta$) exceeding a certain limit were rejected. The rate of such rejections was 1.31%.

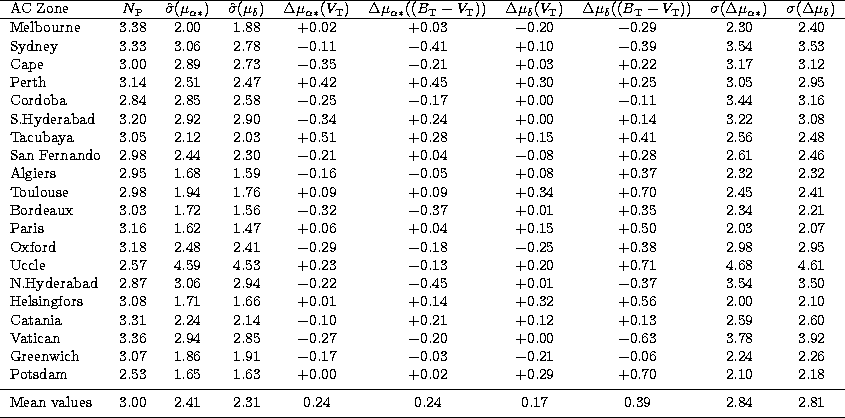
The rms internal estimates of the errors of the preliminary proper motion components, $\hat{\sigma}(\mu_{\alpha*})$ and $\hat{\sigma}(\mu_{\delta})$, derived from the covariance matrices of Eqs. (6), are given in Table 3. The estimates are provided separately for each zone to emphasize the effects of the zonal structure of the Astrographic Catalogue, e.g. the impact of the smaller epoch difference to the Tycho data in the AC zones covering the original Potsdam zone. The rms all-sky $\hat{\sigma}(\mu_{\alpha*})$ and $\hat{\sigma}(\mu_{\delta})$ values for the 990 182 TRC stars are 2.37 and 2.27 mas/yr respectively. These are slightly different from the corresponding values listed in the last row of Table 3 due to the zonal overlaps, i.e. the one-degree declination strips on the border of any two AC zones, covered by both of them.

  

Table 3: Estimated random and systematic accuracy of the preliminary TRC proper motions, for each AC zone. The individual columns denote: mean number of positions used to derive proper motions ($N_{\rm P}$), rms internal standard error of the preliminary proper motions in units of mas/yr ($\hat{\sigma}(\mu_{\alpha*})$ and $\hat{\sigma}(\mu_{\delta})$), residual magnitude and colour equation as estimated from the differences TRC(prelim)-Hipparcos (in units of mas/yr/mag), and standard deviations of the preliminary TRC proper motions from Hipparcos ($\sigma(\Delta\mu_{\alpha*})$ and $\sigma(\Delta\mu_{\delta})$)

5.2 Investigation of the systematic errors of the preliminary proper motions

In order to investigate the reliability of the internal error estimates, the preliminary TRC proper motions were compared with those from the Hipparcos Catalogue. The comparison was based on 93078 stars common to the two catalogues. The distribution of the differences is shown in Fig. 8; the standard deviations are 2.73 mas/yr in $\mu_{\alpha*}$ and 2.69 mas/yr in $\mu_{\delta}$.Comparing the latter with the rms value of the internal error estimates (2.37/2.27 mas/yr) and taking into account rms standard error of the Hipparcos proper motions (1.25 mas/yr per component), we conclude that the preliminary TRC proper motions include residual systematic errors of the order of 1 mas/yr.

  

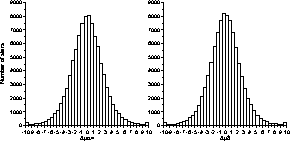Figure 8: Differences of the preliminary TRC and Hipparcos proper motions, in units of mas/yr, based on 93078 common stars

Probable sources of the residual systematic errors are suggested by the nature of the internal error estimates. These represent only the random errors of the individual positions and a part of the residual plate-scale systematic errors. Errors not covered by the internal estimates include:

• errors of the reference system realization at the AC epoch (caused by the residual systematic errors of the improved ACRS used as an intermediate reference catalogue for the AC reduction), and
• residual magnitude and colour equations in the AC data.

Zonal analysis of the preliminary TRC-Hipparcos differences confirmed that the systematic errors are mainly caused by the residual magnitude equation in the AC data. Estimates of the residual magnitude and colour equations in the preliminary TRC proper motions, derived by linear interpolation from the comparison with Hipparcos, are listed in Table 3; on the average, the errors amount to 0.25 mas/yr/mag each.

It should be noted that the residual magnitude and colour equations found in the preliminary TRC proper motions are not independent. This is explained by the strong correlation between colour and magnitude of the Tycho Catalogue stars: for example, if stars common to TRC and Hipparcos are divided according to the median $(B_{\mathrm{T}}-V_{\mathrm{T}})$ colour index (0.64 mag) into a "blue" and a "red" subset, the median magnitude is $B_{\mathrm{T}}= 8.8$ mag for the "blue''$\!\!$, and $B_{\mathrm{T}}= 9.8$ mag for the "red" one. Additional investigation had shown magnitude equation to be the dominant effect, and the colour equation was therefore ignored in the derivation of further systematic corrections.

5.3 Correction of the zonal magnitude equation

  As mentioned above (cf. Sect. 3.7), the plate adjustment approach used to reduce the AC onto the Hipparcos system cannot completely remove the magnitude equation, primarily due to the insufficient density of the reference catalogue. For the same reason we cannot derive completely adequate a-posteriori correction of the residual magnitude equation found in the preliminary TRC proper motions. To account at least for the major part of the effect, declination-dependent linear corrections were derived from comparison with Hipparcos.

In order to derive the corrections, the differences between the preliminary TRC and the Hipparcos proper motions for common stars were organized into a table of $(\delta, \Delta\mu_{\alpha*}, \Delta\mu_{\delta})$ and sorted according to increasing declination. Batches of 500 successive rows of this table with 50 per cent overlap were then used. In each batch, the stars were divided according to $B_{\mathrm{T}}$ in two equal subsets, and the median values of the magnitude and of the differences in proper motion components were calculated for each subset. The magnitude equation was then assumed to be linear through the two points, but was truncated for magnitudes brighter than $B_{\mathrm{T}}=6.5$ mag to avoid large, unwarranted corrections for very bright stars. For each batch the linear magnitude equation estimate was calculated in the form of the intercept at $B_{\mathrm{T}}=9.35$ mag (in mas/yr) and the slope (in mas/yr/mag). These corrections were then applied to the preliminary TRC to yield the final proper motions.