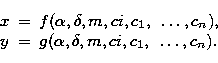
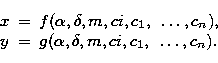 |
(1) |
The meaning of individual symbols in Eqs. (1) is as
follows: x and y - image coordinates of the star as measured on the
plate; ![]() - equatorial coordinates of the star referred to
some chosen reference system; m, ci - its magnitude and colour; f and
g - gnomonic projections supplemented by additional (usually polynomial)
terms describing various plate-scale effects like tilt, coma etc.;
- equatorial coordinates of the star referred to
some chosen reference system; m, ci - its magnitude and colour; f and
g - gnomonic projections supplemented by additional (usually polynomial)
terms describing various plate-scale effects like tilt, coma etc.;
![]() - the unknown parameters of the latter (so-called
plate constants).
- the unknown parameters of the latter (so-called
plate constants).
The plate reduction proper is the derivation of the unknowns ![]() through Eqs. (1). Obtained plate constants then allow to
solve Eqs. (1) for the equatorial coordinates
through Eqs. (1). Obtained plate constants then allow to
solve Eqs. (1) for the equatorial coordinates ![]() and
and ![]() of all stars measured on a plate or a set of plates.
of all stars measured on a plate or a set of plates.
Under the common approach to reduction, the so-called conventional plate
adjustment, unknowns ![]() are derived based on stars with
known position at epoch of the plate exposure (i.e. reference stars).
For the reduction to proceed, it is first necessary to investigate the
significant plate-scale systematic errors or, in other words, to establish
the functional form of f and g in Eqs. (1). Since
neither normal astrographs nor measuring devices used throughout the AC
project are anymore available for laboratory testing and calibration in their
original state, the only method to investigate telescope-specific aberrations
and measuring machine errors is to analyze the residuals after conventional
plate adjustment. When the form of f and g - that is, the plate
model - is established, a reduction of the AC data can proceed.
are derived based on stars with
known position at epoch of the plate exposure (i.e. reference stars).
For the reduction to proceed, it is first necessary to investigate the
significant plate-scale systematic errors or, in other words, to establish
the functional form of f and g in Eqs. (1). Since
neither normal astrographs nor measuring devices used throughout the AC
project are anymore available for laboratory testing and calibration in their
original state, the only method to investigate telescope-specific aberrations
and measuring machine errors is to analyze the residuals after conventional
plate adjustment. When the form of f and g - that is, the plate
model - is established, a reduction of the AC data can proceed.
The establishment of the AC zone-specific plate models followed this
approach. It started with a so-called Turner plate model, in which
f and g are linear functions of the standard coordinates (rectangular
coordinates on the plate derived from ![]() ,
, ![]() through gnomonic
projection with an assumed plate centre). After the least-squares solution of
Eqs. (1) residuals from all plates of a zone were
combined and analyzed for higher-order terms which significantly improve the
model with respect to the chosen statistical criteria. The additional plate
model terms defined in this way - the zone-specific corrections -
may represent known physical phenomena (which is welcome), or be purely ad
hoc (which cannot be entirely avoided).
through gnomonic
projection with an assumed plate centre). After the least-squares solution of
Eqs. (1) residuals from all plates of a zone were
combined and analyzed for higher-order terms which significantly improve the
model with respect to the chosen statistical criteria. The additional plate
model terms defined in this way - the zone-specific corrections -
may represent known physical phenomena (which is welcome), or be purely ad
hoc (which cannot be entirely avoided).
To investigate significant plate-scale systematics in such a way, the number
of reference stars per plate should be sufficient for a reliable determination
of the parameters ![]() . However, the representation of the ICRS
system by the
Hipparcos Catalogue is too sparse for this purpose, providing an average 3
stars per square degree. Inapplicability of the Hipparcos for this purpose
necessitated the employment of a denser intermediate reference catalogue and
the development of a specific three-step plate adjustment procedure.
. However, the representation of the ICRS
system by the
Hipparcos Catalogue is too sparse for this purpose, providing an average 3
stars per square degree. Inapplicability of the Hipparcos for this purpose
necessitated the employment of a denser intermediate reference catalogue and
the development of a specific three-step plate adjustment procedure.
First, the plates constituting an AC zone were reduced on the "Astrographic Catalogue Reference Stars'' (ACRS, Corbin & Urban 1991) catalogue system by adjusting the 6 parameters of the Turner plate model. The residuals were then analyzed to yield additional terms. These then formed the advanced reduction model that accounts for the significant plate-scale systematic errors specific to the AC zone in question.
In step 2 the solution was repeated, but this time with the significant plate-scale terms found in step 1 added to the plate model. The ACRS again served as reference catalogue. The derived plate parameters were then analyzed for any dependence on observation/measurement conditions and other factors. Based on the results of this analysis, plates of the zone were, if necessary, discriminated into subsets. Subsequent averaging of the higher-order plate parameters yielded the final zone-specific (or subset-specific) systematic corrections.
In the third step the final reduction onto the Hipparcos system was performed using the Turner model and the Hipparcos Catalogue as reference catalogue. The zone-specific systematic corrections derived in step 2 were applied beforehand. If, for example, step 1 suggested that a sizeable cubic distortion is present for a specific astrograph, the distortion coefficient was estimated for all plates in step 2. The estimates from individual plates were then averaged to yield a unique value, assumed to be characteristic for the astrograph. At step 3, that cubic distortion correction was then applied to all stars, as function of the actually measured plate coordinates.
The three-step approach using zone-specific corrections may be considered as an abridged plate overlap solution (Eichhorn 1960) in the sense that it assumes the instrument-specific parameters (e.g. the distortion coefficient) the same for all plates of the set, thus utilizing an important piece of information being lost under the individual plates adjustment approach. On the other hand, zone-specific plate models established under the present study provide the necessary basis for the future global block adjustment of the AC data.
At present, only two reference catalogues of the required density are available: "Astrographic Catalogue Reference Stars'' (ACRS, Corbin & Urban 1991), and "Positions and Proper Motions'' (PPM, Röser & Bastian 1991; Bastian et al. 1993), both utilizing practically all meridian and photographic observations of stars brighter than about B=9.5 mag available by 1990. PPM is distinguished as the first major application of the Astrographic Catalogue for the derivation of proper motions. It should be noted that the AC reduction performed for PPM was limited to stars brighter than about B=9.5 mag. Though it amounts only to about 10% of the Astrographic Catalogue stars, PPM is nonetheless correlated with AC and, consequently, cannot be applied for the investigation of systematic errors in AC. This leaves only ACRS as a suitable intermediate reference catalogue.
Prior to the application of ACRS to the investigation of systematic errors present in the AC data, it is necessary to remove the systematic errors of ACRS itself. Such errors were found in a comparison with Hipparcos during the TRC pilot project study (Kuzmin et al. 1997b). The errors amount to 250 mas in position at mean epoch and 5 mas/yr in proper motion (cf. Fig. 2). If unaccounted for, they would result in systematic errors of up to 500 mas when propagated to a typical AC epoch (the mean epoch difference between ACRS and AC is about 50 years).
Systematic differences of positions or proper motions given in any two catalogues may depend on position, magnitude and colour of the stars. The dependence on the latter two parameters, known as magnitude and colour equation respectively, has previously been difficult to investigate due to the absence of homogeneous set of magnitudes and colours for the large number of stars. Fortunately, the Tycho Catalogue photometry now provides the necessary basis for such an analysis.
Using the notation ![]() , we define
systematic differences between ACRS and Hipparcos as
, we define
systematic differences between ACRS and Hipparcos as
 |
(2) |
where the angle brackets denote averages over suitable sets of stars (e.g. cells of 25 square degrees, as in Fig. 2).
The analysis of the ACRS-Hipparcos differences had shown that the main contribution has the form of a declination-dependent magnitude equation and, to lesser extent, a colour equation, to the first order given by:
| |
(3) |
Here ![]() denotes one of the systematic differences defined in
Eqs. (2),
denotes one of the systematic differences defined in
Eqs. (2), ![]() and
and ![]() are Tycho blue magnitude and
colour, 9.15 mag is the mean of
are Tycho blue magnitude and
colour, 9.15 mag is the mean of ![]() and 0.768 mag the mean of
and 0.768 mag the mean of ![]() of
the stars common to ACRS and Hipparcos.
of
the stars common to ACRS and Hipparcos.
Figure 2 clearly identifies the zonal structure of the systematic differences between ACRS and Hipparcos positions and proper motions. Consequently, the coefficients b0, b1, and b2 in (3) should depend on spherical coordinates, mainly on declination. To account rigorously for the latter, a fairly complex analytical or numerical model would be necessary. Moreover, the number of stars common to ACRS and Hipparcos is insufficient for the statistically reliable determination of the coefficients of an analytical expansion of the differences (e.g. by spherical harmonics). A reasonable approach to correct ACRS systematic errors would thus be to re-reduce the positional catalogues underlying ACRS. Since this time-consuming effort did not fit into the time schedule of the TRC project, a simple numerical method was used:
To solve the problem in a consistent way, a pattern-matching algorithm was developed (Kuimov 1992). It does not require a transformation between the rectangular coordinate systems of the source (reference stars) and target (measurements) to be known. The algorithm analyzes the triangles formed by stars of the source and target lists in search for pairs of similar triangles (similarity is tested by matching the respective angles, so the approach does not even require source and target coordinate system scales to be the same). The pattern-matching algorithm was successful on all the 22652 Astrographic Catalogue plates, including all sorts of special cases.
The residual scatter of a conventional plate adjustment represents four main factors: the variance of the adopted plate parameters, systematic plate-scale effects unmodelled by the adopted plate model, random measurement errors, and the random errors of the reference star positions at the epoch of observation. Due to the early epoch of the Astrographic Catalogue, the reference catalogue's positional accuracy at the epoch of the plates is comparable to the measurement errors (e.g., about 200 mas for Hipparcos stars). Consequently, these two components dominate the rms scatter, which under such circumstances becomes a fairly insensitive estimate of the reduction quality. Another disadvantage of the residual scatter as a reduction quality estimate is that it is limited to the magnitude interval of the reference stars. Thus its application as an estimate for other, usually fainter, stars is a mere extrapolation.
Fortunately, the two-fold overlap of the Astrographic Catalogue plates provides a natural
estimator of the reduction quality - the variance of positions of the
same star derived from overlapping plates. To avoid a bias
introduced by proper motions, the estimate must be based only on plates with
insignificant epoch difference (less than, say, 5 years). Consider a subset
of AC plates containing ![]() stars with at least two measurements.
Let
stars with at least two measurements.
Let ![]() denote the total number of measurements, Si the
dispersion of the individual positions of star i,
denote the total number of measurements, Si the
dispersion of the individual positions of star i, ![]() , and S the sum of these dispersions over all stars. Then the
mean error of an individual position s and its standard deviation
, and S the sum of these dispersions over all stars. Then the
mean error of an individual position s and its standard deviation
![]() can be estimated as follows
(Hudson 1964)
can be estimated as follows
(Hudson 1964)
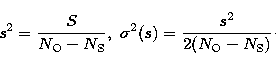 |
(4) |
The quantities ![]() and
and ![]() , given by Eqs. (4) for the
variance in right ascension and declination respectively, were used as a
reduction quality estimates. The error of an individual star position
includes a random part (measurement error) and a systematic part (reduction
error). Since the former is not expected to vary significantly if
measurements of the same star on overlapping plates are considered, smaller
, given by Eqs. (4) for the
variance in right ascension and declination respectively, were used as a
reduction quality estimates. The error of an individual star position
includes a random part (measurement error) and a systematic part (reduction
error). Since the former is not expected to vary significantly if
measurements of the same star on overlapping plates are considered, smaller
![]() and
and ![]() values should correspond to smaller systematic errors.
Moreover, due to the complete overlap, the estimates are based on all
AC stars observed at least twice, and thus they solve the accuracy estimation
problem for faint stars. Finally, the estimates are calculated from
measurements of the same star, not from the residuals between measurements
and reference star positions, and thus are not directly influenced by the
errors of the reference catalogue.
values should correspond to smaller systematic errors.
Moreover, due to the complete overlap, the estimates are based on all
AC stars observed at least twice, and thus they solve the accuracy estimation
problem for faint stars. Finally, the estimates are calculated from
measurements of the same star, not from the residuals between measurements
and reference star positions, and thus are not directly influenced by the
errors of the reference catalogue.
These reasons make the variance of positions from overlapping plates suitable for the assessment of the reduction quality, both for the establishment of the optimal reduction model and for the estimation of the accuracy of an individual star positions after the final reduction step (cf. Sect. 3.7).
Analysis of the residuals after the first step of the reduction procedure
suggested the following plate model to be optimal with respect to the minimum
systematic errors criterion:
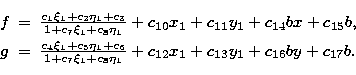 |
(5) |
The standard coordinates ![]() and
and ![]() in Eqs. (5)
were computed from the apparent positions of the reference stars. This
approach ensures that differential refraction and annual aberration are taken
into account prior to plate reduction, so that the plate parameters
in Eqs. (5)
were computed from the apparent positions of the reference stars. This
approach ensures that differential refraction and annual aberration are taken
into account prior to plate reduction, so that the plate parameters
![]() of Eqs. (5) characterize exclusively the
astrograph and measuring device errors.
of Eqs. (5) characterize exclusively the
astrograph and measuring device errors.
To illustrate the reduction approach outlined above, the next few sections cover the reduction of three AC zones: Melbourne, Hyderabad, and Algiers. Of these, the Melbourne zone is described in most detail; for the other two the emphasis is put on the zone-specific features.
The instrument used for taking the plates was a normal astrograph made by
"Grubb''. A total of 392584 images were measured with the aid of six
different measuring devices, some of micrometer screw and some of eyepiece
scale type. The measured coordinates are given to 1 ![]() m (0
m (0![]() 06); the
distribution of the digits in the last decimal place is close to uniform. The
brightness estimates are given in the form of measured image diameters for
bright stars and eye estimates for faint ones.
06); the
distribution of the digits in the last decimal place is close to uniform. The
brightness estimates are given in the form of measured image diameters for
bright stars and eye estimates for faint ones.
The residuals after the first step of the reduction procedure (using ACRS as the reference catalogue and a linear plate model) are shown in Figs. 4a and b. Two type of plots illustrate the plate-scale systematic errors and the errors of the secondary coordinate system, respectively.
Figure 5 shows the residuals in right ascension and declination
as functions of measured image diameter, with the magnitude equation in right
ascension clearly indicated. It is nonlinear and reaches 0![]() 3 for faint
stars. A magnitude equation of this type cannot be attributed to ordinary
aberrations of the optical system, nor to the atmospheric dispersion (plates
were taken close to the meridian, so the latter may cause a magnitude
equation in declination only). The most probable cause is a defect of the
objective lens, e.g. a decentering, or imperfect guiding.
3 for faint
stars. A magnitude equation of this type cannot be attributed to ordinary
aberrations of the optical system, nor to the atmospheric dispersion (plates
were taken close to the meridian, so the latter may cause a magnitude
equation in declination only). The most probable cause is a defect of the
objective lens, e.g. a decentering, or imperfect guiding.
In the third step, the final reduction on the Hipparcos system was performed using the Turner model and the Hipparcos Catalogue as reference. Corrections for the zone-specific systematic errors derived in step 2 were applied beforehand. The residuals after the final reduction are shown in Figs. 4-5.
 |
Figure 6: The plate parameter c15, characterizing the magnitude equation in right ascension, given for the AC Algiers plates as function of the year of observation |
The Algiers Observatory treated the zone ![]() to
to ![]() of declination.
Description of the observation and measurement procedures can be found in the
introduction to the published data
(Trepied 1903).
A total of 1260
plates were taken between 1891 and 1912, the mean plate epoch being J1904.2.
of declination.
Description of the observation and measurement procedures can be found in the
introduction to the published data
(Trepied 1903).
A total of 1260
plates were taken between 1891 and 1912, the mean plate epoch being J1904.2.
The plates were taken with the normal astrograph manufactured by "Henry
Brothers''. Coordinates of the 330449 images were measured with the aid of
micrometer screw devices, the usual practice for the French AC zones. The
measured coordinates are given to 0.1 ![]() m (0
m (0![]() 006). Magnitudes
derived from the measured image diameters are given for all stars.
006). Magnitudes
derived from the measured image diameters are given for all stars.
The Algiers observations were found to be among the best with respect to both random and systematic errors. Both plate-scale and measuring machine systematic errors are small and could be corrected very well. The overall magnitude equation in right ascension is close to zero, except for plates taken between 1900 and 1905 (Fig. 6). However, a subdivision of the plates into two sets according to the exposure date did not improve the overall reduction quality as estimated by the position variance criterion. Therefore it was rejected. It should be noted that the same feature was detected in the AC Bordeaux and Oxford data. In the latter case, the change in the magnitude equation may be associated with the adoption of a new emulsion. Unfortunately, the French observatories did not document the emulsion type being used.
The Nizamiah Observatory, located at Hyderabad, India, actually observed two
zones: ![]() to
to ![]() (referred to as
Hyderabad South), and
(referred to as
Hyderabad South), and
![]() to
to ![]() (Hyderabad North). The reduction of the southern
zone is described in the following, though the results apply to the northern
one as well.
(Hyderabad North). The reduction of the southern
zone is described in the following, though the results apply to the northern
one as well.
A description of the observation and measurement procedures can be found in the introduction to the published data (Pocock 1918). A total of 1260 plates for the Hyderabad South zone were taken between 1914 and 1929, the mean plate epoch being J1919.0. The coordinates of 521867 images were measured with an eyepiece scale device.
The Nizamiah Observatory was the only one of the participating institutions to use a non-standard objective, probably the so-called "Cook Triplet'', with the focal length of 3.37 m. The cubic distortion coefficient c9 of the Hyderabad telescope was found to depend on the air temperature at exposure time (cf. Fig. 7). The dependence was approximated by a one-year sinusoid, as shown in Fig. 7, to account for the effect. No such feature has been found in any other AC zone.
 |
The plate model given by Eqs. (5) and, for some AC
zones, the shortcut without magnitude-dependent terms, yielded the minimum
values of the reduction quality estimates ![]() and
and ![]() among all
reasonable models tried. Consequently, the AC reduction onto the Hipparcos
system relied on this plate model, considered as optimal with respect to the
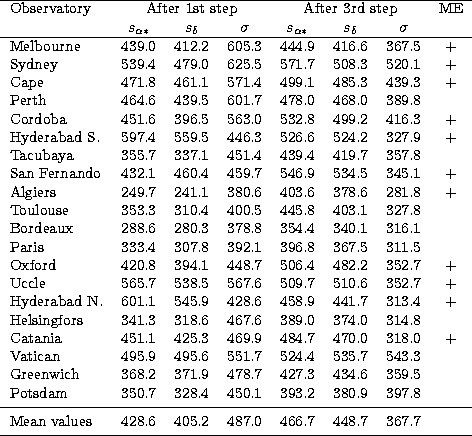
reduction quality estimates. Table 2 lists, for all zones of
the
Astrographic Catalogue, the reduction quality estimates along with rms scatter of the
residuals (in units of mas), both after the first step of the reduction
procedure (reduction onto the ACRS system by a linear model without
systematic corrections) and after the final reduction onto the Hipparcos
system, with zone-specific systematic corrections applied to the AC data.
among all
reasonable models tried. Consequently, the AC reduction onto the Hipparcos
system relied on this plate model, considered as optimal with respect to the
reduction quality estimates. Table 2 lists, for all zones of
the
Astrographic Catalogue, the reduction quality estimates along with rms scatter of the
residuals (in units of mas), both after the first step of the reduction
procedure (reduction onto the ACRS system by a linear model without
systematic corrections) and after the final reduction onto the Hipparcos
system, with zone-specific systematic corrections applied to the AC data.
The differentiation between plate models with and without magnitude-dependent terms is due to the fact that the magnitude equation is by far the most complicated type of systematic error found in the AC data. A noteworthy example of the non-linearity and complexity of the magnitude equation is the one detected in the Melbourne zone (cf. Fig. 5). Also a colour equation, though less pronounced, was found in the AC data.
Our approach to the treatment of the magnitude equation was a compromise between the statistical uncertainty of its determination by the conventional plate adjustment technique and the necessity to eliminate the effect, at least in the most prominent cases. The decision as to which type of plate model given by Eqs. (5) - with or without magnitude-dependent terms - should be adopted for each AC zone was made on the basis of two criteria: the size of the magnitude equation from the AC-Hipparcos residuals, and the comparison of the reduction quality estimates of the two plate models. It should be noted that the two criteria estimate the magnitude equation in distinct magnitude intervals: the comparison with Hipparcos provides information on bright stars, while the reduction quality estimates, being dominated by faint stars, estimate the magnitude equation at the faint end. If the introduction of the magnitude-dependent terms increased the reduction quality, or if a sizeable magnitude equation was found from the comparison with Hipparcos, the magnitude-dependent terms were adopted. The AC zones reduced by plate model (5) with the magnitude-dependent terms are checked in the last column of Table 2.
As can be seen (cf. Table 2), the values for the reduction quality estimates after the first step of the reduction procedure are always lower than those after the third step. This is due to the higher density of the ACRS Catalogue, which leads to smaller variances of the plate parameters and, thus, to smaller values of the reduction quality estimates. On the other hand, the better systematic quality of the reduction onto the ACRS system (as indicated by the smaller values for the reduction quality estimates) is limited to the scale of an AC plate, while on larger scales the systematic errors of the ACRS still persist. Using Hipparcos at the final step of the reduction ensures better systematic quality at the global scale, which is most important for many applications. However, it is achieved at the price of larger systematic errors on the scale of about one degree.
The reduction quality estimates and the rms scatter of the residuals represent two different attempts to assess the accuracy of the derived star positions. In the ideal case of an error-free reference catalogue and equal measurement errors of all stars, the two should coincide. In the real world, the reduction quality estimates may exceed the rms scatter or vise versa, depending on the actual balance between the reference catalogue errors, the plate model completeness and the presence of magnitude equation. The dominant role in both estimates is played by the random errors of the AC observations. However, the rms scatter of the residuals additionally reflects the reference catalogue errors. Accordingly, Table 2 shows that rms scatter with respect to Hipparcos is 1.5 times less than that with respect to ACRS. This is partly due to the superior quality of the Hipparcos proper motions, and partly to the higher correlation of the reduced AC positions of Hipparcos stars with the Hipparcos data. The latter is caused by the significantly smaller number of reference stars per plate.
Reduction quality estimates are based on all stars with two or more
observations, and thus these estimates of the accuracy of the reduced AC
measurements refer to faint stars. A test computation of ![]() and
and ![]() using only Tycho stars (which on average are about one magnitude brighter)
resulted in values which are about 30 per cent smaller than those given in
Table 2.
using only Tycho stars (which on average are about one magnitude brighter)
resulted in values which are about 30 per cent smaller than those given in
Table 2.
Copyright The European Southern Observatory (ESO)