Up: Atomic data from the
The Fe XVI target is represented by a 12-level approximation:
3s S1/2, 3p
S1/2, 3p P
P , 3p
, 3p P
P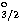 ,
,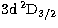 ,
,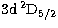 ,
, 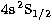 ,4p
,4p P
P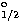 , 4p
, 4p P
P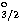 ,4d
,4d D3/2, 4d
D3/2, 4d D5/2,
4f
D5/2,
4f F
F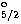 and
and 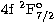 .The wavefunctions are obtained with the structure code
SUPERSTRUCTURE, originally developed by
Eissner
et al. (1974) and generalized by
Nussbaumer & Storey (1978). A summary of the
code's main features is given by Eissner (1991).
In this approach the wavefunctions are expressed in a configuration
expansion of the type
.The wavefunctions are obtained with the structure code
SUPERSTRUCTURE, originally developed by
Eissner
et al. (1974) and generalized by
Nussbaumer & Storey (1978). A summary of the
code's main features is given by Eissner (1991).
In this approach the wavefunctions are expressed in a configuration
expansion of the type
| 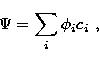 |
(23) |
where the basis functions 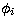 are constructed from one-electron
orbitals computed in a Thomas-Fermi-Dirac- Amaldi
statistical model potential
are constructed from one-electron
orbitals computed in a Thomas-Fermi-Dirac- Amaldi
statistical model potential 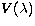 as described by
Eissner
& Nussbaumer (1975) for
as described by
Eissner
& Nussbaumer (1975) for 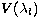 and
Nussbaumer & Storey (1978) for
and
Nussbaumer & Storey (1978) for 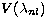 .The scaling parameters
.The scaling parameters 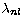 are computed variationally so as
to minimize the weighted sum of the non-relativistic term energies. The
are computed variationally so as
to minimize the weighted sum of the non-relativistic term energies. The
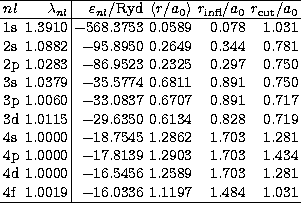
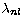 parameters for the present calculation are listed in
Table 1 along with other properties of the target orbitals. Of
particular relevance to the topping-up procedure
are the last point of inflection and the mean
radius of each orbital function. Tabulated radial functions
are input to Stage 1 of the R-matrix code. Beyond the radial distance
parameters for the present calculation are listed in
Table 1 along with other properties of the target orbitals. Of
particular relevance to the topping-up procedure
are the last point of inflection and the mean
radius of each orbital function. Tabulated radial functions
are input to Stage 1 of the R-matrix code. Beyond the radial distance
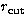 a Whittaker expansion can be employed
up to the R-matrix radius of 4.0 Bohr radii a0; there
the most diffuse orbital (4d) has decayed to relative magnitude 0.002.
a Whittaker expansion can be employed
up to the R-matrix radius of 4.0 Bohr radii a0; there
the most diffuse orbital (4d) has decayed to relative magnitude 0.002.
For the present system it is relatively easy to obtain an accurate
target representation. Internal consistency and comparison with previous
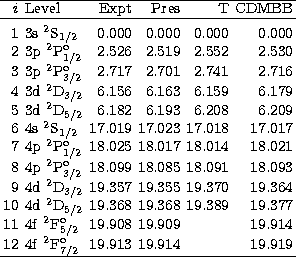
calculations and experiment (see Tables 2 and 3) suggest
an accuracy of the target level energies and f-values within the 2%
uncertainty range. Note that
levels 9 and 10 are labeled incorrectly in Table 2
of Tayal (1994),
whereas they are tabulated correctly in the present Table 2.
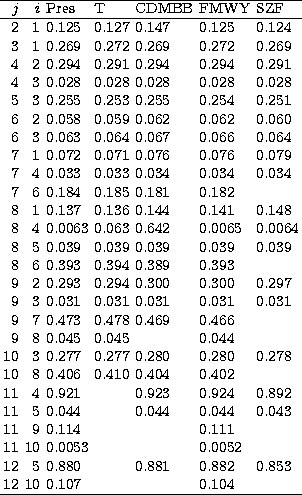
The reported computed oscillator strengths for the 4-8 transition
differ by up to a factor of 100. Varying the present 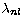 by as much as 10% would change our f-value of 0.0063 by not more than 20%
(while unbalancing the excellent agreement between length and velocity
results).
Besides, the present oscillator strength for this transition agrees closely
with
the measurement listed in Fuhr et al. (1981) and the theoretical value
obtained by Sampson et al. (1990). Other
differences with the calculation by
Cornille et al. (1997),
namely for transitions 1-2, 2-6, 3-6, 1-7 and 1-8 in
Table 3, are small, and they can be explained as the result of
alternative optimization procedures in SUPERSTRUCTURE such as different
weighting in the variational functional or fewer variational parameters
(perhaps
by as much as 10% would change our f-value of 0.0063 by not more than 20%
(while unbalancing the excellent agreement between length and velocity
results).
Besides, the present oscillator strength for this transition agrees closely
with
the measurement listed in Fuhr et al. (1981) and the theoretical value
obtained by Sampson et al. (1990). Other
differences with the calculation by
Cornille et al. (1997),
namely for transitions 1-2, 2-6, 3-6, 1-7 and 1-8 in
Table 3, are small, and they can be explained as the result of
alternative optimization procedures in SUPERSTRUCTURE such as different
weighting in the variational functional or fewer variational parameters
(perhaps 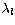 rather than
rather than 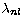 ).
).
Table 1:
Properties of the Fe XVI target orbitals:
binding energy in the potential 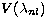 , mean radius, last point
of inflection (both after Schmidt orthogonalization) and cut-off radius of
SUPERSTRUCTURE output
, mean radius, last point
of inflection (both after Schmidt orthogonalization) and cut-off radius of
SUPERSTRUCTURE output
|
|
Table:
Comparison of computed absorption oscillator strengths fij
(length formulation) for the Fe XVI target.
Pres: present results. T: Tayal (1994);
CDMBB: Cornille et al. (1997); FMWY: Fuhr et al. (1981);
SZF: Sampson et al. (1990).
Hutton et al. (1988) give experimental values for the first two
entries:
0.115 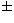 0.007 and 0.244
0.007 and 0.244 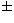 0.015
0.015
|
|


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)
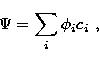
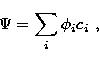
![]() by as much as 10% would change our f-value of 0.0063 by not more than 20%
(while unbalancing the excellent agreement between length and velocity
results).
Besides, the present oscillator strength for this transition agrees closely
with
the measurement listed in Fuhr et al. (1981) and the theoretical value
obtained by Sampson et al. (1990). Other
differences with the calculation by
Cornille et al. (1997),
namely for transitions 1-2, 2-6, 3-6, 1-7 and 1-8 in
Table 3, are small, and they can be explained as the result of
alternative optimization procedures in SUPERSTRUCTURE such as different
weighting in the variational functional or fewer variational parameters
(perhaps
by as much as 10% would change our f-value of 0.0063 by not more than 20%
(while unbalancing the excellent agreement between length and velocity
results).
Besides, the present oscillator strength for this transition agrees closely
with
the measurement listed in Fuhr et al. (1981) and the theoretical value
obtained by Sampson et al. (1990). Other
differences with the calculation by
Cornille et al. (1997),
namely for transitions 1-2, 2-6, 3-6, 1-7 and 1-8 in
Table 3, are small, and they can be explained as the result of
alternative optimization procedures in SUPERSTRUCTURE such as different
weighting in the variational functional or fewer variational parameters
(perhaps ![]() rather than
rather than ![]() ).
).