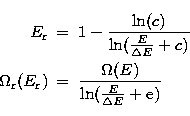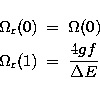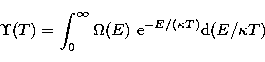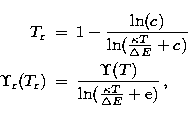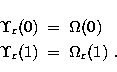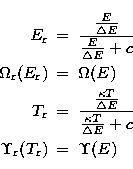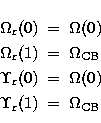Up: Atomic data from the
Subsections
In this work physical processes are described by the Hamiltonian
| 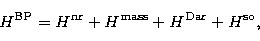 |
(1) |
where Breit-Pauli (BP) contributions of order 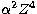 Ry are added
to the non-relativistic Hamiltonian
Ry are added
to the non-relativistic Hamiltonian 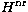 ; namely the mass-velocity,
one-body Darwin and ordinary spin-orbit terms. The
two-body components of relative BP-order 1/Z are neglected, which is adequate
in our case. Each term of (1) involves N target electrons
and a colliding electron, and
; namely the mass-velocity,
one-body Darwin and ordinary spin-orbit terms. The
two-body components of relative BP-order 1/Z are neglected, which is adequate
in our case. Each term of (1) involves N target electrons
and a colliding electron, and 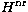 includes a central potential due
to an atomic nucleus with charge number Z.
Thus expression (1) can be expanded in terms of
states of total angular momentum and parity
includes a central potential due
to an atomic nucleus with charge number Z.
Thus expression (1) can be expanded in terms of
states of total angular momentum and parity 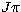 when taking the entire Hamiltonian, and of states of total spin, orbital
angular
momentum
and parity
when taking the entire Hamiltonian, and of states of total spin, orbital
angular
momentum
and parity 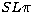 when the contribution
when the contribution 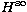 is neglected.
We examine results obtained in either of these coupling schemes; they are
connected by vector-coupling and term-coupling coefficients (TCC) and the
transformation can be carried out at different stages of the calculation.
This in turn affects computer time and accuracy.
is neglected.
We examine results obtained in either of these coupling schemes; they are
connected by vector-coupling and term-coupling coefficients (TCC) and the
transformation can be carried out at different stages of the calculation.
This in turn affects computer time and accuracy.
When collision-type trial functions
(Burke & Seaton 1971) are used, the wavefunction for
the total system of target and colliding electron is given by the expansion
| 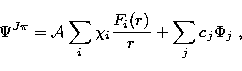 |
(2) |
where 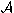 is the antisymmetrization operator,
is the antisymmetrization operator, 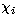 are vector
coupled products of the target eigenfunctions and the angular part of
the incident-electron functions, and the Fi(r) are the radial parts of
the latter. The functions
are vector
coupled products of the target eigenfunctions and the angular part of
the incident-electron functions, and the Fi(r) are the radial parts of
the latter. The functions 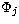 are bound-type functions of the total system
introduced to
compensate for orthogonality conditions imposed on the Fi(r) and to
render short-range correlations. The Kohn variational principle yields
coupled integro-differential (ID) equations for the radial
functions Fi(r) for each angular symmetry.
are bound-type functions of the total system
introduced to
compensate for orthogonality conditions imposed on the Fi(r) and to
render short-range correlations. The Kohn variational principle yields
coupled integro-differential (ID) equations for the radial
functions Fi(r) for each angular symmetry.
R-matrix techniques (Burke et al. 1971;
Berrington et al. 1974, 1978) are employed to solve the
ID equations inside the R-matrix box (for 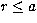 , say).
, say).
One way to take relativistic effects into account is to employ the BP
extensions which were first introduced in the R-matrix method
by Scott & Burke (1980) and
Scott & Taylor (1982). The target Hamiltonian
is diagonalized in intermediate coupling. We make use of the resulting TCCs
when recoupling the prior systems with respective 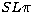 symmetries to
symmetries to
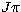 symmetries,
and we add the spin-orbit contribution from
symmetries,
and we add the spin-orbit contribution from 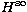 due to the
colliding electron.
due to the
colliding electron.
To match to physical asymptotic boundary conditions
a pair coupling scheme is adopted where the
target angular momentum j is added to the orbital angular momentum l and
spin s of the incident electron through an
intermediate quantum number K (see, for example, Saraph 1972):
| 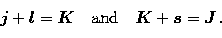 |
(3) |
Since spin-orbit coupling is negligible when 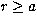 ,no kinetic effects enter between the auxiliary states K and total
angular momentum J. We make use of this fact when deriving
expressions for contributions from high angular momenta.
,no kinetic effects enter between the auxiliary states K and total
angular momentum J. We make use of this fact when deriving
expressions for contributions from high angular momenta.
The other recipe, computationally cheaper, is to first solve the
coupled ID equations in the collisional 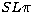 symmetry. Then,
following Saraph (1978), collision
strengths between fine-structure levels are obtained by algebraic recoupling of
the scattering matrices from LS to pair coupling. The method allows
for term mixing via TCCs.
So the relativistic effect of
term mixing through spin-orbit interaction is obtained.
However channel energies are
degenerate for fine-structure levels associated with the same term.
This approach will be referred to as the TCC method.
symmetry. Then,
following Saraph (1978), collision
strengths between fine-structure levels are obtained by algebraic recoupling of
the scattering matrices from LS to pair coupling. The method allows
for term mixing via TCCs.
So the relativistic effect of
term mixing through spin-orbit interaction is obtained.
However channel energies are
degenerate for fine-structure levels associated with the same term.
This approach will be referred to as the TCC method.
The asymptotic region (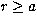 ) is treated by
the perturbative method described by Seaton (1985) and
Berrington et al. (1987). In this region the ID
equations reduce to the ordinary coupled differential equations
) is treated by
the perturbative method described by Seaton (1985) and
Berrington et al. (1987). In this region the ID
equations reduce to the ordinary coupled differential equations
| 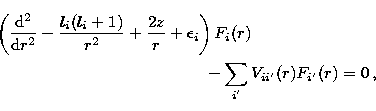 |
|
| (4) |
where z=Z-N is the residual charge of the ion,
li and 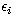 are the channel orbital
angular momentum and energy of the colliding electron (in Rydberg units)
and the quantities Vii' are long-range multipole potentials.
Since asymptotically
|Vii'(r)|
are the channel orbital
angular momentum and energy of the colliding electron (in Rydberg units)
and the quantities Vii' are long-range multipole potentials.
Since asymptotically
|Vii'(r)| 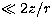 , these potentials can be treated by perturbation
techniques. The asymptotic codes devised for the IP work allow for two options.
Option 1: the potentials Vii' are
included to first order, and Option 0: the potentials Vii' are neglected.
Since
computations with Option 0 are considerably less time consuming, we
investigate its range of validity.
, these potentials can be treated by perturbation
techniques. The asymptotic codes devised for the IP work allow for two options.
Option 1: the potentials Vii' are
included to first order, and Option 0: the potentials Vii' are neglected.
Since
computations with Option 0 are considerably less time consuming, we
investigate its range of validity.
The high-l contribution to the collision strength (top-up)
for optically allowed (oa)
transitions is computed for 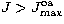 with a procedure based on
the Coulomb-Bethe approximation (Burgess 1974) and formulated by
Burke & Seaton (1986) in the context of the R-matrix
coding.
with a procedure based on
the Coulomb-Bethe approximation (Burgess 1974) and formulated by
Burke & Seaton (1986) in the context of the R-matrix
coding.
| ![\begin{eqnarray}
\sum_{l=\lambda+1}\sp\infty\Omega_{l,l-1}+\Omega_{l-1,l}=\biggl...
...\lambda-1,\lambda}\biggr]\bigg/
\bigl[\epsilon_1-\epsilon_2\bigr]\end{eqnarray}](/articles/aas/full/1999/08/ds8187/img23.gif) |
|
| (5) |
where 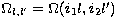 .The formulation requires just two partial collision strengths
for each dipole allowed transition (i1,i2)
at some
.The formulation requires just two partial collision strengths
for each dipole allowed transition (i1,i2)
at some 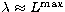 (n.b. i stands for
(n.b. i stands for
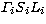 and
and 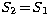 for these transitions).
This procedure has been extended to intermediate coupling and details will be
published elsewhere.
For non-allowed (na) transitions we approximate the top-up for
for these transitions).
This procedure has been extended to intermediate coupling and details will be
published elsewhere.
For non-allowed (na) transitions we approximate the top-up for
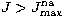 with a geometric series.
Here
with a geometric series.
Here 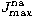 is the highest J-value for which the ID equations
are solved.
is the highest J-value for which the ID equations
are solved.
In order to assess the convergence of the partial wave expansion
the resulting collision strengths are analyzed by means of the scaling
techniques developed by Burgess & Tully (1992).
The collision strength 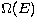 is mapped onto the reduced form
is mapped onto the reduced form
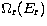 , where the infinite energy range is scaled
to the finite interval (0,1). For an allowed transition the
scaled parameters
, where the infinite energy range is scaled
to the finite interval (0,1). For an allowed transition the
scaled parameters 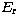 and
and 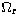 are the
dimensionless quantities
are the
dimensionless quantities
| 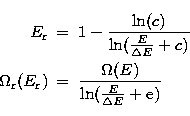 |
(6) |
| (7) |
with 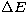 being the transition energy, E the electron energy
with respect to the reaction threshold and c is an adjustable scaling
parameter. A key aspect of the approach by Burgess & Tully lies in the fact
that the low as well as the high energy limits
being the transition energy, E the electron energy
with respect to the reaction threshold and c is an adjustable scaling
parameter. A key aspect of the approach by Burgess & Tully lies in the fact
that the low as well as the high energy limits
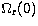 and
and 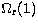 are both finite
and can be computed. For an electric dipole transition these limits are
are both finite
and can be computed. For an electric dipole transition these limits are
| 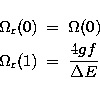 |
(8) |
| (9) |
where gf is the weighted oscillator strength (gf-value) for the
transition. This method
can also be extended to treat the effective collision strength
| 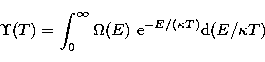 |
(10) |
through the analogous relations
| 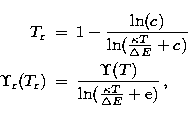 |
(11) |
| (12) |
where T is the electron temperature and 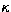 the Boltzmann constant;
the limits are
the Boltzmann constant;
the limits are
| 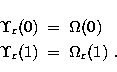 |
(13) |
| (14) |
For a forbidden transition similar scaling relations are introduced by
| 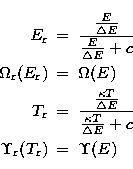 |
(15) |
| (16) |
| (17) |
| (18) |
with the following limits
| 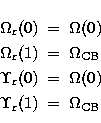 |
(19) |
| (20) |
| (21) |
| (22) |
where 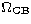 is the Coulomb-Born high-energy limit.
is the Coulomb-Born high-energy limit.


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)
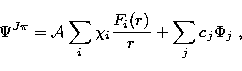
![]() , say).
, say).
![]() symmetries to
symmetries to
![]() symmetries,
and we add the spin-orbit contribution from
symmetries,
and we add the spin-orbit contribution from ![]() due to the
colliding electron.
due to the
colliding electron.
![]() symmetry. Then,
following Saraph (1978), collision
strengths between fine-structure levels are obtained by algebraic recoupling of
the scattering matrices from LS to pair coupling. The method allows
for term mixing via TCCs.
So the relativistic effect of
term mixing through spin-orbit interaction is obtained.
However channel energies are
degenerate for fine-structure levels associated with the same term.
This approach will be referred to as the TCC method.
symmetry. Then,
following Saraph (1978), collision
strengths between fine-structure levels are obtained by algebraic recoupling of
the scattering matrices from LS to pair coupling. The method allows
for term mixing via TCCs.
So the relativistic effect of
term mixing through spin-orbit interaction is obtained.
However channel energies are
degenerate for fine-structure levels associated with the same term.
This approach will be referred to as the TCC method.
![]() ) is treated by
the perturbative method described by Seaton (1985) and
Berrington et al. (1987). In this region the ID
equations reduce to the ordinary coupled differential equations
) is treated by
the perturbative method described by Seaton (1985) and
Berrington et al. (1987). In this region the ID
equations reduce to the ordinary coupled differential equations
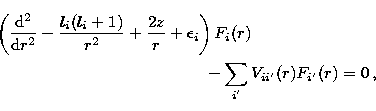
![]() with a procedure based on
the Coulomb-Bethe approximation (Burgess 1974) and formulated by
Burke & Seaton (1986) in the context of the R-matrix
coding.
with a procedure based on
the Coulomb-Bethe approximation (Burgess 1974) and formulated by
Burke & Seaton (1986) in the context of the R-matrix
coding.
![\begin{eqnarray}
\sum_{l=\lambda+1}\sp\infty\Omega_{l,l-1}+\Omega_{l-1,l}=\biggl...
...\lambda-1,\lambda}\biggr]\bigg/
\bigl[\epsilon_1-\epsilon_2\bigr]\end{eqnarray}](/articles/aas/full/1999/08/ds8187/img23.gif)
![]() is mapped onto the reduced form
is mapped onto the reduced form
![]() , where the infinite energy range is scaled
to the finite interval (0,1). For an allowed transition the
scaled parameters
, where the infinite energy range is scaled
to the finite interval (0,1). For an allowed transition the
scaled parameters ![]() and
and ![]() are the
dimensionless quantities
are the
dimensionless quantities