In this section we present a small sample of the fine structure collision strengths in three different approximations: (a) 19BP, (b) 8CC, and (c) 34CC, and compare their Maxwellian-averaged collision strengths (the term coupling results, 8CC+TCC, are not considered as they are found to be nearly identical with the NR 8CC results).
The extensive resonance structures are displayed in Figs. 1 for the
collision strengths for the first transition ![]() .As mentioned in the previous section, the mesh is considerably more
refined in the low energy region E < 0.25 Rydberg, than at higher energies,
so as to resolve accurately the near threshold resonances. The 8CC and
the 34CC calculations assume degenerate fine structure level energies
belonging to a given LS term, whereas the 19BP calculation employs
observed energies. The 19BP results in Fig. 1a differ in detail from the
8CC and the 34CC results (Figs. 1b,c) , both of which are very nearly the same,
as expected for low-lying transitions; the differences are only expected
to manifest themselves at higher energies owing to additional target
states in the larger 34CC calculation. Figures 1b and 1c are nearly
identical up to about 0.4 Rydberg. The 19BP calculations show
significantly different positions and shapes for the individual
features. The dense resonance structures and the background
collision strengths appear consistent, so except at the low
temperatures where there is no abundance of Fe VI in astronomical
objects and transitions between very high-lying levels
the averaged collision strengths
are almost not influenced by relativistic effects, as seen from
the comparisons in Tables 2 and 3 (described below).
.As mentioned in the previous section, the mesh is considerably more
refined in the low energy region E < 0.25 Rydberg, than at higher energies,
so as to resolve accurately the near threshold resonances. The 8CC and
the 34CC calculations assume degenerate fine structure level energies
belonging to a given LS term, whereas the 19BP calculation employs
observed energies. The 19BP results in Fig. 1a differ in detail from the
8CC and the 34CC results (Figs. 1b,c) , both of which are very nearly the same,
as expected for low-lying transitions; the differences are only expected
to manifest themselves at higher energies owing to additional target
states in the larger 34CC calculation. Figures 1b and 1c are nearly
identical up to about 0.4 Rydberg. The 19BP calculations show
significantly different positions and shapes for the individual
features. The dense resonance structures and the background
collision strengths appear consistent, so except at the low
temperatures where there is no abundance of Fe VI in astronomical
objects and transitions between very high-lying levels
the averaged collision strengths
are almost not influenced by relativistic effects, as seen from
the comparisons in Tables 2 and 3 (described below).
Figures 2 present further examples of resonances in other
transition ![]() within the ground term.
One main feature is highlighted. In Figs. 2a-c
the near-threshold region is full of dense resonances as in
Figures 1, but the elevated background at low energies E < 0.25 Rydbergs
is more pronounced relative to higher energies. The reason for the
high density of resonances in this low energy range is the presence of a
number of closely spaced thresholds (Table 1) that give rise to several
overlapping Rydberg series of resonances.
within the ground term.
One main feature is highlighted. In Figs. 2a-c
the near-threshold region is full of dense resonances as in
Figures 1, but the elevated background at low energies E < 0.25 Rydbergs
is more pronounced relative to higher energies. The reason for the
high density of resonances in this low energy range is the presence of a
number of closely spaced thresholds (Table 1) that give rise to several
overlapping Rydberg series of resonances.
The dominant role of resonances is clear, particularly compared to the
two earlier calculations by Nussbaumer & Storey (1978) and
Garstang et al. (1978), which correspond only to the non-resonant
background. The Nussbaumer and Story calculations were in DW
approximation that does not enable a treatment of resonances.
However, the Garstang et al.
calculations were in the close coupling approximation using a small
basis set (Garstang et al. 1978),
but they did not obtain the resonance structures and
presented only averaged values (these are denoted as
asterisks near the threshold energy).
The computed rate coefficients are higher by several factors in
comparision with the earlier collision strengths. For example, the rate
coeffcient for the transition ![]() (Table
1, first transition) is approximately a factor of 5 higher (at 20 000 K) than the
previous collision strengths shown in Fig. 1c. For the
(Table
1, first transition) is approximately a factor of 5 higher (at 20 000 K) than the
previous collision strengths shown in Fig. 1c. For the ![]() transition the differences with previous data are about a
factor of 7.
transition the differences with previous data are about a
factor of 7.
Because of the larger target expansion in the 34CC case (as shown in Fig. 7 of CP), there are more extensive resonance structures in the 34CC case compared to the 19BP or the 8CC case at high impact energies. Consequently, as seen below, the 34CC rate coefficients should show a larger resonance enhancement especially at high electron temperatures.
The procedure for obtaining the Maxwellian-averaged collision strength, or the
effective collision strength, can be found in earlier publications
in this series (e.g. see Papers I, VI or XVIII). This quantity is defined
as
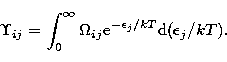 |
(1) |
![\begin{figure}
\includegraphics [width=8.8cm,clip]{fig3.ps}\end{figure}](/articles/aas/full/1999/08/ds1659/Timg44.gif) |
Figure 3:
The collision strengths
enhanced by CBe top-up for the
optically allowed transitions
a) |
Figures 3 show the collision strengths for the optically allowed transitions
(a) ![]() ,(b)
,(b) ![]() ,(c)
,(c) ![]() ,and (d)
,and (d) ![]() .As mentioned earlier, the Coulomb-Bethe approximation was employed
to estimate the contributions from high partial waves.
It is clear from
the figures that relative resonance contributions are not
as strong as in the forbidden transitions and the rate coefficients
are dominated by the high energy region where the collision strength
has the Bethe asymptotic behavior,
.As mentioned earlier, the Coulomb-Bethe approximation was employed
to estimate the contributions from high partial waves.
It is clear from
the figures that relative resonance contributions are not
as strong as in the forbidden transitions and the rate coefficients
are dominated by the high energy region where the collision strength
has the Bethe asymptotic behavior, ![]() .
.
As discussed in detail in the earlier work by CP on the bound channel
expansion in the close coupling calculations for Fe VI, these (N+1)-electron
functions are found to appear as resonances in the collision strengths.
Often in close coupling calculations the bound channel configurations
are not well represented from the point of view of a reasonably complete
configuration-interaction expansion. This is particularly the case when
the continuum channel expansion over the target states does not include
the same configurations as the bound channels, which can then lead to
large pseudoresonances in the cross sections. However, if care is
exercised in the choice of the continuum and the bound channel
expansions, the latter set corresponds well to physical resonances.
For example, CP find that one particular bound channel configuration
![]() leads to a considerable but diffuse rise in the near-threshold
background of the collision strength
leads to a considerable but diffuse rise in the near-threshold
background of the collision strength
![]() and
and ![]() (Figs. 6a,b of CP are plotted with and without this configuration).
We also note that such bound channel resonances were also found to have
an appreciable effect in the near-threshold region in an
earlier work on the photoionization of Fe IV
(Bautista & Pradhan 1997).
(Figs. 6a,b of CP are plotted with and without this configuration).
We also note that such bound channel resonances were also found to have
an appreciable effect in the near-threshold region in an
earlier work on the photoionization of Fe IV
(Bautista & Pradhan 1997).
The Maxwellian-averaged collision strengths were calculated for all 3610 non-vanishing transitions between 80 energy levels shown in Table 4 (available in electronic form) for 21 temperatures ranging from 10 000 to 100 0000 K.
Copyright The European Southern Observatory (ESO)