2 Atomic calculations

The target expansions in the present work are based on the 34-term wave function expansion for Fe VI developed by Bautista (1996) using the SUPERSTRUCTURE program in his non-relativistic calculations for photoionization cross sections of Fe V. The SUPERSTRUCTURE calculations for Fe VI were extended to include relativistic fine structure using the Breit-Pauli Hamiltonian (Eissner et al. 1974; Eissner 1998). 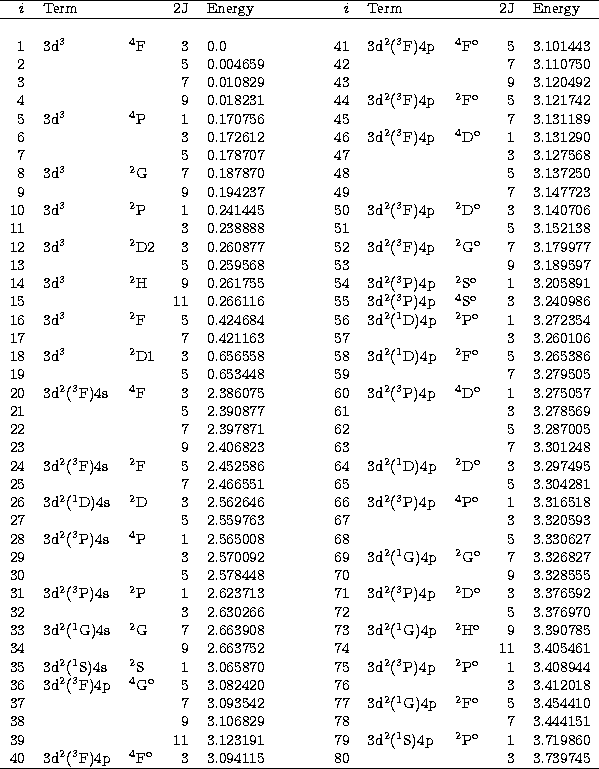The designations for the 80 levels (34 LS terms) dominated by the configurations $3{\rm d}^3$, $3{\rm d}^24{\rm s}$ and $3{\rm d}^24$p and their observed energies (Sugar & Corliss 1985), are shown in Table 1. These observed energies were used in the scattering Hamiltonian diagonalization to obtain the surface amplitudes at stage STGH (Berrington et al. 1995). This table also provides the key to the level indices for transitions in tabulating the Maxwellian-averaged collision strengths. The subset of 19-levels, the first 8 LS terms dominated by $3{\rm d}^3$, are used in both the intermediate coupling BP and the non-relativistic recoupling calculations, with and without the term coupling coefficients (TCC's) for the purpose of comparisons (Chen & Pradhan 1998, CP). An indication of the accuracy of the target eigenfunctions may be obtained from the calculated energy levels in Table 1 of CP and from the computed length and velocity oscillator strengths for some of the dipole fine structure transitions given in Table 2 of CP. The agreement between the length and velocity oscillator strengths is generally about 10%, an acceptable level of accuracy for a complex iron ion.

  

Table 1: The 80 fine structure levels corresponding to the 34 LS terms included in the calculations and their observed energies (Ry) in Fe VI (Sugar & Corliss 1985)

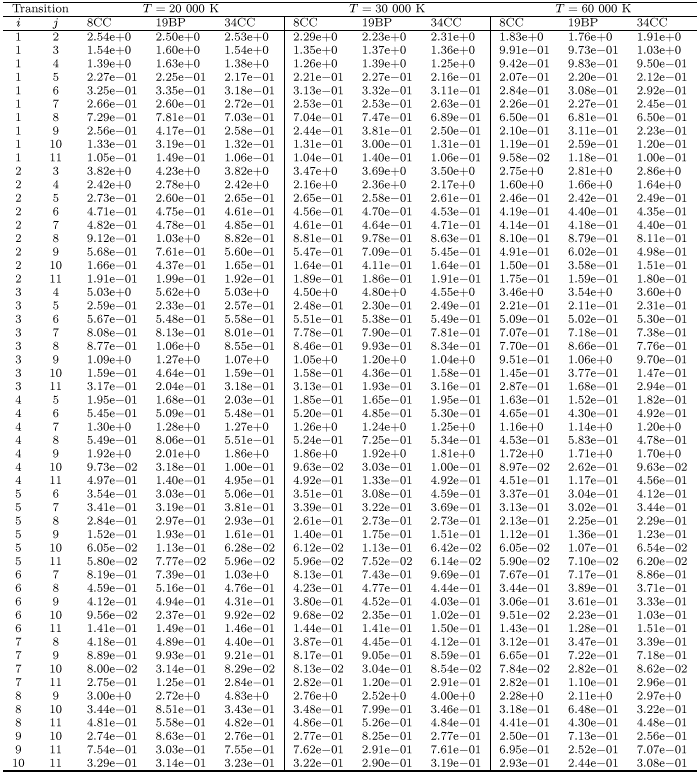
The collision calculations in the present work, as in the earlier works in Papers III, VI, XVIII and XXVII of the IP, entail the calculation of the reactance matrix (the K-matrix) which yields the collision strengths. In the NR algebraic recoupling approach, the K-matrices are obtained as usual by the different stages of the R-matrix package (Berrington et al. 1995) in LS coupling. The  K-matrices are subsequently transformed from LS coupling to pair coupling (Saraph 1972, 1978), using the STGFJ code (Luo & Pradhan 1990; Zhang & Pradhan 1995a) which is an extension of the NR LS coupling asymptotic region code, STGF (Hummer et al. 1993). The collision strengths were calculated for a large number of electron energies ranging from 0 to 10 Rydbergs by 34CC. This energy range was carefully chosen in order to obtain detailed structures of collision strengths in the region where they are dominated by resonances, as well as in an extended region where resonances are not important or have not been included but which are necessary to obtain accurate Maxwellian-averaged rate coefficients for the electron temperature range of interest. As the electron Maxwellian at a given temperature is weighted towards lower energies, it is desirable and usually necessary to use a fine mesh of energies in the near-threshold region. The mesh is coarser at higher energies not only because it is weighted less in rate coefficients, but also because the calculations are more CPU time consuming as more target thresholds are accessible resulting in a higher number of open channels than at low energies.

In order to delineate the extensive near-threshold resonance structures, an effective quantum number $\nu$-mesh was used to obtain the collision strengths at 8913 energy points in the range E = 0 - 0.25 Rydbergs. On this so called "quantum defect'' mesh, 100 points ($\Delta\nu=0.01$) are obtained in each interval ($\nu$, $\nu +1)$.The $\nu$-mesh ensures equal sampling of resonances in each successive interval, $(\nu$, $\nu~+~1)$ where $\nu (E)=z/\sqrt{E_{\rm t}-E}$; $E_{\rm t}$ is the energy of the particular target threshold to which the resonance series converges. In the energy region E = 0.25 - 10 Rydbergs, a constant energy mesh was used. A practical reason for terminating the $\nu$-mesh at 0.25 Rydberg is that it would take considerably more computing time and memory resources, owing to a large number of additional open channels at higher energies. The calculations are therefore optimised so as to obtain extensive delineation of resonances for the collision strengths for forbidden transitions in the low energy region that contributes predominantly to the Maxwellian rate coefficient. For the optically allowed transitions, the dominant contribution may arise from higher partial waves and higher energy regions since $\Omega \sim \ln (\epsilon$) where resonances are relatively less important.

It is convenient to divide the overall calculation into groups of total (e + ion) symmetries $SL\pi$ according to their multiplicity, i.e. (2S+1) = 1,3, and 5 (L and S are the corresponding total orbital and spin angular momenta). Following algebraic calculations at the R-matrix STG2 stage in LS coupling, the $SL\pi$ symmetries are then recoupled in the program RECUPD to obtain total $J\pi$ (where J=L+S). At low impact electron energies, especially for forbidden transitions between the low-lying levels in Fe VI, contributions to the collision strengths from total symmetries $J\pi$ with small J are dominant and those from large J are negligible. We calculated partial wave contributions from total angular momenta of the (e + ion) system with J = 0 - 15. The corresponding SL's (for both even and odd parities) included are

$0\ \le \ L \ \le 15,\ (2S+1)\ =\ 1$

$0\ \le \ L \ \le 16,\ (2S+1)\ =\ 3$

$0\ \le \ L \ \le 17,\ (2S+1)\ =\ 5.$

The sum over the symmetries included should be sufficient to ensure convergence of the total collision strengths for most of the non-dipole transitions. As in several earlier calculations (e.g. for Fe IV, Zhang & Pradhan 1995a), Coulomb-Bethe (CBe) approximation was employed to account for the large $\ell$contributions to supplement the collision strengths for optically allowed transitions in the energy range 0-10 Rydbergs. As the ion abundance peak of Fe VI in stellar sources is at the temperature 200 000 K (Arnaud & Rothenflug 1985), the collision strengths were calculated for energy range 10-100 Rydbergs or so for optically allowed transitions by CBe approach and for forbidden transitions by linking a tail with $1/\epsilon$ decrease in collision strengths. The electric dipole fine structure oscillator strengths required for CBe top-up were obtained from the BP SUPERSTRUCTURE calculations (as given in Table 2 of CP for selected transitions).

  

Table 2: Comparison of the effective collision strengths $\Upsilon_{ij} (T)$ at 3 temperatures which cover the abundance of Fe VI in photoionized H II regions, from the 8CC calculation, the 19BP calculation and the 34CC calculation. i and j, referred to Table 1, are the initial and final levels

At the STG2 stage of the R-matrix calculations, it is required to specify the (N+1)-electron configurations that constitute the bound channel terms ${\Phi_j}$'s in the wave function expansion. However, the computer time and memory of the calculation are dependent on the number of such configurations included. A judicious choice needs to be made depending on whether any given particular configuration is important in the calculations or not. Therefore, in addition to those configurations required by the orthogonality condition between the continuum orbitals and the bound target orbitals, a number of complete trial calculations were carried out to select the full set of bound channel configurations employed in the present calculations. Especially, those configurations with open 3p subshell ($\rm 3p^4$ or $\rm 3p^5$) have noticeably influence on the results (the very broad near-threshold resonance features). Table 3 of CP lists these configurations according to even and odd parity. The earlier CP paper also gives a discussion of the bound channel configurations and associated resonance structures.

  

Table 3: Comparison of the effective collision strengths $\Upsilon_{ij} (T)$ at 3 temperatures which cover the peak abundance of Fe VI in coronal plasmas sources, from the 8CC calculation, the 19BP calculation and the 34CC calculation. i and j, referred to Table 1, are the initial and final levels